V. Сабақты қорытындылау. Сынып геометрия пәнінен І жарты жылдыққа арналған күнтізбелік жоспар
Сынып геометрия пәнінен І жарты жылдыққа арналған күнтізбелік жоспар
(Аптасына 2 сағат. Барлығы 34 сағат. Оқулық авторы И.Бекбоев)
| № | Сабақтың тақырыбы | Сағат саны | Күні |
| І. Төртбұрыштар (22 сағат) | |||
| Төртбұрыштар туралы түсінік. Төртбұрыштардың ішкі бұрыштарының қосындысы. | |||
| 2,3 | Параллелограмм және оның қасиеттері | ||
| 4,5 | Параллелограмм белгілері | ||
| Тіктөртбұрыш және оның қасиеттері | |||
| Ромб және оның қасиеттері | |||
| Квадрат | |||
| Бақылау жұмысы | |||
| 10,11 | Фалес теоремасы | ||
| 12,13 | Үшбұрыштың орта сызығы | ||
| 14,15 | Трапеция | ||
| 16,17 | Трапецияның орта сызығы | ||
| Пропорционал кесінділер | |||
| 19,20 | Үшбұрыштың тамаша нүктелері | ||
| Есептер шығару | |||
| Бақылау жұмысы | |||
| ІІ. Пифагор теоремасы (22 сағат) | |||
| 23,24 | Тікбұрышты үшбұрыштың сүйір бұрышының синусы, косинусы, тангенсі | ||
| Тест жұмысы | |||
| 26,27 | Негізгі тригонометриялық тепе – теңдіктер | ||
| 28-30 | Пифагор теоремасы | ||
| 31,32 | 300,450,600 бұрыштары үшін синус, косинус, тангенс, тригонометриялық функцияларының мәні | ||
| Тікбұрышты үшбұрыштың қабырғалары мен бұрыштарының арасындағы қатыстар | |||
| Бақылау жұмысы |
1 – сабақ
Сабақтың тақырыбы:Төртбұрыштар туралы түсінік. Төртбұрыштардың
ішкі бұрыштарының қосындысы.
Сабақтың мақсаты:
1. Білімділік:Төртбұрыш анықтамасы, оның элементтерін білу,
дөңес және дөңес емес төртбұрышты білу, төртбұрыштың ішкі
бұрыштарының қосындысын тұжырымдайтын теоремасын
білу, дәлелдей білу.
2. Дамытушылық:Оқушылардың ойлау қабілетін, өз бетімен еңбектену сезімдерін, білімдерін дамыту.
3. Тәрбиелік: Оқушыларды адалдыққа, шапшаңдыққа, өз бетімен еңбектенуге тәрбиелеу.
Сабақтың түрі: Жаңа білімді меңгерту.
Оқыту әдістері:Ауызша баяндау, сұрақ-жауап алу, есептер шығару.
Сабақтың көрнекілігі:Интерактивті тақта
Сабақтың барысы:1) Ұйымдастыру кезеңі
2) Қайталау
3) Жаңа сабақты меңгерту
4) Жаңа сабақты бекіту
5) Сабақты қорытындылау
6) Үйге тапсырма
II. Қайталау.
1) Жазықтықтың негізгі геометриялық фигураларын атаңдар.
2) Нүктелер мен түзулер қалай белгіленеді?
3) Үшбұрыш анықтамасы.
4) Үшбұрыштың периметрі
5) Үшбұрыштың ішкі бұрыштарының қосындысы.
III. Жаңа сабақ.
Анықтама. Әрбір үшеуі бір түзуде жатпайтын төрт нүктеден және оларды тізбектей қосатын қиылыспайтын төрт кесіндіден және сол кесінділермен шектелген жазықтықтың бөлігінен тұратын фигураны төртбұрыш деп атайды.
Берілген нүктелер төртбұрыштың төбелері, ал оларды қосатын кесінділер төртбұрыштың қабырғалары деп аталады.
Интерактивті тақтадан көрсетемін.
Слайд
Мына фигуралардың әрқайсысы төрт нүктеден және оларды тізбектей қосатын төрт кесіндіден тұрады. Осы фигуралардың қайсысы төртбұрыш болып табылады?
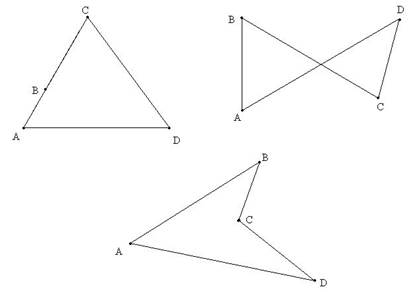
Төртбұрыштың элементтеріне интерактивті тақтадан мына кестені көрсете отырып анықтама беремін.
Слайд
| Төртбұрыш және оның элементтері. | |
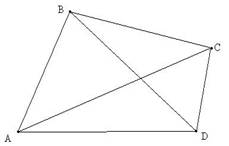 | АВ мен ВС, ВС мен СД, СД мен АД, АД мен АВ кесінділері бір түзудің бойында жатпайды; АВ мен СД, ВС мен АД кесінділері бір-бірімен қиылыспайды; А,В,С,Д нүктелері төртбұрыштың төбелері; А мен В, В мен С, С мен Д, Д мен А – көршілес төбелері; В мен Д, С мен А қарсы төбелері; АВ, ВС, СД, ДА кесінділері – төртбұрыштың қабырғалары; АВ мен ВС, ВС мен СД, СД мен ДА, ДА мен АВ кесінділері – көршілес қабырғалары; АВ мен СД, ВС мен АД – қарама-қарсы қабырғалары; АС мен ВД кесінділері – диагональдар;  АВС, АВС,  ВСД, ВСД,  СДА, СДА,  ДАВ – төртбұрыштың бұрыштары; Р=АВ + ВС + СД + ДА периметрі; АВСД, ВСДА, СДАВ, ДАВС – төртбұрыштың белгіленуі ДАВ – төртбұрыштың бұрыштары; Р=АВ + ВС + СД + ДА периметрі; АВСД, ВСДА, СДАВ, ДАВС – төртбұрыштың белгіленуі |
Төртбұрыштар дөңес және дөңес емес болып бөлінеді
Слайдтан көрсетіліп, анықтамасы айтылады.
Слайд.
| Төртбұрыштың түрлері | |
| Дөңес төртбұрыш | Дөңес емес төртбұрыштар |
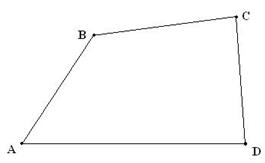 1) Қабырғасын қамтитын әр түзумен шектелген жарты жазықтықтың тек біреуінде ғана жатса, дөңес төртбұрыш болады. 2) Егер төртбұрыштың диогональдары қиылысса, төртбұрыш дөңес болады. 1) Қабырғасын қамтитын әр түзумен шектелген жарты жазықтықтың тек біреуінде ғана жатса, дөңес төртбұрыш болады. 2) Егер төртбұрыштың диогональдары қиылысса, төртбұрыш дөңес болады. | 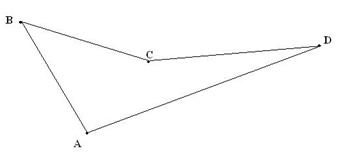 1) Төртбұрыш қабырғасын қамтитын кемінде бір түзумен шектелген жарты жазықтықтардың екеуінде де жатса, дөңес емес төртбұрыш болады. 2) Егер төртбұрыштың диогональдары қиылыспаса, төртбұрыш дөңес емес болады. 1) Төртбұрыш қабырғасын қамтитын кемінде бір түзумен шектелген жарты жазықтықтардың екеуінде де жатса, дөңес емес төртбұрыш болады. 2) Егер төртбұрыштың диогональдары қиылыспаса, төртбұрыш дөңес емес болады. |
Теорема.Төртбұрыштардың ішкі бұрыштардың қосындысы 360 º -қа тең.
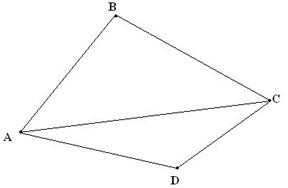
Берілгені: АВСД төртбұрыш.
Дәлелдеу керек :  А+
А+  В+
В+  С+
С+  Д =360º
Д =360º
Дәлелде:. АС диагоналын жүргіземіз. сонда  АВС және
АВС және  АДС шығады.
АДС шығады.
 ВАС+
ВАС+  В+
В+  ВСА=180º (1)
ВСА=180º (1)
 САД+
САД+  Д+
Д+  АСД=180º (2)
АСД=180º (2)
(1) мен (2) мүшелеп қоссақ,
 ВАС+
ВАС+  В+
В+  ВСА+
ВСА+  САД+
САД+  Д+
Д+  АСД = 360º
АСД = 360º
 ВАС+
ВАС+  САД =
САД =  ВАД
ВАД
 ВСА+
ВСА+  АСД =
АСД =  ВСД
ВСД
 ВАД+
ВАД+  В+
В+  ВСД+
ВСД+  Д = 360º
Д = 360º
Теорема дәлелденді.
Төртбұрыштың сыртқы бұрыштарының қосындысы да 360º-қа тең. Өздерің дәлелдеңдер.
IV. Есеп шығару.
Сыныпта №1 (ауызша), №2 (ауызша), №3 , №6, №7 (ауызша), №10.
№3
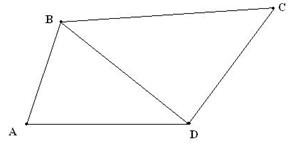 Берілгені: АВСД төртбұрыш, ВД – диогоналі
Берілгені: АВСД төртбұрыш, ВД – диогоналі
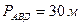 ,
, 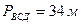 ,
, 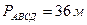
Табу керек: ВД
Шешуі: 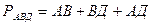 ,
,
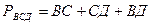 екеуін қоссақ
екеуін қоссақ
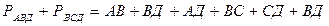
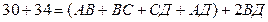
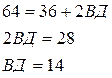
Жауабы: 14 м
№6
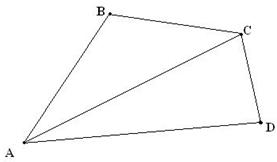
Берілгені: АВСД төртбұрыш
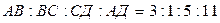
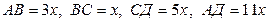
Табу керек: АВ, ВС, СД, АД
Шешуі: АС диогоналін жүргіземіз. Үшбұрыш теңсіздігі бойынша
1)  АВС-да
АВС-да 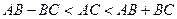
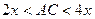 (1)
(1)
2) 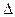 АСД-да
АСД-да 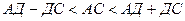
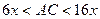 (2)
(2)
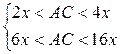
Жүйенің шешімі бос жиын, бұдан қабырғаларың қатынасы 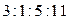 қатынасындай төртбұрыш болмайды.
қатынасындай төртбұрыш болмайды.
№10
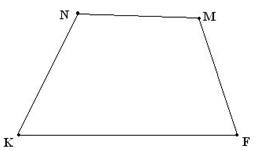
Берілгені: MNKF төртбұрыш.
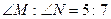
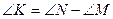 ,
, 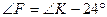
Табу керек: 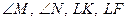
Шешуі:
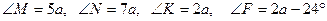
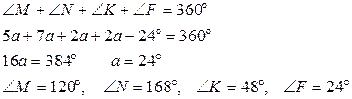
V. Сабақты қорытындылау.
VI. Үйге: №4, №5, №8
2 – сабақ
Сабақтың тақырыбы:Параллелограмм және оның қасиеттері.
Сабақтың мақсаты:
1) Білімділік:Параллелограмм анықтамасы, элементтерін,
қасиеттерін білу. Алған білімді есептер шығаруда қолдану
2) Дамытушылық:Оқушылардың логикалық ойлау қабілетін жетілдіру, тапқырлыққа, тез шешім табуға баулу
3) Тәрбиелік: Оқушыларды оқуға, жауапкершілікке, байқампаздыққа, өз ойларын сенімділікке тәрбиелеу
Сабақтың түрі: Жаңа білімді меңгерту.
Оқыту әдістері:Ауызша баяндау, сұрақ-жауап алу, есептер шығару.
Көрнекіліктер мен құрал жабдықтар:Интерактивті тақта, слайдтық презентация, сызба құралдары
Сабақтың барысы:1) Ұйымдастыру кезеңі
2) Үй тапсырмасын тексеру және өткен тақырыпты қайталау
3) Жаңа сабақты меңгерту
4) Жаңа сабақты бекіту
5) Сабақты қорытындылау, бағалау
6) Үйге тапсырма
II.Үйге берілген есептерді тексеру. Өткен сабақты бекітуге сұрақтар қойылады.
1) Қандай фигура төртбұрыш деп аталады?
2) Төртбұрыштың қандай төбелері – көршілес, қандайлары қарама-қарсы төбелер деп аталады?
3) Төртбұрыштың диогоналі деген не?
4) Төртбұрыштың қандай қабырғалары көршілес, қандай қабырғалары қарама-қарсы қабырғалар деп аталады?
5) Төртбұрыш қалай белгіленеді?
