Работа № 3. ИССЛЕДОВАНИЕ РЕЗОНАНСНЫХ ЯВЛЕНИЙ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

Цель работы – исследование условий возникновения и особенностей проявления резонанса в электрических цепях.

1. Основные положения теории

Резонансом называется режим электрической цепи, при котором собственная частота колебаний участка цепи или всей цепи в целом совпадает с частотой вынужденных колебаний. Различают два вида резонанса: резонанс напряжений и резонанс токов.

1.1 Резонанс напряжений

Резонанс напряжений возникает в цепи, когда ее эквивалентное сопротивление относительно зажимов источника приобретает чисто резистивный характер, при этом реактивные составляющие входного сопротивления взаимно компенсируется. В наиболее простом случае последовательного соединения элементов r, L, C 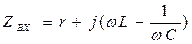, резонанс возникает при условии, когда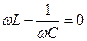 , или

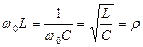
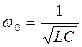
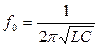
где ω₀ - резонансная частота контура; 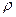- волновое сопротивление контура.

При резонансе Z_ВХ. = r , следовательно, 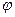= 0. Ток при резонансе 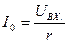, а так как X_L = X_C, то U_L0 = U_C0.

Добротность контура Q может быть определена как

Q = = =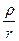

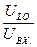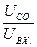
а, следовательно, Q можно определить опытным путем, измеряя U_C0.

При приближении частоты к резонансной напряжения на реактивных элементах резко возрастают. Поэтому такое явление и получило название резонанса напряжений.

Напряжения на индуктивности и емкости достигают максимума на частотах, несколько отличающихся от резонансной. Этот сдвиг зависит от добротности контура и при высокой добротности невелик. Если добротность Q>3, можно условно считать, что максимумы U_C и U_L совпадают с частотой резонанса.

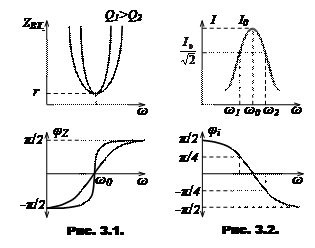
Входное сопротивление контура может быть записано в виде

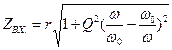
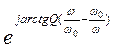
что дает возможность построить амплитудно- и фазочастотную характеристики для Z_ВХ. (рис.3.1). Характер АЧХ и ФЧХ для тока в контуре показан на рис.3.2.

Полоса пропускания – область частот, в которой 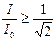. Из соотношения 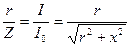следует, что на границах полосы пропускания r = ±х, 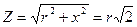. При таких соотношениях r и x 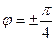. Это дает возможность определить частоты на границе полосы пропускания ( ω₁,ω₂ ) по ФЧХ рис.3.2, П = ω₂-ω₁ - абсолютное значение полосы пропускания; S = 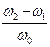- относительная полоса пропускания.

Справедливо также соотношение 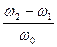= 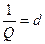, где d - затухание в контуре.

Граничные частоты могут быть определены по формуле

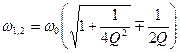
Избирательностью системы называют ее способность пропускать электрические сигналы в определенной полосе спектра сигналов при существенном подавлении сигналов вне этой полосы. Резонансный контур может выполнять функции избирательной системы.

Избирательность контура при заданной расстройке оценивается в децибелах (дБ) и может быть определена как a = 20 lg .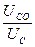

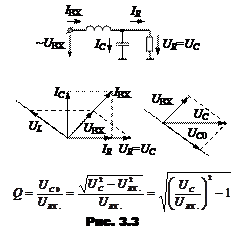Векторная диаграмма для нагруженного контура при резонансе (рис. 3.3): построение начинаем с параллельного участка - отложим горизонтально вектор тока I_R через сопротивление нагрузки, вектор напряжения U_R совпадает по направлению со своим током и равен напряжению U_C на параллельно включенной емкости, ток через емкость I_C опережает свое напряжение на угол p/2, сумма токов I_C и I_R равна входному току I_ВХ., напряжение на индуктивности опережает свой ток, т.е. I_ВХ., на угол p/2. Проводим прямую линию под прямым углом к вектору I_ВХ., параллельно этой линии проводим пунктир от конца вектора U_R до пересечения с вектором I_ВХ. , от точки пересечения проводим пунктир параллельно U_R до пересечения с прямой линией– получаем параллелограмм, откладываем на диагонали параллелограмма вектор U_ВХ., который при резонансе совпадает по направлению с I_ВХ., и вектор U_L на стороне параллелограмма, т.е. «подгоняем» величины U_ВХ. и U_L.

Для данной схемы напряжение U_C≠U_C0, поэтому напряжение U_C0 находим построением: на перпендикуляре к вектору U_ВХ. находим проекцию U_C . Величину U_C0 находим по Пифагору из прямоугольного треугольника. Если величина U_C значительно превышает U_ВХ. (более чем в три раза), то единицей под корнем можно пренебречь.

1. Предварительная подготовка

Студенты, пропустившие лаб. работы №1 и №2 и не знающие номер своего стенда, выполняют предварительный расчет для произвольно взятого стенда.

Студенты, записавшиеся на отработку, выполняют предварительный расчет для

произвольно взятого стенда.

Таблица 3.1.

2.1. Для схемы, изображенной на рис.3.4, рассчитать для R_М = 160 и R_М = 640 Ом : резонансную частоту f₀, добротности Q, граничные частоты полосы пропускания f₁ и f₂ , действ. зн. силы тока при резонансе I₀, действ. значения напряжениий на емкости при резонансе U_С0 и на границах полосы пропускания U_С(f₁) и U_С(f₂), R_Ш=100 Ом, активное сопротивление катушки индуктивности R_LA = 20Ом,напряжение на генераторе U_Г = 2 В.

	ст. № 1	ст. № 2	ст. № 3	ст. № 4	ст. № 5	ст. № 6	ст. № 7	ст. № 8	ст. № 9	ст. № 10
LA , мГн	43,8	45,1	44,9	45,5	46,7	48,1	45,9	45,3	46,3	46,5
CA , мкФ	0,02269	0,02110	0,02338	0,02255	0,02252	0,02155	0,02243	0,02303	0,02393	0,02357

2.2. Рассчитать добротности и резонансные частотынагруженного контура (рис 3.5) при R_M = 2560 Ом и R_M = 5120 Ом. Записать выражение для Z _ВХ. (с учетом параллельного соединения C_Aи R_M), выделить мнимую часть и приравнять ее нулю, вычислить ω₀, действительная часть этого выражения равна эквивалентному активному сопротивлению цепи R_ЭКВ.. Вычислить значения Q = ω₀L_A / R_ЭКВ.. Сделать вывод о влиянии нагрузки на резонансную частоту и добротность. Чему равны добротность и резонансная частота при R_M→ ∞?

Задание на выполнение эксперимента

3.1. Включить «СЕТЬ», «ГЕНЕРАТОР», «V2», «V3-φ». Осциллограф не включать. Установить форму напряжения на выходе генератора – на плате Г2 переключателем выбрать синусоиду f var~.

Собрать схему (рис. 3.4, восемь проводников), соединить правое верхнее гнездо «ВЫХОД» на плате Г3 генератора с левым верхним гнездом «ОПОРН.» фазометра, R_Ш = 100 Ом.

Установить U_Г = 2 В, R_M = 640 Ом.

Магазин сопротивлений R_M переключать плавно, с остановками, т.к. при быстром переключении возможна поломка переключателя.

Плавно изменяя частоту, записать показания вольтметра и фазометра, а также значения частот для показаний фазометра 45^о, 0^о, -45^о. При снятии показаний фазометра сложно отметить при какой частоте он показывает ноль. В таком случае можно отметить f₀ при одновременном свечении индикаторов «L» и «C», полученное значение f₀ сразу записать в таблицы 3.2 и 3.3.

Установить R_M =160 Ом и повторить измерения. При резонансе установить и записать максимальное значение U_RШ , а значение f₀ записать из табл. 3.2, т.к. изменение f₀ не превышает погрешность измерения частотомера.

На частоте 2 кГц φ_i не измерять, записать только U_RШ , т.к. практически отсутствует сигнал на измерительном канале фазометра - в этом можно убедиться, отключив провод от входа «ИЗМ.j » (опыт «холостого хода»): при увеличении частоты от 2 кГц стрелка фазометра совершает такие же колебания, как и при подключенном проводе. При подключенном проводе на частоте ~ 3 кГц происходит «захват» сигнала. Можно измерить φ_i косвенно: переключить схему так, как описано в п. 3.2., подключить канал «ИЗМ.j » к емкости, измерить φ_UC и вычислить φ_i = 90 - φ_UC (в соответствии с векторной диаграммой напряжений для данного контура), но это только усложняет эксперимент. Таким же способом можно установить резонанс при φ_UC= 90^о.

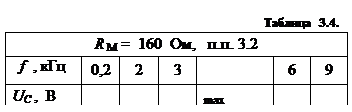
3.2 На генераторе поменять местами провода «ВЫХОД» и «┴» (провод, соединяющий «ВЫХОД» генератора с «ОПОРН.» фазометра оставить на месте) и переключить вольтметр в точку "A" схемы (рис. 3.4). Исследовать U_С ( f ), R_М = 160 Ом (табл. 3.4).

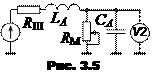3.3. Собрать схему (рис. 3.5, провод, соединяющий «ВЫХОД» генератора с «ОПОРН.» фазометра оставить на месте). Установить R_M = 2560 Oм.

Исследовать U_C ( f ) (табл. 3.5). Повторить опыт при R_M = 5120 Ом.

Схему не разбирать.

3.4. Установить R_М=640 Ом, частоту f = 2 кГц. Выключить «V2», «V3-φ», «ГЕНЕРАТОР», «СЕТЬ».

4. Обработка и анализ результатов измерений

4.1. Построить φ_i(f)– две зависимости на одном графике (R _M=640 Ом и R _M=160 Ом), для

каждой зависимости вертикальными отрезками показать границы полосы пропускания ивычислить значения Q .

4.2. Построить I _ВХ.(f) – две зависимости на одном графике (R _M=640 Ом и R _M=160 Ом),

для каждой зависимости провести линию на уровне 0,707I ₀ , вертикальными отрезками показать границы полосы пропускания (не переносить их с графика φ_i) .

4.3. Построить Z _ВХ.(f) – две зависимости на одном графике (R _M=640 Ом и R _M=160 Ом),

для каждой зависимости провести линию на уровне 1,41 Z_MIN , вертикальными отрезками показать границы полосы пропускания. Для Z _ВХ.(f) брать значения из таблиц не более 2 кОм или изменить масштаб по оси ординат. Значениям 2 кОм соответствуют значениям силы тока 1 мА на графиках I _ВХ.(f), т.е. для каждой зависимости I _ВХ.(f) можно определить соответствующие этому значению частоты и затем перенести их на график Z _ВХ.

4.4. Построить U_С(f) (п.п. 3.2), отметить частоту резонанса f₀ (известна из первого опыта, табл. 3.2), графически определить напряжение на емкости при резонансе U_C0, которое может не совпадать с максимальным. Вычислить Q (только для R_М=160 Ом).

4.5. Построить две зависимости U_С(f) для нагруженного контура (п. 3.3) – всего три

зависимости на одном графике, сделать выводы о влиянии нагрузки на добротность. Для R_M = 2560 Oм и R_M = 5120 Ом значения Q не вычислять.

4.6. Все зависимости подписать, на каждой указать значения R_M.

4.7. Сравнить результаты эксперимента с расчетными данными.

5. Вопросы для самопроверки и защиты

5.1. Как рассчитать избирательность в последовательном контуре?

5.2. В каком случае напряжения на отдельных элементах схемы могут быть больше напряжения генератора?

5.3. Что такое полоса пропускания ?

5.4. Как можно определить граничные частоты ?

5.5. Чему равно реактивное сопротивление контура на границах полосы пропускания, если известно его эквивалентное активное сопротивление ?

5.6. От чего зависит диапазон частот, при котором U_С >U_ВХ.?

5.7. Построить векторные диаграммы при f<f₀; f=f₀; f>f₀ для схемы на рис.3.5.

5.8. Симметрична ли кривая зависимости I(f) и U_С(f) при малых и больших добротностях ?

5.9. Нарисуйте схемы с использованием избирательных свойств контура, чтобы на выходе ослаблялась определенная полоса частот.

5.10. Объяснить влияние величины R_Ш и R_М на добротность (рис.3.4).

5.11. Как следует изменить параметры колебательного контура, чтобы изменить f₀ , не меняя полосы пропускания ?

Как изменятся свойства резонансного контура (рис. 3.4), если дополнительно

последовательно включить в него индуктивность L_A и емкость C_A ? Как изменятся при это изменятся зависимости φ_i(f), I _ВХ.(f), Z _ВХ.(f)?

При подготовке к лабораторной работе рекомендуется ознакомиться с материалами [7, с.167-211].