Методы борьбы с тупиками
В настоящее время выделяются следующие основные подходы к проблеме борьбы с тупиками [,] :
n предотвращение;
n недопущение;
n обнаружение и последующее восстановление *).
Перечисленные подходы являются универсальными и применяются как в системах с общей так и с раздельной памятью []. В каждом из типов систем имеются свои особенности реализации данных методов.
5.4.1 Предотвращение тупиков
Методы предотвращения тупиков (или как иногда говорят, самозамыкания) связаны с устранением одного или нескольких условий для их возникновения. Данный подход получил название стратегии Ханвендера, который в своей работе [] показал, что возникновение тупика не возможно, если нарушено хотя бы одно из четырех необходимых условий.
Существует три основных способа предотвращения тупиков согласно этой стратегии [,,].
При первом способе, называемом опережающим требованием, все потенциально необходимые ресурсы запрашиваются одновременно. До запроса процесс не должен удерживать какие-либо ресурсы. Система предоставляет процессу запрашиваемые ресурсы или переводит его в состояние ожидания. Тем самым устраняется условие ожидания дополнительных ресурсов.
Этот способ имеет очевидные недостатки: во-первых, он приводит к неэффективному использованию ресурсов, так как ресурсы могут удерживаться процессом задолго до их реального использования или вообще могут не потребоваться процессу в текущей реализации, во-вторых, этот путь приводит к бесконечному откладыванию.
Процесс может быть разделен на несколько задач, которые выполняются относительно независимо друг от друга. В этом случае ресурсы выделяются для каждой задачи в отдельности. Это позволяет несколько сократить «простой» ресурсов, но требует более интенсивной работы менеджера ресурсов. Кроме того процесс может периодически требовать ресурсы, использовать их и возвращать затем все занятые ресурсы системе.
Второй способ реализуется путем упорядочения ресурсов и иногда называется иерархическим распределением [md]. Ресурсы делятся на классы, каждому из которых присваивается номер. Процессы могут запрашивать ресурсы только строго с большими номерами, чем те которые они удерживают. Этот способ устраняет четвертое условие, а именно круговое ожидание. На рис. 5.2 показана именно такая ситуация. Если поместить две единицы ресурса в разные классы 1 и 2, то процесс p1, получивший ресурс с номером 1 может запросить только ресурс с номером 2, в то время как второй процесс p2 переводится в состояние ожидания 1-го ресурса. После того как первый процесс освободит первый ресурс, его получит второй процесс и запросит ресурс с номером 2 и, если он еще занят, перейдет в состояние ожидания 2-го ресурса, до его освобождения первым процессом.
Назначаемые номера ресурсов должны отражать наиболее вероятный порядок использования ресурсов. Обычно дефицитным ресурсам присваиваются большие номера.
Данный подход так же является недостаточно гибким. Вследствие невозможности получения ресурса с маленьким номером без предварительного возвращения системе ресурсов с большими номерами процессы должны запрашивать ресурсы с маленькими номерами задолго до фактической потребности в них. Некоторые процессы блокируются в очереди за процессами, которые реально еще долго им не понадобятся, но они вынуждены их запрашивать, чтобы соблюсти искусственно установленный для них порядок запросов на ресурсы.
Третий способ устраняет условие неперераспределяемости ресурсов. Если процесс в результате сделанного запроса не может получить нужный ему для продолжения выполнения ресурс, то он останавливается и все или часть занятых им ресурсов отбирается. При этом процесс теряет всю или часть сделанной им работы. Способ является простым, но может привести к бесконечному откладыванию (indefinite postponement) , выражающемуся в том, что процесс может многократно запрашивать и возвращать один и тот же ресурс [дтл]. Если выполнение такого процесса не отложить, переведя его в состояние блокировки, то это приведет к непроизводительному растрачиванию вычислительных ресурсов и резкому падению производительности системы. Откладывание или блокировка подобных процессов может оказаться слишком длительной. Процесс «зависнет» в системе.
5.4.2 Недопущение или обход тупиков
Алгоритмы недопущения или обхода тупиков можно назвать алгоритмами опережающего требования. Тупики возможны и задача состоит в таком распределении, которое не приведет к тупиком ситуациям. Требования процессов на ресурсы анализируются по специальным алгоритмам и, если ситуация безопасна относительно тупика, ресурсы выделяются.
Наиболее известным алгоритмом подобного типа является, так называемый, алгоритм банкира, предложенный Дейкстра []. Алгоритм выполняет действия аналогичные действиям банкира, имеющего некоторый капитал наличных денег. Эти деньги банкир хочет ссудить в долг на некоторый срок. Заемщики часто вынуждены брать дополнительную ссуду, чтобы вернуть хоть что-то. Заимодавец должен быть достаточно осмотрительным и так распределять кредиты, чтобы заемщики смогли вернуть ему деньги, и в то же время достаточно гибким, чтобы дать как можно больше кредитов.
В качестве банкира выступает менеджер ресурсов. Заемщики - процессы делают заявки на ресурсы. Заявки отражают максимальную потребность процессов в ресурсах данного класса. Процесс не может затребовать ресурсов больше, чем указано в заявке. Это позволяет менеджеру ресурсов проводить предварительный анализ возникающей ситуации и не допускать возникновение тупика.
Текущее распределение ресурсов может быть описано следующим образом:
type
n=Number_of_Process;
Process_Resource_State =
record
Claim:integer; {заявка}
Held:integer; {удерживаемые ресурсы}
Request:boolean;{флаг блокировки процесса}
end;
Allocation_State =
record
Hold:array [1..n] of Process_Resource_State;
Free:integer;{не распределенные ресурсы}
end;
Число процессов фиксировано. Число ресурсов фиксировано. Для осуществления распределения необходимо выполнение следующих условий:
1) процесс не может требовать больше ресурсов, чем имеется в системе;
2) процесс не может получить ресурсов больше, чем указано в требовании (заявке);
3) сумма всех полей Held, отражающая количество распределенных ресурсов данного класса, не может превышать суммарного количества единиц ресурса в системе.
Менеджер ресурсов гарантирует, что тупиковая ситуация не наступит. Каждое требование проверяется по отношению к количеству ресурсов в системе, а каждый запрос проверяется относительно суммы всех заявок на ресурс. Менеджер ресурсов ищет последовательность процессов, которая может завершиться. Если такая последовательность есть, то система не находится в тупике.
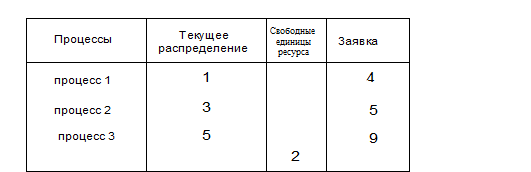
Рассмотрим пример. На рис.5.4 а) показано текущее распределение единиц ресурса одного
типа.
а)
б)
Рис. 5.4.
Показанное на рис.5.4.а) состояние распределения является надежным или безопасным относительно тупика, так как здесь имеется последовательность процессов 2, 1, 3, которая может завершиться. Действительно, процесс 2 не может запросить больше двух единиц ресурса. Система имеет две свободные единицы и процесс 2 может завершиться. Завершившись процесс 2 вернет системе 5 единиц, которые затем могут быть выделены процессу 1 ( максимальная потребность которого - 4 ). Завершившись первый процесс освободит 4 единицы. Потребность третьего процесса в дополнительных единицах ресурса не превышает четырех единиц и он также может завершиться.
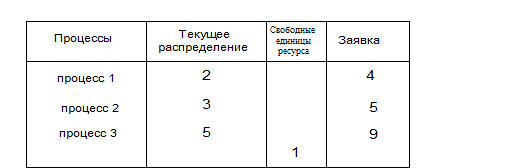
Однако, если текущее состояние надежно, это не значит, что все последующие состояния будут надежными. Например, если система из состояния, показанного на рис.5.4.а) перейдет в результате удовлетворения запроса первого процесса на одну единицу ресурса в состояние, показанное на рис.5.4.б), то она перейдет из надежного в ненадежное состояние. В новом состоянии нельзя гарантировать успешного завершения всех процессов. В этом состоянии отсутствует последовательность процессов, которые могут гарантированно завершиться.
Ненадежное состояние не обязательно приведет к тупику. Процессы могут не запроситть максимально заявленного количества единиц ресурса.
Итак, формально состояние является безопасным, если существует последовательность процессов такая что:
1) первый процесс в последовательности обязательно завершится, так как даже, если он запросит максимально заявленное количество единиц ресурса у системы имеется необходимое количество единиц для удовлетворения запроса;
2) второй процесс может завершиться, если первый завершится и вернет системе все занятые им единицы ресурса, что в сумме со свободными единицами позволит удовлетворить максимальную потребность второго процесса;
3) i-ый процесс в последовательности может завершиться, если все предыдущие процессы успешно завершатся и сумма освобожденных и свободных ресурсов сможет удовлетворить максимальную потребность процесса в данном ресурсе.
Таким образом, всякий раз, когда процесс делает новый запрос, менеджер ресурсов должен найти успешно завершающуюся последовательность процессов и только в этом случае запрос может быть удовлетворен. Необходимо исследовать n! последовательностей прежде, чем признать состояние безопасным. Затраты могут быть снижены пропорционально n², если отказаться от необходимости выделять запрашиваемые ресурсы согласно порядку следования в безопасной последовательности распределения.
Алгоритм называется O(n²), где O означает «order of», и работает следующим образом:
S = количество процессов;
цикл пока S <> []
начало
найти процесс А в последовательности S, который может завершиться;
если нет, то состояние небезопасное - вывести процесс А из S, отобрать
у А ресурсы и добавить их пул
нераспределенных ресурсов;
конец;
состояние безопасное;
В этом случае ресурсы распределяются в порядке следования запросов до тех пор, пока имеется некоторая безопасная последовательность после каждого удовлетворенного запроса.
Еще менее затратный алгоритм был предложен Хаберманом []. Менеджер ресурсов поддерживает массив S[0..r-1], где r - число единиц ресурса.
S[i] = r - i для всех i : 0 £ i < r;
если процесс, заявивший C единиц ресурса и удерживающий h единиц ресурса запрашивает еще одну единицу, то S[i] декрементируется для всех i : 0 ≤ i < C-h.
Если какое-то из S[i] становится отрицательным, то состояние - опасное.
Итак, все условия возникновения тупиков выполняются. Процессы монопольно используются разделяемые ресурсы. Процессам разрешено удерживать ресурсы и динамически запрашивать дополнительные ресурсы. В классическом варианте алгоритма у процесса не отбираются уже выделенные ему ресурсы. Если запрос отклоняется, процесс переводится в состояние ожидания до благоприятного момента. Система удовлетворяет только те запросы, при которых ее состояние остается безопасным. В силу того, что система всегда имеет возможность реализовать некоторое состояние, все запросы могут быть удовлетворены в течение конечного периода времени и все процессы смогут завершить свою работу.
5.4.3 Недостатки алгоритма банкира.
Алгоритм банкира имеет скорее теоретический, чем практический интерес. Плата за такой подход очевидна: алгоритм буквально пожирает процессорное время и память. Кроме того, такие предположения, как фиксированное число ресурсов и фиксированное число процессов, необходимость указывать в заявке максимальную потребность в запрашиваемых ресурсах, что требует знания априорной информации о потребностях, в современных системах неприемлемы. Предположения, что ресурсы будут выделены и процесс со временем все-таки вернет ресурсы, в реальных системах должны быть более определенными, ограниченными во времени.
5.4.4. Обнаружение тупиков.
Тупики допускаются. Все требования процессов на ресурсы удовлетворяются сразу. Имеются все условия возникновения тупиков. Задача системы обнаружить тупик и затем предпринять некоторые действия по выходу из тупика. Таким образом, выход из тупика является второй частью задачи обнаружения, хотя и имеет самостоятельное теоретическое о практическое значение.
Наиболее полно проблема распознавания тупиков освещена в работе [].
Если систему рассматривать как декартово произведение множества состояний, где под состоянием понимается состояние ресурсов - свободны они или распределены, причем состояние может изменяться процессами в результате запроса и последующего приобретения ресурса и освобождения ресурса, то система находится в тупике, если она не может поменять своего состояния. Или, другими словами, процесс находится в тупике в некотором состоянии, если он не может изменить это состояние ни запросом и последующим приобретением ресурса, ни освобождением ресурса.
Вопрос каким образом можно определить находится ли какое-то количество взаимодействующих друг с другом процессов в тупике решается с использованием графовой модели Холта.
Граф L = ( X,U;P ) задан, если даны множество X ¹ (вершин), множество U (ребер) и инцидентор - трехместный предикат P, причем P( x,u,y ) означает высказывание: «ребро u соединяет вершину x с вершиной y» и удовлетворяет двум условиям:
а) P определен на всех таких упорядоченных тройках элементов x, u, y, для которых x, y Î X и
u Î U ;
б) " uÎU $ x, y ÎX { P( x,u,y ) & " x',y'Î X [ P( x',u',y' ) Þ ( x = x' & y = y') V ( x = y'&
y = y'& y = x')]}, т.е. каждое ребро соединяет какую-то пару (упорядоченную) вершин x, y, но кроме нее может соединять еще только обратную пару y ,x (определение дано по А.А.Зыкову) [эн].
Ребро, соединяющее x с y, но не y с x называется дугой.
Модель Холта представляет собой двудольный или бихроматический граф, в котором множество вершин X разбивается на два подмножества,множество вершин-процессов = p1,p2,..., pn и множество вершин-ресурсов r1,r2,..., rm: X = вершины соединяются дугами, причем никакая дуга не соединяет вершин одного и того же подмножества.
Дуга ( r,p ), направленная из вершины r Îк вершинеpÎназывается приобретением. Дуга ( p,r ), направленная из вершины pÎк вершине r Îназывается запросом.
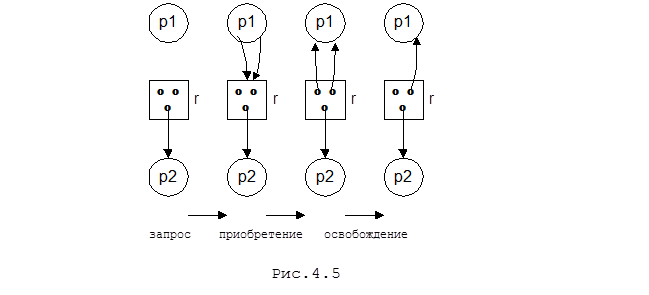
На рис.4.5 показаны операции запроса и приобретения и освобождения единицы ресурса. Не заблокированный в тупике процесс приобретает любые ресурсы, которые ему нужны для выполнения, а затем освобождает уже не нужные ему ресурсы. Освободившиеся ресурсы могут быть распределены другому процессу, ожидающему их.
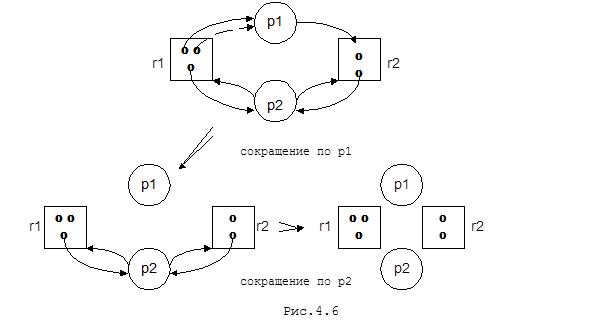
Обнаружить процессы, попавшие в тупик, можно методом редукции (сокращения) графа. Граф сокращается процессом pi, который не является ни заблокированной, ни изолированной вершиной, с помощью удаления всех ребер, входящих в pi и выходящих из pi. Процедура сокращения соответствует действиям процесса по приобретению запрошенного ранее ресурса и последующему освобождению всех его ресурсов. В этом случае pi становится в графе изолированной вершиной. На рис. 4.6 показан полностью сокращаемый граф и последовательность его сокращений.
В самом деле, рассмотрим процесс p1 Этому процессу выделены две единицы ресурса r1 и он запросил одну единицу ресурса r2. Эта единица свободна, следовательно граф можно редуцировать по p1. В результате будут освобождены занятые процессом единицы ресурсов и граф может быть редуцирован по p2.
Граф является полностью сокращаемым, если существует такая последовательность сокращений, которая устраняет все дуги. Если граф нельзя полностью сократить, то анализируемое состояние является тупиковым.
Если в рассматриваемом примере единица ресурса r1 была выделена процессу p1 ( рис.4.7), то граф не может быть редуцирован ни по p1 ни по p2, так как их запросы не могут быть удовлетворены. Процессы не могут продолжать выполнять свою работу и впоследствии не смогут освободить занятые ими ресурсы. Процессы находятся в тупике - процессы попали в циклическую цепочку запросов.
Таким образом, тупик может быть только результатом запроса. А необходимым условием тупика является цикл в графе. Некоторое состояние есть состояние тупика, если по крайней мере два процесса находятся в тупике. Если граф нельзя сократить полностью, то все процессы, по которым нельзя выполнить сокращение находятся в тупиковой ситуации*).
В силу того, что тупик может наступить только в результате запроса, редукцию надо применять только после запроса некоторого процесса pi.
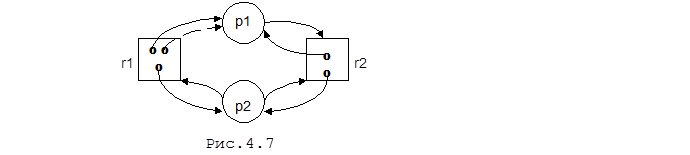 Для повторно используемых ресурсов порядок сокращения графа не имеет значения. В результате любой последовательности сокращений будет получен один и тот же несокращаемый граф[,].
Для повторно используемых ресурсов порядок сокращения графа не имеет значения. В результате любой последовательности сокращений будет получен один и тот же несокращаемый граф[,].
5.4.4.1. Представление графов и алгоритмы обнаружения.
Граф состояния системы может быть представлен или с помощью матриц, или с помощью связных списков.
В матричном виде граф может быть описан двумя матрицами, например, матрицей запросов {p,r} и матрицей распределения {r,p}, в которой каждый элемент выражает количество единиц ресурса, распределенного данному процессу. Для решения поставленной задачи необходимо иметь дополнительную информацию о количестве свободных единиц каждого из ресурсов, имеющихся в системе. Дополнительную информацию можно хранить в дополнительном столбце матрицы распределения или отдельном векторе.
При списочном представлении могут использоваться два типа связных списков. Один тип представляет распределенные любому процессу pi выделенные ресурсы и количество единиц ресурса.
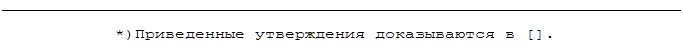
Type
process_ptr = ^Held;
Held = record
resource : resource_type; {тип ресурса}
number : integer; {число выделенных единиц}
next : process_ptr;
end;
Var p1,...,pn : process_ptr;
Для каждого процесса создается связный список выделенных ему ресурсов.
Другой тип представляет цепочку запросов процессов на ресурс rj..
Type
resource_ptr = ^Inquiry;
Inquiry = record
process : process_type;
number : integer; {количество запрашиваемых единиц ресурса}
next : resource_ptr;
end;
Var r1,r2,...,rm : resource_ptr;
Для каждого ресурса в системе составляется связанный список процессов, запросивших данный ресурс, с указанием нужного им количества единиц ресурса. Информация о количестве единиц каждого ресурса или количестве свободных единиц каждого ресурса хранится в отдельном векторе.
Списки как и таблицы должны быть монопольно используемыми ресурсами.
Для обнаружения тупика может использоваться метод прямого обнаружения, который заключается в просмотре по порядку матрицы или списка запросов. Там, где это возможно производятся сокращения до тех пор, пока нельзя будет сделать более ни одного сокращения. Процессы, оставшиеся после всех сокращений, находятся в тупике. Для самого плохого случая, когда сокращения выполняются в порядке обратном следованию процессов, число проверок равно n(n+1)/2. Причем каждая проверка требует испытания m ресурсов, таким образом время, затрачиваемое на проверки, пропорционально mn².
Более эффективный алгоритм получается, если хранится дополнительная информация о запросах: для каждого ресурса хранятся запросы, упорядоченные по размеру; для каждого процесса pi определяется счетчик ожиданий i, содержит число типов ресурсов, которые вызывают блокировку процесса в ожидании освобождения требуемого ресурса. Затем среди заблокированных процессов ищется цикл запросов.
Как уже говорилось, наличие цикла является необходимым, но не является достаточным условием тупика. Если производить распознавание тупика непрерывно, то очевидно, что тупик может наступить только после очередного запроса, который не может быть удовлетворен сразу. Таким образом, запрос является достаточным условием возникновения тупика.
В работе [] описан способ матричного представления, предложенный Бенсусан и Мерфи. Для обнаружения тупиков используются две матрицы: матрица распределения и матрица блокированных процессов. Матрицы представляются таблицами, соответственно ТРР (таблица распределенных ресурсов) и ТОП (таблица блокированных в ожидании ресурсов процессов). Для обнаружения клинча используется алгоритм, показанный на рис.4.8. Алгоритм начинает работать, когда некоторый процесс выдает запрос на какой-либо ресурс.
Для иллюстрации данного метода обнаружения тупиков рассмотрим процесс распределения единичных ресурсов. Пусть выполняется следующая последовательность действий:
1) p1 занимает r1;
2) p2 занимает r3;
3) p3 занимает r2;
4) p2 занимает r4;
5) p1 занимает r5;
6) p1 запрашивает r3; поскольку r3 занят, необходима проверка по данному алгоритму. В результате работы алгоритма получаются следующие значения: j = 1, i = 3, k = 2; таблица
ожидающих процессов (ТОП) пуста процесс с номером k = 2 не ждет никакого ресурса;
занести в таблицу ожидающих процессов (ТОП) в строку 1 номер ожидаемого ресурса 3;
7) p2 запрашивает r2;
j = 2, i = 2, k=3;
процесс с номером k = 3 не ждет никакого ресурса; занести в ТОП во 2-ю строку номер
ожидаемого ресурса 2;
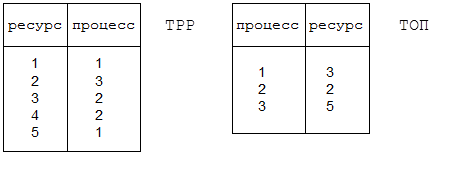
8) p3 запрашивает r5;
j = 3, i = 5,k = 1;
процесс с номером k = 1 ждет ресурс 3, следовательно l = 3; по таблице распределенных ресурсов (ТРР) находим, что 3-ий ресурс занят процессом 2 ( n = 2 );
условие ( j = n ) не выполняется выполняется присваивание k = 2; по ТОП определяем, что процесс 2 ждет ресурс 2; по таблице ТРР находим, что ресурс 2 занят процессом 3, следовательно n = 3;
условие ( j = n ) выполняется КЛИНЧ! Сохранить состояние процесса p3 для последующей попытки восстановления.
Применение этого метода избавляет от упорядочивания запросов на ресурсы по возрастанию.
Каждый запрос на занятый ресурс должен проверяться на клинч. Во время этой проверки таблицы должны использоваться монопольно.
5.4.5. Восстановление работоспособности системы.
После обнаружения тупика необходимо восстановить нормальную работу системы. Сложность вывода системы из тупика объясняется рядом причин: во-первых, возможной не очевидностью попадания системы в тупик, что особенно характерно для распределенных систем и, во-вторых, отсутствием достаточно эффективных средств для приостановления процесса на неопределенное время. Использование средств приостановки/возобновления требует значительных затрат ресурсов системы, особенно в современных системах, для которых характерно произвольное число параллельно выполняемых процессов, что приводит к невозможности прогнозирования и контроля объема соответствующих системных затрат. Некоторые процессы, такие как процессы реального времени приостанавливать вообще нельзя.
Выход из тупика в принципе возможен, если отобрать у одного или нескольких процессов некоторые из занятых ими ресурсов, приостановив выполнение процесса на некоторое время. Существует два основных подхода к решению этой проблемы: 1) последовательно отбирать ресурсы у процессов, попавших в тупик; 2) перехватывать часть нужных ресурсов у процессов, которые не находятся в тупике. При этом возникает не простая задача корректного освобождения ресурсов.
Освободить ресурс корректно можно только, если вернуть процесс к точке, предшествующей запросу на освобождаемый ресурс. Для обеспечения такой возможности необходимо предпринимать специальные меры. Известно два основных метода: 1) включение в состав ОС средств, реализующих специальную операцию «контрольная точка», для регистрации состояния процесса, предшествующего запросу на ресурс, или регистрации состояния процесса в дискретные моменты времени; 2) составление для каждой программы алгоритма возврата, который производит обратные вычисления и инвертирует состояние процесса.
Метод контрольной точки широко используется в системах реального времени. Результаты работы процесса теряются только после последней контрольной точки. Однако, во многих ОС не предусмотрены средства рестарта с контрольной точки, поэтому разработчикам прикладных систем приходится самим обеспечивать такую возможность в своих программах.
Более простым методом решения проблемы выхода из тупиковой ситуации является удаление одного или нескольких процессов. Очевидно, что вся проделанная процессами работа теряется. Процессы могут выводится из системы в соответствии в некоторой системой приоритетов, если такая имеется. Например, в качестве оценки наименьшего ущерба от удаления процесса можно взять или время выполнения процесса, или остающееся до его завершения время, если такая оценка возможна.
5.4.6.Задача «Обедающие философы»
Одной из наиболее интересных , занимательной и достаточно широко обсуждаемой в специальной литературе [,,] моделью для изучения алгоритмов распределения ресурсов и связанных с ними проблем является задача об обедающих философах, предложенная Дейктра.
За круглым столом сидят пять философов, которые едят спагетти (или рис) из тарелок, стоящих перед ними. На столе лежит ровно пять вилок (или палочек), по одной между каждой тарелкой. Философы для соблюдения правил хорошего тона должны есть спагетти двумя вилками одновременно, причем они не могут тянуться за вилкой через весь стол, а должны использовать вилки, лежащие рядом с тарелкой (рис.4.7.). Действия каждого философа очень просты: философ думает некоторое время, затем ест некоторое время. Очевидно, что два философа не могут одновременно есть одной и той же вилкой, т.е. в задаче имеется условие взаимоисключения, предполагающее монопольное использование ресурсов.
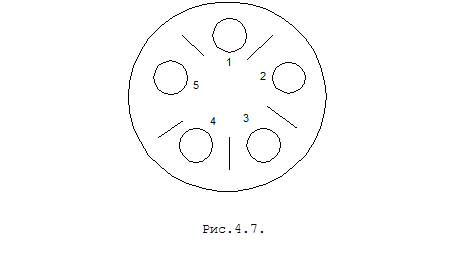
Рассмотрим следующие алгоритмы:
1) вилки выделяются по одной, то ест философ берет сначала правую, а затем левую вилки, ест некоторое время, кладет правую, а затем левую вилки;
2) философ берет обе вилки одновременно, ест некоторое время, кладет обе вилки одновременно;
3) вилки выделяются по одной - философ берет сначала правую, а затем, если левая вилка отсутствует, кладет правую вилку и продолжает свои попытки завладеть обоими вилками до тех пор пока не получит их, ест некоторое время, после чего кладет правую вилку, затем кладет левую вилку.
Проанализируем последствия, к которым могут привести перечисленные последовательности действий.
Первый алгоритм грозит всем философам голодной смертью. Если все философы одновременно возьмут правую вилку, то в левую руку взять будет нечего. Типичная тупиковая ситуация.
Второй алгоритм грозит голодной смертью только некоторым из мыслителей. Например, первому и третьему философу удалось завладеть обеими вилками. Они поели и положили обе вилки, но сразу же взяли их снова. Или другой вариант: третий положил вилки, а четвертый взял их, затем он их положил, но их взял снова третий; в это время первый положил вилки и их взял пятый и т.д. Второй философ останется голодным, так как он не может получить в свое пользование обе вилки одновременно. Этот философ постоянно блокирован в ожидании необходимых ресурсов. Такая ситуация называется «зависание» (starvation).
Третий алгоритм так же опасен, но возможностью бесконечного откладывания. Например, первый взял правую, а затем и левую вилку. Тоже сделал третий. Затем первый положил правую и через некоторое время левую вилки. Но третий продолжает есть. Второй ждет правую вилку. Первый снова берет правую вилку и свободную левую. Третий положил правую и ее взял второй, но он не может взять левую вилку и вынужден освободить правую вилку и т. д. Второй многократно запрашивает и освобождает один и тот же ресурс. Такая ситуация называется бесконечным откладыванием.
Первый алгоритм никак не ограничивает действия философов. И как видно все они становятся жертвой тупика.
Второй алгоритм предполагает одновременное получение всех необходимых ресурсов. Тупик отсутствует, так как нет условия кругового ожидания. Однако, существует возможность «зависания».
Третий алгоритм предусматривает освобождение ресурсов, если нет возможности получить все необходимые для продолжения ресурсы. Условие возникновения тупика не соблюдено. Но снова некоторых философов поджидает голодная смерть в результате бесконечного откладывания.
Вопросы для самопроверки.
5.1. Системы со спулингом допускают, чтобы распечатка данных началась еще до окончания процесса. Пусть процесс сформировал 1000 строк, которые были приняты механизмами спулинга и помещены в буфер на диске. Допустим, что этот процесс до своего завершения сформирует еще 19000 строк для печати. После формирования первых 1000 строк принтер освободился и началась их распечатка. Что произойдет после завершения распечатки этой тысячи сток в каждом из следующих случаев:
1) процесс закончит формирование 19000 строк для печати;
2) процесс еще продолжает выполняться.
При выборе решения следует учитывать, что листинг не должен иметь пропусков.
5.2. Первые системы со спулингом работали с буферами фиксированного объема. В современных системах предусмотрена возможность динамического изменения размера буфера в процессе работы. Каким образом это помогает уменьшить вероятность тупиковых ситуаций? Однако, тупики полностью не исключаются. Как такая система может попасть в тупик?
5.3. Что такое бесконечное откладывание и «зависание»? Что у них общего между собой и общего с тупиком? В чем различия?
5.4. Объясните почему средства обхода тупиков интуитивно кажутся более привлекательными по сравнению со средствами предотвращения тупиков.
5.5. Алгоритм банкира, предложенный Дейкстра, имеет ряд недостатков, которые препятствуют его использованию в реальных системах. Поясните, почему каждое из указанных ниже ограничений может рассматриваться как недостаток алгоритма:
а) количество распределяемых ресурсов считается постоянным;
б) число процессов считается постоянным;
в) ОС гарантирует, что запросы на ресурсы будут удовлетворены за конечный период времени;
г) процессы должны возвратить системе занятые ими ресурсы в течение конечного интервала времени;
д) для работы алгоритма необходимо иметь информацию о максимальной потребности процессов в ресурсах.
5.6. Предположим, что в системе реализовано распределение ресурсов по иерархическому принципу. Пусть процесс удерживает ресурс из третьего класса и для продолжения ему потребовался ресурс из второго класса. Найдите выход из возникшей ситуации, если он существует.
5.7. Допустим, что имеется два класса ресурсов. Для следующего текущего распределения определите какие, если такие имеются, процессы находятся в тупике:
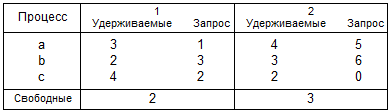
5.7. Допустим, что имеется два класса ресурсов. Для следующего текущего распределения определите какие, если такие имеются, процессы находятся в тупике:
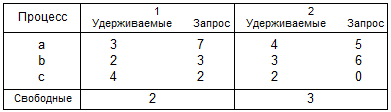
5.8. Предложите ненадежное распределение, в котором три процесса и один класс ресурсов, содержащий четыре единицы, причем каждый процесс может запросить две единицы ресурса.
5.9. Какое из следующих событий может перевести систему из надежного в ненадежное состояние? Какое может привести из не тупикового в тупиковое состояние?
А) процесс делает запрос в рамках заявки.
Б) процесс делает запрос сверх заявленного.
В) запрос в рамках заявки удовлетворен.
Г) процесс заблокирован в очереди ожидающих освобождения ресурса процессов.
Д) процесс увеличил свою заявку.
Е) процесс освобождает ранее полученные ресурсы.
Ж) вновь созданный процесс указывает свои потребности.
5.10. В предположении, что три первых условия возникновения тупика выполняются, проанализируйте следующую стратегию: процессам присваиваются уникальные значения приоритетов; когда имеется более чем один процесс, ожидающих освобождения некоторого ресурса, и этот ресурс освобождается, он выделяется процессу с наивысшим приоритетом.
5.11. Иногда информации о максимальных потребностях процессов в ресурсах достаточно для обхода тупиков без значительных накладных расходов. Рассмотрим следующую ситуацию, предложенную Холтом. Пусть m процессов используют n идентичных ресурсов. Ресурсы могут захватываться и освобождаться строго по одному. Ни одному из процессов никогда не требуется более n ресурсов. Сумма максимальных потребностей всех ресурсов m+n. Покажите, что в такой ситуации тупики невозможны.
