Логические отношения между формулами КЛВ, их характеристика.

Иногда в процессе рассуждения бывает важно установить, в каких логических отношениях находятся те или иные высказывания. Допустим, при расследовании ограбления банка были получены показания трех свидетелей. Один говорит: «Если виновен Браун, то виновен и Джонс», другой: «Если виновен Джонс, то виновен и Браун», а третий – «Виновен только один из них: либо Браун, либо Джонс». Могут ли они все трое лгать? Могут ли они все трое говорить правду? Для решения этой задачи достаточно построить совместную

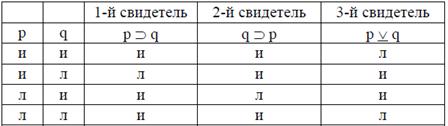
таблицу для показаний трех свидетелей. Пусть р означает, что виновен Браун, а q – что виновен Джонс.

Из данной таблицы видно, что свидетели не могут все втроем говорить правду, но не могут и все втроем лгать. Более того, оказывается, что даже двое свидетелей не могут вместе лгать – в каждой строке только одна формула является ложной, а две – истинными. В качестве фундаментальных логических отношений в КЛВ

выделяют отношения совместимости по истинности, совместимости по ложности и логического следования.

Формулы А и В совместимы по истинности, если и только если в их совместной таблице истинности существует хотя бы одна строка, где они вместе принимают значение «и».

Формулы А и В совместимы по ложности, если и только если в их совместной таблице истинности существует хотя бы одна строка, где они вместе принимают значение «л».

Из формулы А логически следует формула В, если и только если во всех строках, где А принимает значение «и», В тоже принимает значение «и».

На основе этих отношений могут быть определены другие типы отношений между формулами. Наиболее употребимые из них:

(1) Отношение противоречия (контрадикторности). Формулы А и В находятся в отношении противоречия, если и только если они несовместимы по истинности и несовместимы по ложности.

(2) Отношение противоположности (контрарности). Формулы А и В находятся в отношении контрарности, если и только если они совместимы по ложности и не совместимы по истинности.

(3) Отношение подпротивоположности (субконтрарности).

Формулы А и В находятся в отношении субконтрарности, если и только если они совместимы по истинности и не совместимы по ложности.

(4) Отношение логической эквивалентности. Формулы А и В находятся в отношении логической эквивалентности, если и только если из формулы А логически следует формула В, а из формулы В логически

следует формула А.

(5) Отношение логической независимости. Формулы А и В находятся в отношении логической независимости, если и только если они совместимы по истинности, совместимы по ложности и не следуют

логически друг из друга.

(6) Отношение логического подчинения. Формула В логически подчиняется формуле А, если и только если из формулы А логически следует формула В, но не наоборот.

24.Основные способы правильных умозаключений КЛВ, их характеристика.

Основные способы правильных умозаключений КЛВ, их характеристика.

Условно-категорические умозаключения - это двухпосылочные умозаключения, которые содержат импликативную посылку А É В. Другая посылка, а также заключение могут быть либо антецедентом (А), либо консеквентом (В) первой посылки, либо отрицанием того или другого (ØА или ØВ). К числу правильных условно-категорических умозаключений относятся:

А É В, А – modus ponens (утверждающий способ)

В

А É В, ØВ– modus tollens (отрицающий способ)

ØА

Таким образом, правильными являются умозаключения от утверждения антецедента (А) к утверждению консеквента (В)и от отрицания консеквента (ØВ) к отрицанию антецедента (ØА).

1) Если идет дождь, то крыши мокрые. Дождь идет. Значит,крыши мокрые.

2) Если наступает осень, с деревьев опадают листья. Листья еще не опали. Значит, осень не наступила.

Разделительно - категорические умозаключения. Эти умозаключения также являются двухпосылочными, причем в них имеется дизъюнктивная посылка (А Ú В) или строго дизъюнктивная посылка (А Ú В). Другая же посылка и заключение совпадают с одним из дизъюнктов (А или В) или с его отрицанием (ØА или ØВ).

К числу правильных разделительно-категорических умозаключений относятся:

А Ú В, ØА– modus tollendo ponens

В (отрицающе-утверждающий способ)

А Ú В, А – modus ponendo tollens

ØВ(утверждающе-отрицающий способ).

Примеры:

1) В машине кончился бензин или она сломалась. Машина не сломалась. Значит, кончился бензин.

2) В прошлую субботу подозреваемый был либо в городе, либо на даче. Он был на даче. Следовательно, в городе его не было.

Условно-разделительные (лемматические) умозаключения. Эти умозаключения содержат несколько импликативных и одну дизъюнктивную посылку. В дизъюнктивной посылке разделяются определенные варианты развития событий, каждый из которых имеет свое следствие. Рассмотрев и сравнив эти следствия, мы приходим к одному общему заключению. Если число рассматриваемых вариантов равно двум, такие умозаключения называются дилеммами:

A ÉC, B É C, A Ú B - простая конструктивная дилемма

C

A É B, A É C, ØB Ú ØC - простая деструктивная дилемма

ØA

A É C, B É D, A Ú B - сложная конструктивная дилемма

C Ú D

A É С, B É D, ØC Ú ØD - сложная деструктивная дилемма

ØA Ú ØB

В простых дилеммах заключение представляет собой простое суждение, в сложных – разделительное. В конструктивных дилеммах заключение является утвердительным, в деструктивных – отрицательным.

Если рассматривается три возможных варианта положения дел, такие умозаключения называются трилеммами, если больше – полилеммами.