Исчисление высказываний. Правила вывода.

Виды понятий по содержанию

По типу признаков понятия подразделяют на:

а)– Положительнымсчитается понятие, в котором предметы обобщаются на основании признака, которым они обладают (например, «учебник, купленный в книжном магазине»).

– Отрицательнымсчитается понятие, в котором предметы обобщаются на основании признака, которым они не обладают (например, «студент, не знающий японский язык»).

б)– Относительнымсчитается понятие, в котором предметы обобщаются на основании их отношения к другим предметам. Например, относительным является понятие о жене – «женщина, состоящая в браке с каким-то мужчиной», – поскольку его признак выделяет женщин не по их собственным качествам, а через отношение к каким-то мужчинам, то есть как одну из сторон супружеской четы.

– Безотносительнымсчитается понятие, в котором предметы обобщаются на основании их собственных свойств. Например, понятия о композиторе – «человек, сочиняющий музыку».

В заключении отметим, что осуществить полный логический анализ понятия, значит определить его универсум (род), объем и содержание, а также установить, к каким видам оно относится по всем указанным выше основаниям деления.

Обращение и превращение атрибутивных суждений.

Обращение (конверсия) – это непосредственное умозаключение, в котором субъект заключения совпадает с предикатом посылки, а предикат заключения – с субъектом посылки. Другими словами, вывод делается по схеме:

S – P

P – S

При обращении атрибутивных высказываний надо помнить следующие правила:

Качество суждения меняться не должно (из утвердительного высказывания получаем утвердительное, из отрицательного – отрицательное).

Если термин распределен в заключении, он должен быть распределен и в посылке.

Обращение общеотрицательных и частноутвердительных высказываний дает высказывания, эквивалентные исходным. Такое обращение называется чистым (conversio simplex).

S⁺eP⁺ Ни один гений не является злодеем.

P⁺eS⁺ Ни один злодей не является гением.

S^– i P ^– Некоторые студенты являются спортсменами.

P^– i S ^– Некоторые спортсмены являются студентами.

Общеутвердительные высказывания обращаются с ограничением(conversio per accidens): в заключении слово «все» заменяется на «некоторые»). Иначе нарушается правило №2.

S⁺ аP ^– Все студенты – люди.

P^– i S ^– Некоторые люди – студенты.

Частноотрицательные высказывания вообще не обращаются, так как при их обращении в принципе нельзя соблюсти сразу оба правила.

S^– o P⁺ Некоторые женщины не являются матерями.

P^– o S⁺ Некоторые матери не являются женщинами.

с) Превращение атрибутивных высказываний

Превращение (обверсия) – это непосредственное умозаключение, в котором субъект заключения совпадает с субъектом посылки, а предикат заключения является термином, противоречащим предикату посылки. Вывод делается по схеме:

S – P

S – ~P

При превращении атрибутивных высказываний нужно помнить, что:

Количество суждения меняться не должно (из общего высказывания получаем общее, из частного – частное).

Качество суждения должно измениться не противоположное (из утвердительного высказывания получаем отрицательное, из отрицательного – утвердительное).

Если оба правила соблюдены, вывод будет эквивалентен исходному высказыванию:

SаP Все космонавты являются смелыми людьми.

Sе~P Ни один космонавт не является трусом.

SeP Ни один дешевый автомобиль не является новым.

Sa~P Все дешевые автомобили являются подержанными.

SiP Некоторые умные люди являются несчастными.

So~P Некоторые умные люди не являются счастливыми.

SoP Некоторые студенты не опаздывают на лекции.

Si~P Некоторые студенты приходят на лекции вовремя.

Необходимо заметить, что в силлогистике каждый термин (равно как и его отрицание) должен быть непустым. Высказывания с пустыми или универсальными терминами могут привести к абсурдному заключению. Например:

Ни один образованный человек не изобрел вечный двигатель.

Следовательно, ни один изобретатель вечного двигателя не является образованным (обращение).

Следовательно, все изобретатели вечного двигателя являются необразованными (превращение).

Следовательно, некоторые необразованные люди изобрели вечный двигатель (обращение).

Здесь из истинного высказывания мы путем последовательного обращения, превращения и еще одного обращения получаем заведомо ложное заключение. Причина – наличие в посылке пустого термина «изобретатель вечного двигателя».

Язык и семантика КЛП.

С семантической точки зрения выражения языка можно подразделить на категории в зависимости от того, какой тип значения им соответствует. Впервые теорию семантических категорий создал польский логик К. Айдукевич.

Базисными семантическими категориями являются имя (n) и предложение (s). Под именем имеется в виду выражение, обозначающее какой-либо предмет или множество предметов; под предложением – выражение, обозначающее истину или ложь. Все остальные семантические категории представляют собой функции, преобразующие некоторое количество выражений одной базисной категории в выражение другой (либо той же самой) базисной категории. Например, союз «и» соединяет два предложения в одно, более сложное. Значит, он имеет сематическую категорию ss/s (преобразует два разных выражения типа s в одно выражение типа s).

Как замечал К. Айдукевич, все богатство семантических категорий естественного языка чрезвычайно трудно описать. Наиболее хорошо изученными в логике являются следующие категории:

Семантическая категория	Сим-вол	Тип значения	Пример
Предложение (пропозиция)	s	Истинностные значения (истина или ложь)	«Лондон–столица Англии» «Лондон – большой город»
имя	n	предметы	«Лондон», «город», «Англия» (в выражениях типа «Лондон – большой город» и «Лондон – столица Англии»)
функтор	n/n, nn/n	предметно-предметные функции	«столица» (в выражениях типа «Столица Англии – большой город»)
предикатор	n/s, nn/s	предметно-истинностные функции	«большой» (в выражениях типа «Этот город – большой»)
пропозициональная связка	s/s, ss/s	истинностно-истинностные функции	«и», «или», «если то», «не», «хотя»

Семантические принципы

Принцип однозначности: каждое имя должно иметь только одно значение (экстенсионал). С нарушением этого принципа связана ошибка, которую называют «подмена значения».

Существование Плутона было доказано астрономами.

Плутон – это бог.

Существование бога было доказано астрономами.

Здесь слово «Плутон» используется в двух значениях: в первой посылке имеется в виду планета Солнечной системы, во второй – божество из древнегреческой мифологии. Когда значения слова различаются столь явно, подмену заметить легко. Но если они хотя бы частично совпадают друг с другом, например одно является обычным, а другое – расширительным (или, наоборот, специализированным), ошибка может остаться незамеченной. Иногда подмена значения производится в несколько шагов, каждый из которых сам по себе не вызывает подозрения.

Принцип предметности: предложение должно говорить о предметах, обозначаемых входящими в него именами (а не о самих этих именах). С нарушением этого принципа связана ошибка, которую называют «автонимное употребление имен».

Сравните два предложения: 1) Стул – это предмет мебели, 2) Стул – это существительное. В первом слово "стул" употребляется правильно, поскольку речь идет о предмете, а во втором – автонимно, поскольку речь идет о самом этом слове. Чтобы избежать подобных ошибок, надо всегда использовать кавычки в тех случаях, когда требуется сказать что-то о выражениях языка. Предложение «"Стул" – это существительное» построено правильно. Если же пренебречь кавычками, мы рискуем получить довольно нелепый вывод:

Стул – это существительное.

Некоторые стулья имеют четыре ножки

Некоторые существительные имеют четыре ножки.

Принцип взаимозаменимости: при замене имен с одинаковым значением, предложение, в котором эта замена осуществляется, не должно изменять свое истинностное значение (истинное предложение должно оставаться истинным, а ложное – ложным).

Пусть дано предложение «Земля вращается вокруг Солнца». Заменим «Солнце» на «центральное тело Солнечной системы». Очевидно, что значения этих выражений совпадают. В результате такой замены из истинного предложения получаем другое истинное предложение: «Земля вращается вокруг центрального тела Солнечной системы».

Принцип взаимозаменимости кажется самоочевидным, однако существуют языковые контексты, в которых замена равного равным приводит к противоречию. Рассмотрим предложение «Птолемей считал, что Солнце вращается вокруг Земли». Он считал, что это истинно. Проверим это. Заменим слово «Солнце» на выражение «центральное тело солнечной системы», имеющее то же значение. Получим заключение: «Птолемей считал, что центральное тело солнечной системы вращается вокруг Земли», которое является абсурдным.

В логике подобные ситуации известны как «антиномии отношения именования» – они возникают, когда некий объект известен (приятен, доступен и т.д.) субъекту в одном аспекте, и неизвестен (неприятен, недоступен и т.д.) в другом. Отсюда порой проистекает кажущаяся несовместимость двух обозначений одного и того же объекта.

Как же сохранить принцип взаимозаменимости и избежать антиномий? Следует различать два способа употребления языковых выражений. Первый – экстенсиональный, при котором выражения просто выделяют предметы. Второй – интенсиональный: предметы, обозначаемые выражениями, рассматриваются в определенном смысле, аспекте (показателем чего могут служить так называемые эпистемические операторы – слова «знает» «верит», «ищет», «думает» и т.п.). Если выражение употребляется в определенном аспекте, то его можно заменить другим выражением с тем же значением, только если во втором выражении предметы рассматриваются в том же аспекте.

Язык и табличное построение КЛВ. Таблица истинности.

А,в

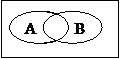
(4) А противоречит В(5) А дополняет В(6) А и В перекрещиваются

летат. аппарат легче/тяжелее воздуха рос.город,расплож. западнее байкала/ студент 1 курса,студ-т изуч. логику

(несовместимы,исчерпывают) восточнее урала (совместимы,исчерпывают) (совместимы,не исчерпывают)

А В А В

27.Логические отношения между сложными суждениями.

В процессе построения отношений между суждениями можно выделить сравнимые и несравнимые. Сравнимые суждения имеют общий субъект и предикат. Несравнимые суждения не имеют общего субъекта и предиката. Они делятся на: совместимые и несовместимые.

Несовместимыми называются суждения, у которых из истинности одного из них необходимо следует ложность другого, то есть эти суждения не могут оказаться одновременно истинными. Например, числа 1,2,3,4,… являются несовместимыми.

Совместимые суждения выражают одно и то же высказывание полностью или частично, поэтому могут быть одновременно истинными. К ним относятся отношения: эквивалентности, подчинения и субконтрарности (частичного совпадения).

Эквивалентность означает, что суждения совместимы по истинности, совместимы по ложности и из первого следует второе и наоборот.

Подчинение означает, что суждения совместимы по истинности, совместимы по ложности, из первого следует второе, но не наоборот.

Субконтрарность означает,что суждения совместимы по истинности, но не совместимы по ложности и логического следования нет.

Между логическими суждениями, высказываниями (с одинаковыми терминами) можно установить четыре типа отношений. В период Средневековья логики наглядно изображали их с помощью так называемого «логического квадрата»:

Aконтрарность Е

п е

п р и п

о о ч о

д т е д

ч и р ч

и в о и

н в о н

е и р е

н т е н

и о ч и

е р и е

п е

IсубконтрарностьО

Рассмотрим эти отношения между суждениями с помощью логического квадрата. В отношении подчинения находятся суждения форм A и I, а также суждения E и O. Например, общеутвердительное суждение «Все студенты первого курса изучают историю» является подчиняющим, а частноутвердительное суждение «Некоторые студенты первого курса изучают историю» является подчиненным.

Отношения субконтрарности (частичное совпадение)) имеет место между суждениями форм I и O, если они имеют одинаковые субъекты и одинаковые предикаты. Они являются совместимыми по истинности, но несовместимыми по ложности. Например, частноутвердительное суждение «Некоторые студенты-первокурсники занимаются в научных кружках» и частноотрицательное суждение «Некоторые студенты-первокурсники не занимаются в научных кружках». Оба суждения могут быть одновременно истинными, но ложными одновременно не могут быть.

Отношения несовместимости имеют место между отношениями контрарности (противоположность) и контрадикторности (противоречие). При этом контрарностьпоказывает отношения между суждениями форм A и E, которые совместимы по ложности, но не совместимы по истинности. Например, не могут быть одновременно истинными два суждения: «Все студенты учебной группы изучают китайский язык» и «Ни один студент учебной группы не изучает китайский язык».

Отношения котрадикторности имеют место между суждениями A и O, а также E и I. Они не совместимы по истинности и по ложности. Например, общеутвердительное суждение «Все люди обладают сознанием» и частноотрицательное суждение «Некоторые люди не обладают сознанием». Эти суждения не могут быть одновременно истинными и ложными. Также пример для общеотрицательного суждения «Ни один студент не может быть профессором» и частноутвердительного суждения «Некоторые студенты являются профессорами».

А, В А В А В

(4) А противоречит В (5) А дополняет В (6) А и В перекрещиваются

А В А В А В

Помимо булевых операций, к понятиям часто применяются такие операции обобщение и ограничение. Они основаны на отношении типа «род-вид». Из двух непустых понятий одно считается родовым, а другое видовым, если второе находится в отношении подчинения к первому. Это отношение на формальном языке обозначается символом « Ì».

Например, из двух понятий aА(a) «европейский город» и aВ(a) европейская столица» первое является родовым, а второе – видовым. То есть, В Ì А.Интересно, что содержания этих понятий находятся в обратном отношении, а именно, содержание aА(a) является частью содержания понятия aВ(a). Этот факт известен в логике как закон обратного отношения.

Закон обратного отношения: объем понятия aА(a)составляет часть объема понятияaВ(a),если и только если содержание понятияaВ(a)является частью содержания понятияaА(a).На формальном языке: А Í В º А(a) É В(a)

Сравним, например, два понятия:

1) «студент, сдавший все экзамены» и

2) «студент, сдавший хотя бы один экзамен»

Объем первого понятия включается в

объем второго (среди студентов, сдавших

хотя бы один экзамен, есть такие, кто сдал

все экзамены). А вот содержания этих

понятий находятся в обратном отношении:

из содержания первого (сдать все экзамены)

логически следует содержание второго (сдать

хотя бы один экзамен).

Обобщением называют переход от видового понятия к родовому (то есть, от понятия с меньшим объемом и большим содержанием, к понятию с большим объемом и меньшим содержанием). Для непустых понятий пределом обобщения является универсальное понятие.

Например: «мужчина, который является президентом России» → «мужчина, живущий в Кремле» → «мужчина, живущий в Москве» → «мужчина, живущий в России» → «мужчина, живущий в деревне» → «мужчина»

Ограничением называют переход от родового понятия к видовому (то есть, от понятия с большим объемом и меньшим содержанием, к понятию с меньшим объемом и большим содержанием). Для непустых понятий пределом ограничения является единичное понятие.

Например: «человек» → «человек, живущий в Европе» → «человек, живущий в Москве» → «человек, живущий в ЗАО Москвы» → «человек, являющийся нынешним префектом ЗАО Москвы».

31. Дедукция и индукция как способы познания.

Индукция (лат. inductio — наведение) — процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не строго через законы логики, а скорее через некоторые фактические, психологические или математические представления.

Дедукция(лат. deductio — выведение) — метод мышления, при котором частное положение логическим путем выводится из общего, вывод по правилам логики; цепь умозаключений (рассуждений), звенья которой (высказывания) связаны отношением логического следования.

Довольно часто в логике применяются способы умозаключения, приводящие к получению принципиально новой информации. При этом мы используем имеющиеся в посылках сведения как «подсказку», «намек», наводящий на мысль о возможности принятия некоторого умозаключения. Высказывание в этом случае строится следующим образом: если информация, содержащаяся в посылках A₁, …, A_n верна, то правдоподобно было бы считать, что верно и В.

A₁, …, A_n ú»В

Такие умозаключения получили название индуктивных (от лат. «inductio» – «наведение»), или правдоподобных.

К числу правдоподобных умозаключений относятся собственно обобщающая индукция, методы установления причинных зависимостей (исключающая индукция) и аналогия.

Под обобщающей индукцией понимаются такие умозаключения, в которых переходят от знания об определенных предметах некоторого класса к знанию обо всех предметах этого класса, то есть от единичных или частных утверждений к общим. Различают полную и неполную индукцию.

Полная обобщающая индукция – это умозаключение от знания об отдельных предметах некоторого класса, при условии исследования каждого предмета, входящего в этот класс, к знанию обо всех предметах этого класса. Полная индукция, по методу обоснования вывода, делится на: математическую и эмпирическую.

Математическая индукция – способ рассуждения, который часто используется в дедуктивных науках (логике и математике). Он применяется в тех случаях, когда исследуемый класс S задан индуктивным определением. Как вы помните, индуктивное определение состоит в том, что первоначально некоторые объекты прямо объявляются принадлежащими данному классу S. Все же остальные объекты порождаются из исходных с помощью каких-либо процедур f₁…f_n. Чтобы доказать наличие у всех предметов класса S свойства Р, применяют следующую схему рассуждения:

1. х₁ есть P базис индукции

2. S = {х₁, f₁(х₁), …, f_n(х₁)} индуктивное определение класса S

3. "х"f_j (х есть P) É (f_j(х) есть Р) индуктивный шаг

SaP индуктивное обобщение

Допустим, нам надо доказать, что все четные числа делятся на два. Воспользуемся индуктивным определением класса четных чисел: (1) 2 есть четное число, (2) все остальные четные числа получаются с помощью применения к двойке операций «f₁(x) = х+2» или «f₂(x) = х–2» n-го числа раз. Базис индукции очевиден: 2 делится на два. Индуктивный шаг состоит в том, что если некое число х делится на два, то х+2 и х–2 тоже делятся на два. Вывод: все четные числа делятся на два.

Математическая индукция дает достоверное знание. Всеобщность вывода определяется здесь знанием законов порождения исследуемого класса объектов.

Полная эмпирическая индукция достигает всеобщности вывода другим путем – сплошной эмпирической (опытной) проверкой исследуемого класса. Логическая схема этого способа рассуждения такова:

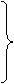1. x₁ есть P

2. x₂ есть P

. эмпирические факты о классе М ={x₁, …, x_n}

.

.

n. x_n есть P

n+1. M = S

SaР индуктивное обобщение

Достоверность заключения по полной обобщающей эмпирической индукции определяется тем, что условная вероятность вывода при данных посылках равна 1. Ведь множество исследованных предметов М совпадает с классом S, о котором идет речь в заключении, а при m = s величина 1/2^s-mравняется единице.

Полная эмпирическая индукция является ограниченным познавательным приемом. Во-первых, она может применяться лишь в тех случаях, когда класс S конечен и легко обозрим. Чтобы доказать полной индукцией, что все рыбы дышат жабрами, пришлось бы выловить всех рыб, а это в принципе невозможно.

Во-вторых, даже если класс S конечен, сплошная его проверка иногда требует таких огромных затрат, на которые общество не может пойти. Например, для установления того, что все граждане страны испытывают единодушное согласие по поводу какого-то важного государственного вопроса, можно провести поголовное голосование – референдум. Однако эта процедура требует больших затрат времени, материальных и людских ресурсов.

Как в теории, так и на практике возникают различные причины, по которым сплошная проверка бывает невозможной. В таких случаях применяется процедура неполной обобщающей индукции. Обобщающая индукция называется неполной, если в ней осуществляется частичная проверка предметов исследуемого класса.

Неполная обобщающая индукция делится на: популярную и научную. Схема популярной индукции имеет следующий вид:

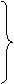1. x₁ есть P

2. x₂ есть P

. эмпирические факты о классе М ={x₁, …, x_n}

.

.

n. x_n есть P

n+1. MÌ S

SaР индуктивное обобщение

Отличие популярной индукции от полной состоит в n+1-ой посылке. При полной индукции класс М в точности совпадает с классом S. При индукции популярной он составляет лишь часть этого класса. Ясно, что истинность заключения в данном случае является проблематичной. Ведь среди непроверенных предметов из S могут быть и такие, которые свойством Р не обладают.

Пример ложного заключения, полученного посредством популярной индукции, – предложение «Все волки серы».

Рассматриваемое рассуждение называется популярной (народной) индукцией в силу своей наивной простотой. Эта простота проявляется прежде всего в том, что на наличие свойства Р проверяются первые попавшиеся объекты. После чего проводится поспешное обобщение – типичная ошибка индуктивного рассуждения. Однако вывод по неполной индукции можно существенно усовершенствовать и добиться повышения степени правдоподобности получаемых результатов.

Научная индукция проверяет на наличие свойства Р не первые попавшиеся предметы класса S, а те из них, которые специально отобраны для этой цели. При этом весь исследуемый класс S называют генеральной совокупностью, а множество отобранных из него образцов – выборкой. Выборка подвергается сплошной проверке, а затем полученный результат переносится на всю генеральную совокупность.

Для надежного обоснованиятакого переноса требуется, чтобы выборка была репрезентативной. Это означает, что выборка должна достаточно точно передавать структуру класса S, разнообразие его состава, и в частности, те его особенности, которые могут влиять на отсутствие свойства Р. В таких случаях условимся говорить, что М репрезентирует S, сокращенно M @ S. Схема научной индукции такова:

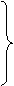1. x₁ есть P

2. x₂ есть P

. эмпирические факты о классе М ={x₁, …, x_n}

.

.

n. x_n есть P

МaР полная индукция

n+1. M @ S утверждение о репрезентативности выборки

SaР индуктивное обобщение

Добиться репрезентативности выборки можно двумя различными способами. Первый способ основан на выдвижении некоторых гипотез о том, в силу каких причин у предметов исследуемого класса может отсутствовать свойство Р. Например, если проверяется доброкачественность партии молочных продуктов, то отсутствие этого свойства (недоброкачественность) может зависеть от срока хранения продукта, от условий его хранения, от того, какое предприятие выпустило продукцию, и других параметров. Именно такие «подозрительные» образцы включаются в выборку и подвергаются проверке. Если гипотезы точно фиксируют все случаи, в силу которых продукция может оказаться недоброкачественной, и если в генеральной совокупности S таковая имеется, то в выборку обязательно попадет какое-то ее количество.

У данного метода два недостатка. Первый связан с тем, что у нас могут отсутствовать хоть какие-то разумные гипотезы для объяснения свойства Р. Второй же состоит в том, что мы можем по тем или иным причинам упустить какой-то важный параметр, от которого зависит отсутствие свойства Р. Тем самым будет делаться определенная систематическая ошибка, которая и приведет к неверным результатам.

Чтобы исключить эти недостатки, применяют второй способ формирования выборки, порождая ее чисто случайным образом. Для этого используют специальные таблицы случайных чисел. Но чтобы такая случайная выборка оказалась репрезентативной, она должна быть достаточно объемной. Согласно закону больших чисел, закономерности, которым подчиняются массовые явления, обнаруживаются лишь при достаточно большом числе наблюдений.

Виды понятий по содержанию

По типу признаков понятия подразделяют на:

а)– Положительнымсчитается понятие, в котором предметы обобщаются на основании признака, которым они обладают (например, «учебник, купленный в книжном магазине»).

– Отрицательнымсчитается понятие, в котором предметы обобщаются на основании признака, которым они не обладают (например, «студент, не знающий японский язык»).

б)– Относительнымсчитается понятие, в котором предметы обобщаются на основании их отношения к другим предметам. Например, относительным является понятие о жене – «женщина, состоящая в браке с каким-то мужчиной», – поскольку его признак выделяет женщин не по их собственным качествам, а через отношение к каким-то мужчинам, то есть как одну из сторон супружеской четы.

– Безотносительнымсчитается понятие, в котором предметы обобщаются на основании их собственных свойств. Например, понятия о композиторе – «человек, сочиняющий музыку».

В заключении отметим, что осуществить полный логический анализ понятия, значит определить его универсум (род), объем и содержание, а также установить, к каким видам оно относится по всем указанным выше основаниям деления.

Исчисление высказываний. Правила вывода.

Исчисление – это сугубо формальная теория, содержание которой фиксируется на специально созданном символическом языке, а все рассуждения строятся как преобразования одних символов в другие по определенным правилам.

Правила вывода[1]:

Правила введения связок	Правила исключения связок
Øв	В, ØВ ØС*	Øи	ØØА А
&в	А,В А&В	&и	А&ВА&В А В
Úв	А В . АÚВ АÚВ	Úи	АÚВ, ØААÚВ, ØВ В А
Éв	В . С*ÉВ	Éи	АÉВ, А В

* где С – последнее допущение

Данные правила представляют собой схемы разрешенных в логике высказываний преобразований. Например, правило (&_в)разрешает от утверждения двух отдельных формул А и В перейти к утверждению более сложной формулы А&В, и так далее (смысл большинства правил будет ясен любому, кто помнит табличные определения соотвествующих связок).

В комментариях нуждаются лишь два правила: введение отрицания (Ø_в) и введение импликации (É_в). Как вы поняли, формула С, фигурирующая в них, обозначает не любое высказывание, а именно последнее допущение. Дело в том, что допущения (гипотезы, версии) довольно часто применяются в построении дедуктивных рассуждений, играя в них вспомогательную роль. И как раз для того, чтобы оценить эту роль, подвести итог рассмотрению того или иного предположения, нужны правила введения отрицания и введения импликации.

Возьмем, например, правило (Ø_в). Над чертой стоят две формулы, противоречащие друг другу: ВиØВ. Это значит, что в какой-то момент наших рассуждений мы пришли к двум взаимоисключающим выводам. Отчего такое могло случиться? Видимо, мы исходили из какого-то ложного допущения (С), и его следует отрицать. В том случае, если допущений было несколько, естественно отрицать последнее из них (если после этого противоречие остается, используем правило (Ø_в) еще раз, и так далее до обнаружения ошибочной посылки). Рассмотрим пример правила введения отрицания:

Предположим, что Земля квадратная. (С)

Тогда тень, отбрасываемая ею, тоже должна быть квадратной. (В)

Но тень Земли на Луне во время лунного затмения – круглая. (ØВ)

Предположение неверно, т.е. Земля не является квадратной (ØС)

Рассмотрим правило введения импликации. Оно применяется в тех случаях, когда используемое допущение не приводит к явному противоречию, так что вместо двух взаимоисключающих суждений мы получаем одно, вполне ясное и непротиворечивое (В). Можем ли мы утверждать его как очевидную и незыблемую истину? Нет, ведь оно получено с использованием допущения (С), которое само по себе еще не доказано. Но мы вправе утверждать, что по крайней мере суждение В вытекает из упомянутого допущения (СÉВ), то есть В истинно при условии истинности С. Например:

Предположим, число х кратно четырем. (С)

Четыре кратно двум.

Получается, х кратно числу, которое кратно двум.

Значит, х тоже кратно двум. (В)

Итак: если число х кратно четырем, то оно кратно и двум. (СÉВ)

Выводом называется непустая конечная последовательность формул, удовлетворяющая условиям:

1.Каждая из них либо является посылкой, либо получена из предыдущих формул по одному из правил вывода;

2. Если в выводе применялись правила (É_в) или (Ø_в), то все формулы, начиная с последней посылки и вплоть до результата применения данного правила, исключаются из участия в дальнейших шагах вывода

Последнее требование означает, что эти формулы уже были использованы и возвращаться к ним более нельзя. Почему? Если использовалось правило (Ø_в), значит в выводе фигурировало заведомо ложное допущение, из которого было получено противоречие. Очевидно, что делать из него еще какие-либо умозаключения, равно как и использовать уже сделанные, абсурдно. Если же речь идет об использовании правила (É_в), то мы понимаем, что в выводе фигурировало допущение C, позволившее получить некоторую нужную нам формулу B, но само по себе еще не доказанное. Возвращаться к этому допущению (или к формулам, из него выведенным) означало бы выдавать гипотетическую истинность В (при условии С) за категорическую. Это может привести к ошибке под названием «круг в доказательстве».

Формулы, исключенные из дальнейшего хода рассуждения после применения правила (É_в) или (Ø_в), называются подвыводом. Это значит, что они были полезны лишь внутри какого-то вывода, но не обязательно являются истинными сами по себе. Стоит заметить, что в сложных рассуждениях могут встречаться не только подвыводы, но и подвыводы внутри подвыводов, и так далее. Таким образом, процедура построения вывода как бы разбивается на несколько подчиненных один другому блоков, объединенных одной общей целью. Поэтому изложенная здесь логическая теория называется системой субординатного (т.е. подчиненного) вывода.

Рассмотрим пример рассуждения, производимого с помощью системы субординатного вывода. (В дальнейшем тот факт, что некоторые формулы в выводе являются исключенными, будем обознача