Разбиение множества на классы по одному , двум и трем свойствам

Определение 16.1. Разбить множество на классы – это значит представить его в виде объединения непересекающихся подмножеств.

Множество, которое мы собираемся разбить на классы в соответствии со свойствами его элементов, удобно представлять себе в виде универсального множества и , соответственно, обозначать его через U .

а) Допустим вначале, что существует одно-единственное свойство (свойство №1), которым элементы нашего множества U могут обладать или не обладать. Обозначим через А подмножество нашего универсального множества, состоящее из всех элементов, обладающих свойством №1. Тогда A’ (т.е. дополнение множества А) будет , очевидно, состоять из всех элементов, не обладающих свойством №1. Таким образом, если в нашем распоряжении имеется только одно-единственное свойство, которым элементы могут обладать /не обладать, то максимальное возможное количество классов, на которые удастся разбить множество U , равно двум. (См. рис. 16.1). Заметим, что один из классов, на которые мы разбили множество U, может быть пуст.

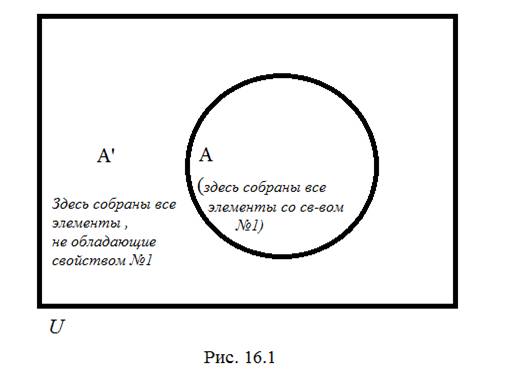
б) Пусть теперь в нашем распоряжении появилось второе свойство (свойство №2) которым (независимо от свойства №1) могут обладать/не обладать элементы из множества U. Обозначим совокупность всех элементов из U, обладающих свойством №2, через В. Из рис.16.2 видно, что максимальное количество классов, на которые может быть разбито множество U в соответствии с обладанием/не обладанием свойствами №1 и №2, равно четырем. (См. рис. 16.2). Как видно из рис. 16.2, IV класс состоит из всех элементов, обладающих свойством №2, но не обладающих свойством №1. Подчеркнем, что некоторые из изображенных на рис 16.2 классов могут быть пустыми.

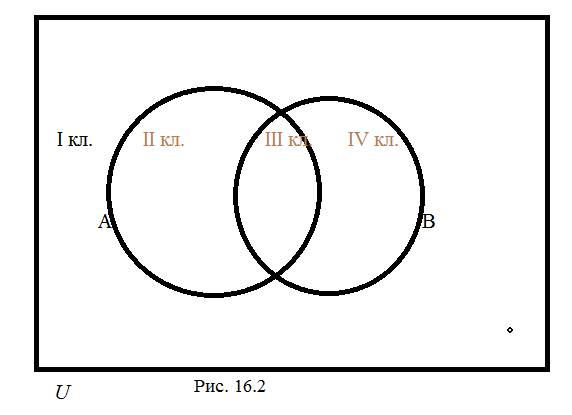
в) Если число свойств (в соответствии с наличием/отсутствием которых проводится классификация) равно трем, максимально возможное количество классов в нашей задаче оказывается равным восьми (см. рис.16.3).

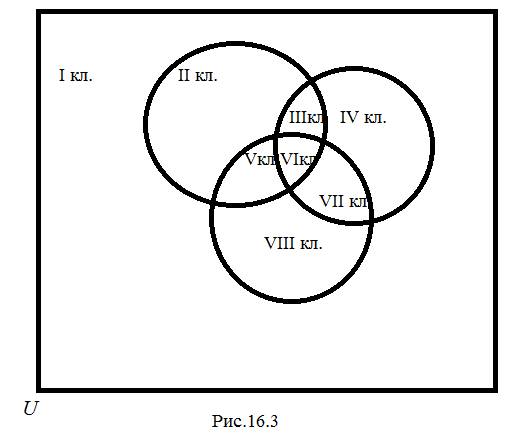
Глава 2. Элементы математической логики

Высказывания

Определение 1.1.Высказыванием называется любое повествовательное предложение, о котором можно определенно и однозначно сказать, что оно либо истинно, либо ложно.

Примеры высказываний:

1) «Петя кушает кашу».

2) «Луна – это апельсин».

3) «Дважды два пять».

4) «На каждой елке висят шоколадные конфеты».

5) «В учебнике математики 335 страниц».

Примеры предложений, не являющихся высказываниями:

1) «Мне немного не по себе». (Это повествовательное предложение не является высказыванием, так как неясно, что значит «не по себе» и в каком смысле следует понимать в этом предложении термин «немного».)

2) «Принеси, пожалуйста, кофе». (Это не повествовательное предложение.)

3) «Здравствуйте!» (Это не повествовательное предложение.)

4) «Как пройти на площадь Трех вокзалов?» (Это не повествовательное предложение.)

5) «Я очень рад». (Это повествовательное предложение не является высказыванием, так как невозможно в принципе проверить его истинность. Как отличить «очень рад» от просто «рад»?)

6) «Тише едешь, дальше будешь.» (Это повествовательное предложение представляет собой пословицу, которая не претендует на то, чтобы выражать истину во всех случаях жизни.)