Основные правила вывода, правила 1 и 2.

I. 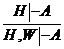.Это правило следует из того простого рассуждения, что если мы можем получить формулу A из совокупности Н, то из расширенной совокупности Н,W мы тем более получим формулу А.

II. 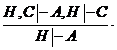Это почти очевидное правило мы, тем не менее, докажем. Так как по условию из совокупности формул Н,С выводима формула А, то существует вывод из Н,С, последней формулой которого является А:

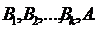(1)

Так как по условию из совокупности формул Н выводима формула С, то существует вывод из Н, последней формулой которого является С:

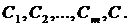(2)

Если в выводе (1) отсутствует формула С, то он является выводом

только из совокупности Н и, значит, А выводима из H.

Если же в выводе (1) одна из формул есть формула С, например формула 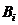, то, вставив между формулам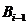и и 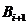вывод формулы (2), являющейся выводом из Н, в результате получим вывод из Н, С

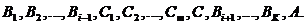(3)

Так как в вывод (3) входит вывод (2) из Н, а в оставшуюся часть вывода

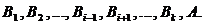(4)

Формула С не входит, то вывод (4) является выводом только из Н.

На основании же свойства 2 вывода вывод (3) тоже будет выводом только из Н. Поэтому и в этом случае формула А выводима из Н, что и требовалось доказать.

Основные правила выводимости. 3 и 4 .

Ш.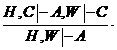

Доказательство. Так как 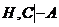, то по правилу I имеем 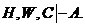Так как 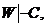то также по правилу I имеем 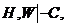. Используя теперь правило II, получаем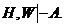

Для правил выводимости II и III можно предложить более простые и компактные доказательства. Докажем правило II, воспользовавшись следующими соображениями. Запись 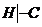означает, что для того, чтобы вывести С, нужно иметь совокупность формул Н. Значит, в записи 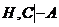одну формулу С можно заменить на совокупность формул Н, поэтому можно записать: 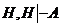. Но дважды используемое одно и то же множество Н есть, очевидно, одно множество Н. То есть верна формула 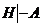, а это и требовалось доказать.

Правило выводимости III доказывается аналогичным образом с той лишь разницей, что здесь не приходится заменять дважды используемое одно и то же множество на одно множество. Заменим в 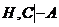множество С на W, тогда 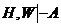что и требовалось доказать.

Подобным образом можно доказать также частный случай для правила выводимости III, т.е.

III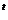

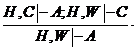
Доказательство. Заменим в 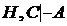множество С на Н,W, тогда 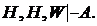Но совокупность множеств Н, Н есть одно множество Н, т.е. 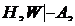что и требовалось доказать.

IV.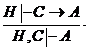

Доказательство. Так как из Н выводима формула 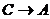, то существует вывод из Н, конечной в котором является формула :

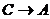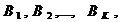
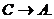(1)

Присоединим теперь к совокупности формул Н формулу С. Получим совокупность формул Н, С. Добавляя на основании пункта 1 понятия вывода к выводу (1) формулу С, мы получим вывод

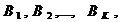
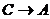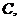, (2)

который является выводом из Н, С.

Но в конец вывода (2) можно дописать формулу А, которая получается из формул С и 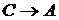согласно ПЗ (пункт 3) понятия вывода. Отсюда имеем вывод из совокупности Н, С

,

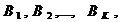
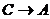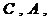
последней формулой которого является формула А. Значит, 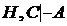, что и требовалось доказать.