Проблемы аксиоматического исчисления высказываний. Проблема разрешимости и непротиворечивости.

Всякая аксиоматическая теория для своего обоснования требует рассмотренных четырех проблем:

1) проблемы разрешимости,

2) проблемы непротиворечивости,

3) проблемы полноты,

4) проблемы независимости.

1. Проблема разрешимости исчисления высказываний заключается в доказательстве существования алгоритма, который позволил бы для любой заданной формулы исчисления высказываний определить, является она доказуемой или нет.

Теорема 1. Проблема разрешимости для исчисления высказываний разрешима.

2. Суть проблемы непротиворечивости исчисления высказываний состоит в следующем. Логическое исчисление называется непротиворечивым, если в нем недоказуемы никакие две формулы, из которых одна является отрицанием другой.

Иначе говоря, аксиоматическое исчисление называется непротиворечивым, если в нем не существует такая доказуемая формула А, что наряду с ней доказуема и формула .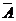

Теорема 2. Исчисление высказываний непротиворечиво.

17. . проблемы аксиоматического исчисления высказываний. Проблема полноты и независимости.

3. Проблема полноты исчисления высказываний. Существует два понятия полноты − в узком смысле и в широком смысле.

Аксиоматическое исчисление называется полным в узком смысле, если добавление к списку его аксиом любой недоказуемой в исчислении формулы в качестве новой аксиомы приводит к противоречивому исчислению.

Исчисление высказываний называется полным в широком смысле, если любая тождественно истинная формула в алгебре логики доказуема в исчислении высказываний.

Теорема 3. Исчисление высказываний полно в узком смысле.

Теорема 4. Исчисление высказываний полно в широком смысле.

4. Проблема независимости аксиом исчисления высказываний. Для каждого аксиоматического исчисления возникает вопрос о независимости его аксиом; а именно: нельзя ли какую-нибудь аксиому вывести из остальных аксиом, применяя правила вывода?

Если для некоторой аксиомы это возможно, то ее можно исключить из списка аксиом системы, и возможности логического исчисления при этом не изменятся. Иначе говоря, класс доказуемых формул не изменится.

Аксиома называется независимой от всех остальных аксиом исчисления, если она не может быть выведена из остальных аксиом.

Система аксиом исчисления высказываний называется независимой, если каждая аксиома системы независима.

Теорема 5. Система аксиом исчисления высказываний независима.

Понятие предиката, определённого одноместного предиката. Множество истинности предиката. Тождественно истинный предикат. Примеры предикатов.

Логика предикатов расчленяет простое высказывание на субъект (подлежащее, дополнение) и предикат (сказуемое, определение).

Субъект – это то, о чем что-то утверждается в высказывании. Предикат – это то, что именно утверждается о субъекте. Например, в высказывании “12 – составное число” “12” – субъект, “ составное число” – предикат. Это высказывание утверждает, что “12” обладает свойством быть составным числом.

Определение 1. Одноместным предикатом 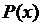называется произвольная функция переменной 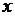, определенная на некотором множестве 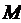и принимающая значения из множества .

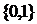Множество 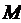, на котором определен предикат 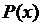, называется областью определения предиката.

Множество всех элементов 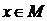, при которых предикат 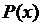принимает значение “истина”, называется множеством истинности этого предиката. Символически множество истинности предиката 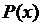записывают так: 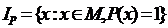. Эта запись означает, что множество 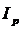состоит из элементов, обладающих свойством, указанным после двоеточия.

Определение 2.Предикат 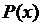, определенный на множестве 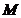, называется тождественно истинным (тождественно ложным), если .

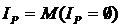Обобщением понятия одноместного предиката является понятие 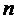-местного предиката, с помощью которого выражается отношение между 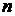предметами.

Понятие Н местного предиката. Двухместного предиката. Пример бинарного предиката. Декартово произведение 2 множеств.

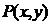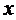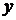Определение 3. Двухместным предикатом называется функция двух переменных и , определенная на множестве 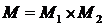и принимающая значение из множества 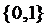. Примерами двухместных предикатов являются: предикат равенства 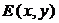─ “ 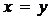”, определенный на множестве действительных чисел 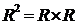, предикат делимости нацело 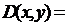” ”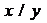, определенный на множестве .

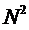Таким образом, предикат – это функция или, как мы уже говорили выше, высказывательная форма. Если, например, в высказывательную форму 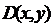мы подставим вместо 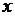и 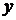какие-то конкретные значения, то высказывательная форма становится высказыванием, принимающим вполне определенные значения истины или лжи (1 или 0). Так, 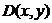есть предикат (высказывательная форма), но 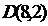уже является истинным высказыванием, а 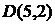− ложным высказыванием. В то же время 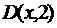является высказывательной формой (предикатом), так как его значение истинности зависит от того, каким натуральным числом будет заменена переменная 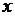(т.е. является функцией от 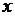, а значит, предикатом). В то же время 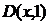является высказыванием, причем истинным, так как любое 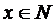делится на единицу.

Еще несколько замечаний о терминологии. Иногда вместо термина “ 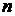-местный предикат” употребляют термин “ 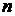-арный предикат”. При 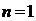этот предикат называется унарным (от лат. unio ─ единение, единый), при 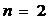− бинарным (от лат. binaries − двойной) и при 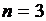− тернарным (от лат. tertia – третья).

Для общности еще вводят понятие 0-арного предиката, под которым понимается любое истинное или ложное высказывание. Такое определение логично, если вспомнить, что в определении высказывания нет переменной, а в определении предиката она есть. Тогда некоторое предложение мы можем называть 0-арным предикатом, если в нем отсутствуют переменные.