Тема: Минимизация логического выражения и составление логических и релейных схем
Цель работы–научитьсямоделировать логические функции при помощи логических элементов.
Рабочее задание
1. Домашнее задание
1.1. В соответствии с заданным вариантом задания (табл. 8) на основании таблицы истинности (табл. 9) записать логические выражения для двух переключательных функций (и минимизировать их с помощью диаграмм Вейча путем преобразования выражений для переключательных функций с помощью формул и тождеств.
Таблица 8
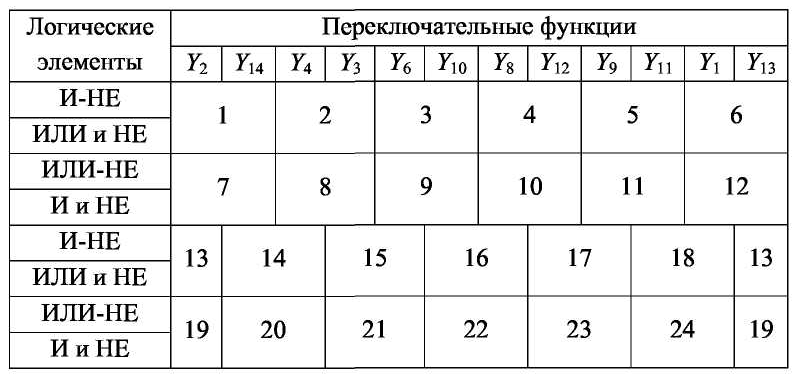
1.2. Получить логические выражения из п. 1.1, используя диаграммы Вейча.
1.3. На базе логических элементов И, ИЛИ, НЕ выполнить две функциональные схемы, реализующие заданные логические выражения до минимизации. Нарисовать временные диаграммы работы указанных схем.
1.4. На базе заданных логических элементов, в зависимости от варианта (табл. 8) выполнить четыре функциональные схемы, реализующие заданные логические выражения до и после минимизации. Нарисовать временные диаграммы работы указанных схем.
Экспериментальная часть
2.1. Запустить пакет Electronics Workbench. Смоделировать функциональные схемы, разработанные в п.п. 1.3-1.4. Примеры, графических схем проектирования функции дизъюнкции на базе элементов И, ИЛИ, НЕ в программе Electronics Workbench приведен на рисунке 3, а на базе элементов И-НЕ – на рисунке 4.
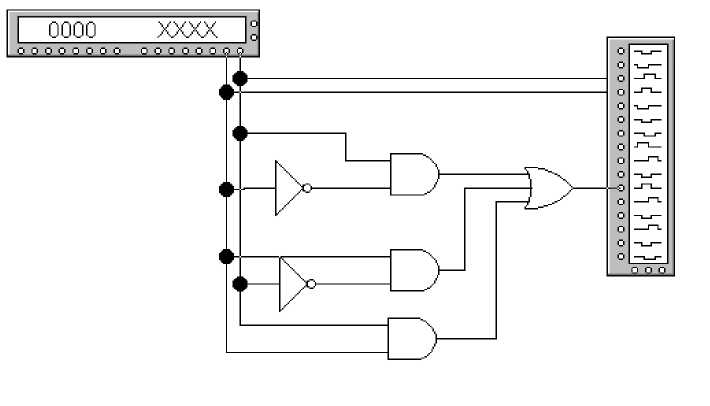
Рисунок 3
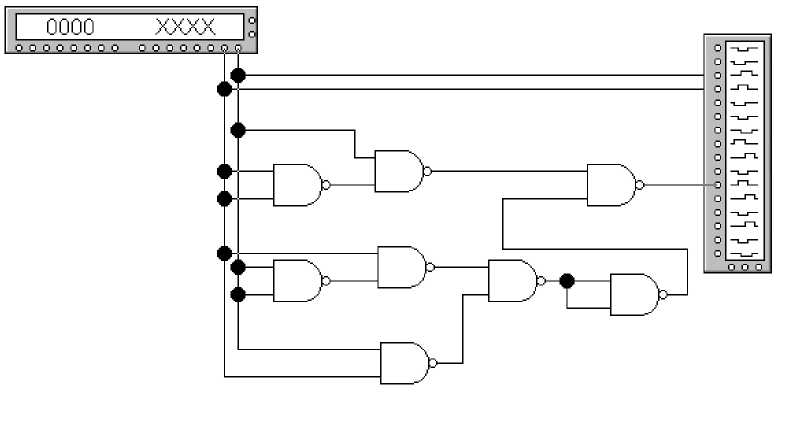
Рисунок 4
2.2. Для имитации работы спроектированной схемы подключить ее входы к генератору слов Word Generation, расположенному на панели компонентов Instruments.
2.3. Получить диаграммы входных и выходных сигналов на экране логического анализатора Logic Analizer, расположенного на панели компонентов Instruments.
Пример, диаграммы входных и выходных сигналов для функции дизъюнкции приведен на рисунке 5.
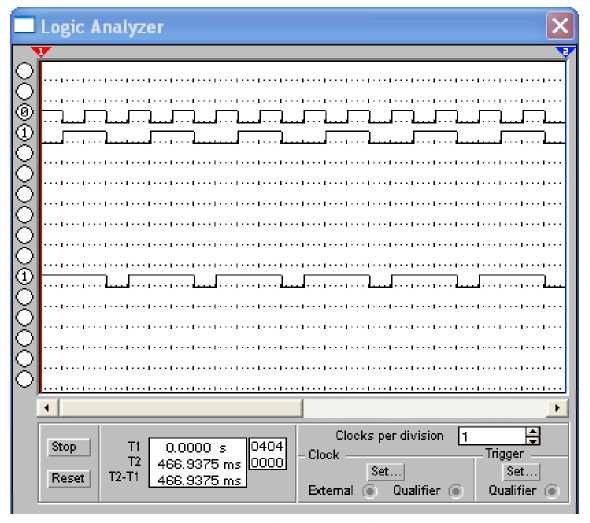
Рисунок 5
Обработка экспериментальных данных
3.1. Составить отчет о выполнении лабораторной работы. Включить в отчет логические выражения, полученные на основании таблицы истинности, и результаты минимизации на основании диаграммы Вейча.
3.2. Включить в отчет распечатки построенные схемы и диаграммы входных и выходных сигналов для каждой из выполненных схем.
3.3. Сравнить диаграммы входных и выходных сигналов с таблицей истинности для каждой из моделируемых переключательных функций. Сделать выводы.
Методические указания
При проектировании узлов и устройств цифровых вычислительных машин широко используются методы анализа и синтеза логических схем, которые получили название методов логического проектирования. Они основаны на использовании алгебры логики или булевой алгебры. Основным понятием алгебры логики является высказывание – любое утверждение, в отношении которого имеет смысл говорить, что оно истинно или ложно. При этом считается, что каждое высказывание не может быть одновременно и истинно и ложно. Каждое высказывание можно обозначить определенным символом. Запись Xj = 1 означает, что высказанное истинно, а Xj = 0 – что высказывание ложно.
В алгебре логики высказывания могут быть простыми и сложными. Высказывание, значение истинности которого не зависит от значений истинности других высказываний, называется простым. При анализе и синтезе логических схем простое высказывание рассматривается как независимая переменная, принимающая два значения: 0 и 1. Высказывание Y(X1, X2, …, Xn), значение истинности которого зависит от значения истинности других высказываний, составляющих его, называется сложным и также может принимать два значения: 0 и 1.
При технической реализации переключательных функций переменные X1, X2, …, Xn отождествляются с входящими сигналами, поступающими на физическую схему, реализующую переключательную функцию, а значение Y(X1, X2, …, Xn) представляет собой выходной сигнал схемы. Совокупность значений n переменных называется набором.
Одной из распространенных форм задания переключательных функций является таблица истинности, где переменные X1, X2, …, Xn обычно располагаются в порядке возрастания двоичных чисел, образованных набором. Для переключательной функции n переменных существует m = 2n различных наборов, на которые она может принимать значение 0 или 1.
В таблице 9 приведен полный перечень функций двух аргументов. Функции, образованные логическими переменными, можно преобразовывать в соответствии с правилами или законами алгебры логики. При этом стремятся минимизировать логическое выражение, т.е. привести его к виду, удобному для практической реализации на логических элементах.
В электронных цифровых устройствах элементарные логические операции над двоичными переменными реализуются простыми логическими схемами, которые называются логическими элементами или вентилями. Число входов логического элемента соответствует числу переменных реализуемой им переключательной функции. В таблице 10 приведены названия переключательной функции двух переменных и логического элемента, реализующего эту функцию, а также условное обозначение элемента структурных и функциональных схем цифровых устройств. В последней графе этой таблицы даются некоторые названия логических элементов, которые встречаются в отечественной и зарубежной литературе.
Основное требование, предъявляемое к функционально полному набору логических элементов, состоит в том, чтобы с помощью этого набора можно было построить любую сложную логическую схему. Ввиду того, что законы функционирования элементов однозначно описываются переключательными функциями, применяя операцию суперпозиции, можно получить любую, сколь угодно сложную переключательную функцию.
Таблица 9
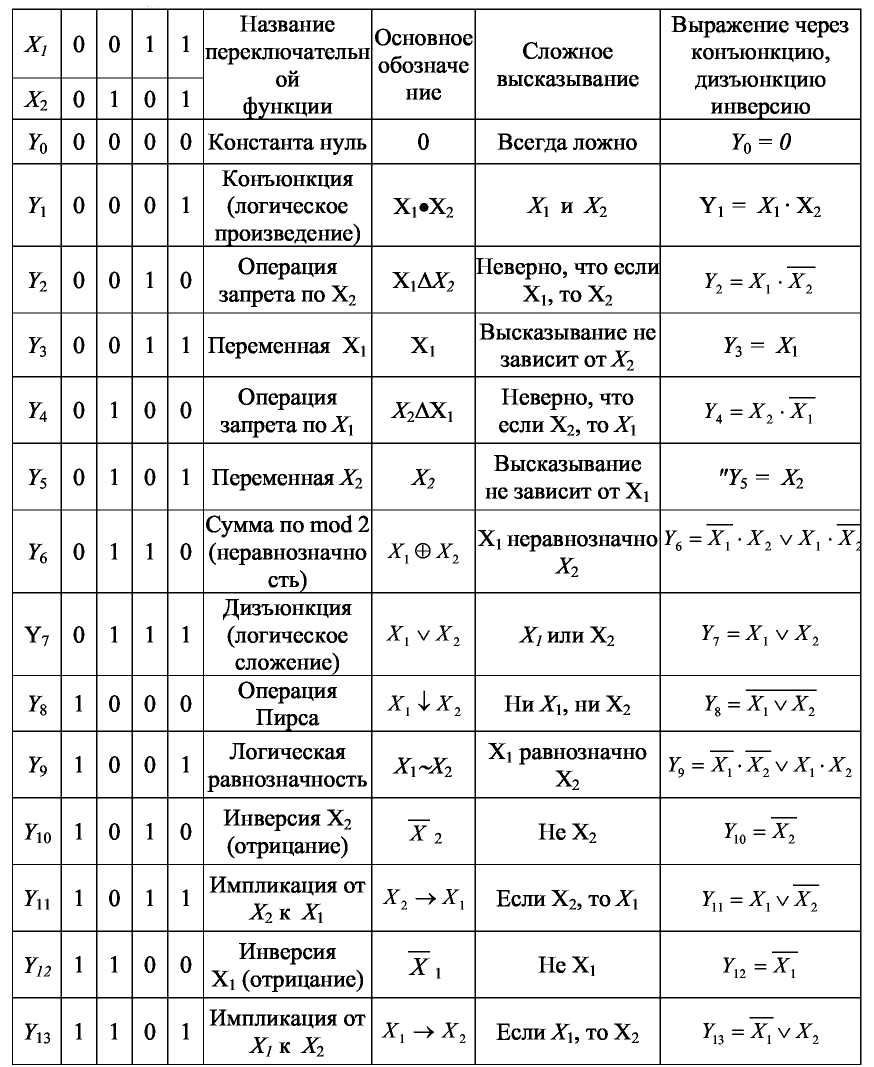

Таблица 10

Функционально полный набор переключательных функций является несократимым, если исключение любой функции набора нарушает его полноту. Такой набор можно состроить с помощью одной, двух, трех и четырех функции.
Примером полных несократимых наборов переключательных функций трех, двух и одной переменной могут служить:
· дизъюнкция, логическая равнозначность, константа нуль;
· конъюнкция, логическая неравнозначность, константа единица;
· конъюнкция и отрицание;
· дизъюнкция и отрицание;
· операция Пирса;
· операция Шеффера.
Однако наборы логических элементов и соответствующие им наборы переключательных функций, как правило, обладают функциональной избыточностью, например, широко используемый для построения логических схем цифровых устройств набор, состоящий из переключательных функций конъюнкции; дизъюнкции и отрицания, который реализуется логическими элементами И, ИЛИ, НЕ соответственно. Этот набор элементов дает возможность достаточно гибко и экономично строить схемы, например, на полупроводниковых приборах. Кроме того, с помощью этого набора функций наиболее просто перейти от широко распространенной записи переключательной функции в канонической форме к структурной схеме на логических элементах И, ИЛИ, НЕ, и др.
Задача логического проектирования на первом этапе полностью эквивалентна математической задаче представления заданной переключательной функции переключательными функциями выбранной функционально полной системы. При проектировании логических схем сначала необходимо записать переключательную функцию в определенной исходной форме: совершенная дизъюнктивная нормальная форма (СДНФ) и
совершенная конъюнктивная нормальная форма (СКНФ). Однако эти формы, как правило, достаточно сложные. Поэтому их минимизируют или с помощью диаграмм Вейча, или путем преобразования выражений для переключательных функций с помощью формул и тождеств, приведенных в таблице 11.
Например, для функции дизъюнкции логическое выражение на основании таблицы истинности (табл. 2) будет иметь вид:
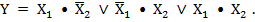
Таблица 11
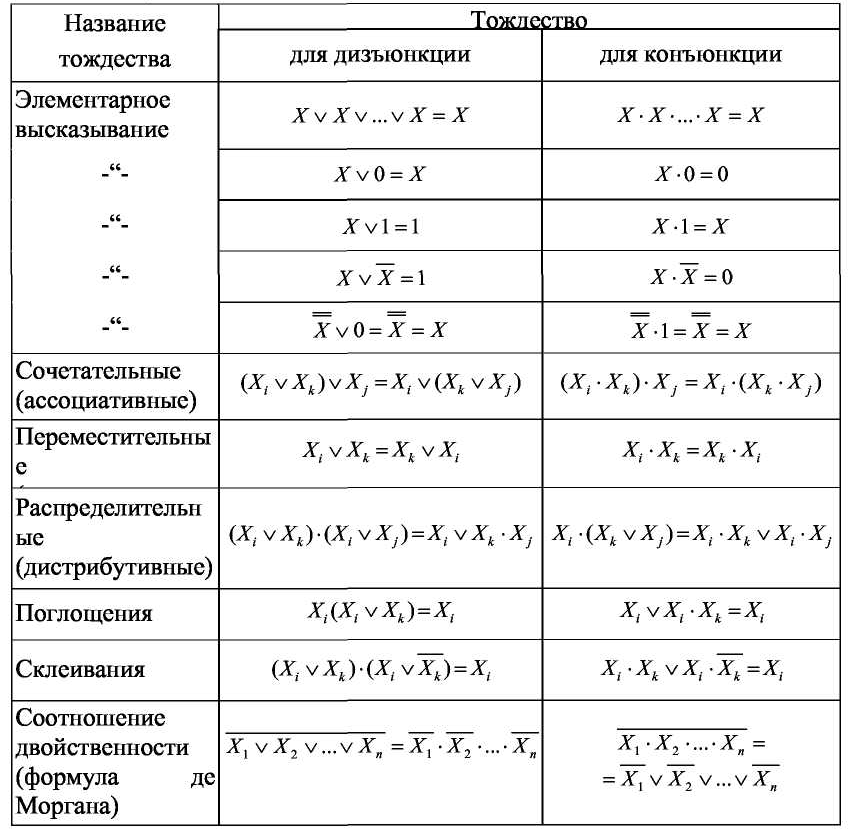
При минимизации на основании тождеств (табл. 11) получим следующее выражение:
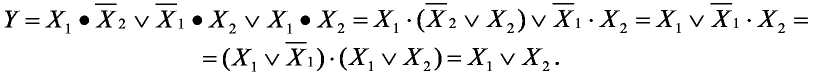
Если число логических переменных не превышает 5-6, минимизацию логических уравнений удобно производить с помощью карт Карно или диаграмм Вейча. Минимизацию проводят путем объединения наборов (термов) на карте Карно. Причем объединяемые наборы должны иметь одинаковые значения функции (все 0 или все 1).
Рассмотрим пример: требуется минимизировать логическую функцию двух переменных дизъюнкцию. На основании таблицы истинности (табл. 9) составим карту Карно изображенную на рисунке 5, в которой наименования столбцов и строк представляют собой значения переменных, причем переменные располагаются в таком порядке, чтобы при переходе к соседнему столбцу или строке изменялось значение только одной переменной.
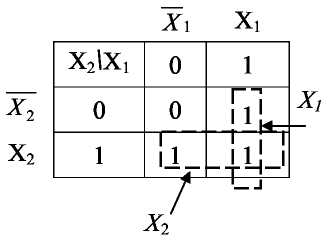
Рисунок 5
Таблицу заполняют значениями функции, соответствующими комбинациям значений переменных. На карте Карно отмечают группы, состоящие из 2n ячеек (n – число переменных) и содержащие 1, т.к. они описываются простыми логическими выражениями. Каждый группа объединяет две ячейки, соответствующие логическим преобразованиям:
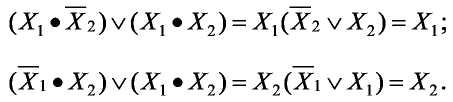
Компактное выражение, описывающее функцию, представляет собой дизъюнкцию логических выражений, полученных при помощи карт Карно. В результате получаем выражение в СДНФ, совпадающее с переключательной функцией дизъюнкции:
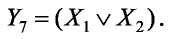
Контрольные вопросы
1. Какие функциональные схемы называют комбинационными?
2. Что представляет из себя таблица истинности для переключательных функций?
3. Какие требование, предъявляются к функционально полному набору логических элементов?
4. Почему штрих Шеффера обладает функциональной полнотой?
5. Чем отличаются схема исключающее ИЛИ и равнозначность?
6. Как осуществляется процесс синтеза цифровых логических схем?
7. С какой целью проводится минимизация булевых функций?
8. Каким образом маркируются интегральные микросхемы?
9. Как обозначаются ЛЭ на схемах электрических функциональных и принципиальных?
