Выражение суждения в виде формулы логики предикатов
Существуют две задачи, определяющие связь между суждениями и формулами логики предикатов:
1) выражение суждения в виде формулы логики предикатов;
2) интерпретация формулы логики предикатов.
Рассмотрим первую задачу.
Суждение – это мысль, в которой утверждается наличие или отсутствие свойств предметов, отношений между предметами.
Простым суждением назовем суждение, в котором нельзя выделить часть, в свою очередь являющуюся суждением. Среди простых суждений выделяют атрибутивные суждения и суждения об отношениях.
В атрибутивных суждениях выражается наличие или отсутствие у предметов некоторых свойств. Например, "Иванов - спортсмен", "Все сладкоежки любят конфеты", "Ни один студент нашей группы не знает испанский язык", "Некоторые океаны имеют пресную воду".
Все атрибутивные суждения можно разделить на следующие типы: "a есть P", "Все S есть P", "Ни один S не есть P", "Некоторые S есть P", "Некоторые S не есть P". Эти суждения следующим образом переводятся на язык логики предикатов:
"a есть P" – P(a);
"Все S есть P" – "x(S(x) É P(x));
"Ни один S не есть P" – "x(S(x) É ØP(x));
"Некоторые S есть P" – $x(S(x) & P(x));
"Некоторые S не есть P" – $x(A(x) & ØP(x)).
Полезно понять и запомнить следующее правило: если кванторная переменная связана квантором общности ("), то в формуле используется знак импликации ( É), а если кванторная переменная связана квантором существования ($), то в формуле используется знак конъюнкции (&).
Пример 2.17.
Перевести на язык логики предикатов следующие суждения:
а) Веста – собака.
Заменим имя "Веста" символом "в" и введем предикат P(x) = "x – собака".
Наше суждение можно выразить формулой: P(в).
б) Всякая логическая функция может быть задана таблицей.
Введем предикаты S(x) = "x – логическая функция"; P(x) = "x может быть задана таблицей".
Наше суждение можно выразить формулой: "x(S(x) É P(x)).
в) Ни один народ не хочет войны.
Введем предикаты S(x) = "x – народ"; P(x) = "x хочет войны".
Наше суждение можно выразить формулой: "x(S(x) É ØP(x)).
г) Некоторые журналисты были в космосе.
Введем предикаты S(x) = "x – журналист"; P(x) = "x был в космосе".
Наше суждение можно выразить формулой: $x(S(x) & P(x)).
д) Некоторые современники динозавров не вымерли.
Введем предикаты S(x) = "x – современник динозавров"; P(x) = "x вымер".
Наше суждение можно выразить формулой: $x(A(x) & ØP(x)).
Суждения об отношениях выражают отношения между двумя, тремя и т. д. объектами. При переводе этих суждений в формулы используют многоместные предикаты и правила, рассмотренные выше. При переводе отрицаний суждений на язык формул применяется правило переноса квантора через знак отрицания и другие равносильные преобразования.
Пример 2.18.
Суждение “Некоторые студенты сдали все экзамены” записать в виде формулы логики предикатов. Построить отрицание данного суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Введем предикаты: A(x) = “x – студент”; B(y) = “y – экзамен”, C(x, y) = ”x сдал экзамен y”. Тогда предложение “Некоторые студенты сдали все экзамены” можно записать в виде следующей формулы:
$x (A(x)& "y (B(y) É C(x, y))).
Построим отрицание этой формулы, применяя равносильные преобразования:
Ø$x (A(x)& "y (B(y) É C(x, y))) º "x (ØA(x) Ú $y Ø(B(y) É C(x, y)) º "x (A(x) É $y (B(y)& ØC(x, y))).
Это предложение можно прочитать следующим образом:
“Каждый студент не сдал хотя бы один экзамен”.
Язык логики предикатов удобен для записи математических предложений: определений, теорем, необходимых и достаточных условий (см., например [5]).
Пример 2.19.
Записать на языке логики предикатов следующее определение предела числовой последовательности: "Число a является пределом числовой последовательности {an}, если для любого положительного числа e существует такой номер n0, что для всех натуральных чисел n, больших или равных n0, справедливо неравенство: |an - a| < e".
Введем предикаты: P(e) = "e > 0"; Q(n) = "n – натуральное число"; R(n, n0) = "n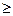 
n0"; S(n, e) = "|an - a| < e".
Определение предела последовательности может быть записано следующей формулой:
"e$n0"n(P(e)&Q(n)&Q(n0)&R(n, n0) É S(n, e)).
Пример 2.20.
Записать в виде формулы логики предикатов великую теорему Ферма (была доказана в 1996 г. Э. Вайлсом (Andrew Wiles)): "Для любого целого n > 2 не существует натуральных чисел x, y, z, удовлетворяющих равенству: xn + yn = zn".
Введем предикаты: N(x) = "x – натуральное число"; M(x) = "x > 2"; P(x, y, z, n) = "xn + yn = zn".
Для любых чисел x, y, z, n условие (посылка) теоремы Ферма есть конъюнкция N(x)&N(y)&N(z)&N(n)&M(n), а заключение есть ØP(x, y, z, n). Поэтому теорема Ферма формулируется следующим образом:
"x"y"z"n(N(x)&N(y)&N(z)&N(n)&M(n) É ØP(x, y, z, n)).
Если теорема имеет вид "x(P(x) É Q(x)), то предикат Q(x) является следствием предиката P(x). При этом предикат Q(x) называется необходимым условием предиката P(x), а предикат P(x) – достаточным условием предиката Q(x).
Пример 2.21.
Запишем в виде формулы логики предикатов утверждение: "Если число делится на 6, то оно делится на 3".
Введем предикаты P(x) = "x делится на 6"; Q(x) = "x делится на 3". Наше утверждение формулируется следующим образом: "x(P(x) É Q(x)).
Предикат P(x) (делимость на 6) является достаточным условием предиката Q(x) (делимость на 3). Предикат Q(x) (делимость на 3) является необходимым условием предиката P(x) (делимость на 6).