Основные характеристики нечетких множеств.

Нечеткие множества.

Нечеткое мн. – это такое мн., элементы которого входят в данное мн. с той или иной степенью вероятности. Пусть X – мн. принадлежащее E – универсальное мн. R – некоторое свойство. Обычное четкое подмножество А – универсального подмножества Е, элементы которого удовлетворяют свойству R, определяется как множество упорядоченных пар.

А = {μ_А(Х) / Х}

μ_А(Х) – характеристическая функция и для четкого подмножества А принимает значение 1, если Х удовлетворяет свойству R и 0 в ином случае.

Нечеткое подмножество отличается от обычного тем, что для Х (принадлежащего Е) нет однозначного ответа «да» или «нет» относительно свойства R. В связи с этим нечеткое подмножество A определяется таким же образом как и для четкого множества, но функция μ_А(Х) в этом выражении будет называться характеристической, которая принимает значения от 0 до 1. Множество М называется множеством принадлежностей. Функция принадлежности указывает степень принадлежности Х к множеству А. Если M = {0, 1}, то такое множество может рассматриваться как обычное четкое.

Ex Примеры записи нечетких множеств:

1. E={x₁,x₂,x₃,x₄,x₅} М=[0..1]

μ_А(x₁)=0.5 μ_А(x₂)=0.3 μ_А(x₃)=1 μ_А(x₄)=0 μ_А(x₅)=0.1

2. A={0.5/ x₁,0.3/x₂,1/x₃,0/x₄,0.1/x₅}

3. A={0.5/ x₁+0.3/x₂+1/x₃+0/x₄+0.1/x₅} неарифметическое сложение

Основные характеристики нечетких множеств.

Нечеткое множество – это такое множество, элементы которого входят в данное множество с той или иной степенью вероятности.

Пусть M = [0,1] и A - нечеткое множество с элементами из универсального множества E и множеством принадлежностей M.

Носителем (суппортом) нечёткого множества supp A называется множество

Эта величина называется высотой нечёткого множества A. Нечёткое множество A нормально, если его высота равна 1. Если высота строго меньше 1, нечёткое множество называется субнормальным.

Нечёткое множество пусто, если .

Непустое субнормальное нечёткое множество можно нормализовать по формуле:

Немодальное нечеткое мн. – такое мн., для которого , только для одного эл. x из универсального множества E.

Носитель нечеткого множества – обычное четкое подмножество, для которого выполняется μ_А(Х)>0.

Точки перехода нечеткого множества – такие элементы универсального множества E, для которых μ_А(Х)=0,5.

Ex Примеры нечетких множеств:

1. E={0,1,2,3,4,5,6}

“несколько”={0/0+0.3/1+0.9/2+1/.+0.7/4+0.3/5+0/6}

характеристиками являются: sup μ_А(Х) = 1

носителями являются: 1,2,3,4,5

точка перехода: -

2. E={0,1..∞} М=[0..1] Задание с пом ф-ии:

“мало”={ μ_А(Х) = 1/(1+(n/10)²)}

3. E={0,1..100} Задание с пом систем:

μ_{молодой}(Х)=

Логические операции над нечеткими множествами.

При М=[0,1]. Пусть A и B - нечеткие множества на универсальном множестве E.

Включение AcB

A содержится в B, если для любых x принадлежащих E выполняется:

μ_А(x) ≤ μ_B(x).

2. Равенство A=B

A и B равны, если для любых x принадлежащих E выполняется:

μ_А(x) = μ_B(x).

3. Дополнение A=B

A и B дополняют друг друга, если для любых x принадлежащих E выполняется: μ_А(x) = 1- μ_B(x).

В данном случае определено для М=[0,1], но можно и на любом другом диапазоне упорядоченных значений М.

4. Пересечение A∩B

5. Объединение AUB

6. Разность A-B= A∩B μ_A-B= min(μ_A(x) 1 - μ_B(x))

7. Дизъюнктивная сумма

μ_A(+)B= max{[min{ μ_A(x), 1 - μ_B(x)}, min{1 - μ_A(x), μ_B(x) }] }

Рассмотрим прямоугольную систему координат, по оси у – значения характеристической функции μ_А(x), а по оси х – в произвольном порядке расположены эл-ты унив. мн. Е.

Свойства:

Коммутативность

Ассоциативность

,

Идемпотентности

Дистрибутивность

,

5.

Закон Де Моргана

,

7.

Ассоциативность

3. з-н де Моргана

4. Идемпотентность

Дистрибутивность

6.

Свойства совместного использования:

1.

2.

Нечеткие отношения.

Обычным отношением R на множестве Х называется некоторое подмножество декартового произведения X*Y. Отсюда следует, что задать отношение R на множестве X, это задать все пары (х,у), которые связаны отношением R: x R y, (x,y) R

Если множество Х, на котором задано отношение R – конечно, то отношение может быть задано в двух формах:

1. в виде матрицы

||rij|| i=1..n, j=1..n

2. в виде графа

Отображение одного н/м в другое – нечеткая импликация (нечеткое отношение).

Операция нечеткой импликации может задаваться как припомощи соответствующей функции принадлежности, так и при помощи матрицы отношений, которая отображает одно н/м в другое.

1. В виде таблицы:

x=[x1,x2,x3] y=[y1,y2]

	y1	y2
x1	0.1	0.2
x2	0.3	0.4
x3	0.1

2. В виде функциональной зависимости:

Если х и у множеству всех действит чисел, зададим x>>y

3. В виде графической формы:

Четкое отношение (≥, x≥y)

Нечеткое отношение (>>,x>>y)

Нечетким отношением R называется нечеткое множество, определенное на декартовом произведении XхY, которому

соответствует функция принадлежности . отражает силу зависимости между и .

Нисходящие нечеткие выводы.

Рассмотренные до сих пор нечеткие выводы представляют собой восходящие выводы от предпосылок к заключению. В последние годы в динамических нечетких системах начинают применяться нисходящие нечеткие выводы.

Пример: возьмем упрощенную модель диагностики неисправности автомобиля с именами переменных Х=[ Х1, Х2, Х3] У=[ У1, У2 ]:

Х1- обработка машинного масла

Х2 – затруднение при запуске

У1 – ухудшение цвета выхлопных газов

У2 – недостаток мощности.

Между переменными Хi и Yi существуют нечеткие причинные отношения, которые можно представить в виде некоторой матрицы с элементами R_ij принадлежащими [0;1]. Конкретные предпосылки и заключения можно рассмотреть как нечеткие множества Х и У. Отношения этих множеств можно обозначить следующим образом:

У=X◦R

В данном случае направление выводов является обратным направлением вывода. выходы В (симптомы) определяют входы А(факторы).

Матрица R- знания эксперта:

	y1	y2
x1	0.9	0.6
x2	0.1	0.5
x3	0.2	0.5

Результат осмотра: Х= 0,9/х1+0,1/х2+0,2/х3=[0.9;0.1;0.2]

У=X◦R = 0.9/y1+0.6/y2.

Т.е. можно сделать вывод, что, скорее всего, неисправен аккумулятор.

На практике в подобных задачах могут одновременно использоваться различные композиции нечетких выводов. Сама схема выводов может быть многокаскадной. Общих методов решения подобных задач не существует. Операции суммирования и умножения заменяются на операции объединения и пересечения.

Байесовские сети доверия.

Байесовская сеть (или Байесовская сеть доверия) — это вероятностная модель, представляющая собой множество переменных и их вероятностных зависимостей. Например, байесовская сеть может быть использована для вычисления вероятности того, чем болен пациент по наличию или отсутствию ряда симптомов, основываясь на данных о зависимости между симптомами и болезнями.

Формально, байесовская сеть — это направленный ациклический граф, вершины которого представляют переменные, а ребра кодируют условные зависимости между переменными. Вершины могут представлять переменные любых типов, быть взвешенными параметрами, скрытыми переменными или гипотезами.

Если ребро выходит из вершины A в вершину B, то A называют предком B, а B называют сыном A. Множество вершин-предков вершины X_i обозначим как parents(X_i). Совместное распределение значений в вершинах можно удобно расписать как результат локальных распределений в каждом узле и его предках:

Если у вершины X_i нет предков, то его локальное распределение вероятностей называют безусловным, иначе условным. Если значение в узле получено в результате опыта, то вершину называют свидетелем.

Граф кодирует зависимости между переменными. Условная независимость представлена графическим свойством d-разделенности.

Два узла направленного графа x и y называются d-разделенными, если для всякого пути из x в y (здесь не учитывается направление ребер) существует такой промежуточный узел z (не совпадающий ни с x, ни с y), что либо связь в пути в этом узле последовательная или расходящаяся, и узел z получил означивание, либо связь сходящаяся, и ни узел z, ни какой-либо из его потомков означивания не получил. В противном случае узлы называются d-связанными.Свидетельства — утверждения вида «событие в узле x произошло». Например: «Компьютер не загружается».

Процесс рассуждения в байесовских сетях доверия. Пример построения простейшей байесовской сети доверия.

Вероятности события в ЭС распространяются в БЗ на основе правила Байесса.

Рассматриваем небольшую яблочную плантацию «яблочного Джека». Однажды Джек обнаружил, что его прекрасное яблочное дерево лишилось листвы. Теперь он хочет выяснить, почему это случилось. Он знает, что листва часто опадает, если:

дерево засыхает в результате недостатка влаги; или дерево болеет.

Данная ситуация может быть смоделирована байесовской сетью доверия, содержащей 3 вершины: «Болеет», «Засохло» и «Облетело».

Рис.1. Пример байесовской сети доверия с тремя событиями.

В данном простейшем случае рассмотрим ситуацию, при которой каждая вершина может принимать всего лишь два возможных состояний и, как следствие находится в одном из них, а именно:

Вершина (событие) БСД Состояние 1 Состояние 2

“Болеет” «болеет» «нет»

“Засохло” «засохло» «нет»

“Облетело” «да» «нет»

Вершина “Болеет” говорит о том, что дерево заболело, будучи в состоянии «болеет», в противном случае она находится в состоянии «нет». Аналогично для других двух вершин. Рассматриваемая байесовская сеть доверия, моделирует тот факт, что имеется причинно-следственная зависимость от события “Болеет” к событию “Облетело” и от события “Засохло” к событию “Облетело”. Это отображено стрелками на байесовской сети доверия.Когда есть причинно-следственная зависимость от вершины А к другой вершине B, то мы ожидаем, что когда A находится в некотором определённом состоянии, это оказывает влияние на состояние B. Следует быть внимательным, когда моделируется зависимость в байесовских сетях доверия. Иногда совсем не очевидно, какое направление должна иметь стрелка.

Например, в рассматриваемом примере, мы говорим, что имеется зависимость от “Болеет” к “Облетело”, так как когда дерево болеет, это может вызывать опадание его листвы. Опадание листвы является следствием болезни, а не болезнь – следствием опадания листвы.На приведенном выше рисунке дано графическое представление байесовской сети доверия. Однако, это только качественное представление байесовской сети доверия. Перед тем, как назвать это полностью байесовской сетью доверия необходимо определить количественное представление, то есть множество таблиц условных вероятностей:

Априорная вероятность p(“Болеет”)

Априорная вероятность p(“Засохло”)

Болеет = «болеет» Болеет = «нет»

Засохло = «засохло» Засохло = «нет»

0,1 0,9

0,1 0,9

Таблица условных вероятностей p(“Облетело” | ”Болеет”, ”Засохло”)

Засохло = «засохло» Засохло = «нет»

Болеет = «болеет» Болеет = «нет» Болеет = «болеет» Болеет = «нет»

Облетело = «да» 0,95 0,85 0,90 0,02

Облетело = «нет» 0,05 0,15 0,10 0,98

Приведенные таблицы иллюстрируют ТУВ для трёх вершин байесовской сети доверия. Заметим, что все три таблицы показывают вероятность пребывания некоторой вершины в определённом состоянии, обусловленным состоянием её родительских вершин. Но так как вершины Болеет и Засохло не имеют родительских вершин, то их вероятности являются маргинальными, т.е. не зависят (не обусловлены) ни от чего.

На данном примере мы рассмотрели, что и как описывается очень простой байесовской сетью доверия. Современные программные средства (такие как MSBN, Hugin и др.) обеспечивают инструментарий для построения таких сетей, а также возможность использования байесовских сетей доверия для введения новых свидетельств и получения решения (вывода) за счёт пересчёта новых вероятностей во всех вершинах, соответствующих вновь введенным свидетельствам.

В нашем примере пусть известно, что дерево сбросило листву. Это свидетельство вводится выбором состояния «да» в вершине “Облетело”. После этого можно узнать вероятности того, что дерево засохло. Для приведенных выше исходных данных, результаты вывода путем распространения вероятностей по БСД будут:

p( “Болеет” = «болеет» | “Облетело” = «да») = 0,47; p( “Засохло” = «засохло» | “Облетело” = «да») = 0,49.

Генетический алгоритм.

Генетический алгоритм (ГА) представляет собой метод оптимизации, основанный на концепциях естественного отбора и генетики. В этом подходе переменные, характеризующие решение, представлены в виде ген в хромосоме. ГА оперирует конечным множеством решений (популяцией) - генерирует новые решения как различные комбинации частей решений популяции, используя такие операторы, как отбор, рекомбинация (кроссинговер) и мутация. Новые решения позиционируются в популяции в соответствии с их положением на поверхности исследуемой функции.

Для реализации этого используют моделирование эволюции (естественного отбора) или если проще - борьбы за выживание. В природе, по упрощенной схеме, каждое животное стремится выжить, чтобы оставить после себя как можно больше потомства. Выжить в таких условиях могут лишь сильнейшие.

Тогда нам остается организовать некоторую среду - популяцию, населить её решениями - особями, и устроить им борьбу. Для этого нужно определить функцию, по которой будет определяться сила особи - качество предложенного ею решения. Основываясь на этом параметре можно определить каждой особи количество оставляемых ею потомков, или вероятность того, что эта особь оставит потомка. Причем, не исключен вариант, когда особь со слишком низким значением этого параметра умрёт.

Допустим нам нужно оптимизировать некоторую функцию F(X1,X2,..,Xn). Пусть мы ищем её глобальный максимум. Тогда, для реализации ГА нам нужно придумать, как мы будем хранить решения. По сути, нам нужно поместить все X1-Xn в некоторый вектор, который будет играть роль хромосомы. Один из наиболее распространенных способов - кодировать значения переменных в битовом векторе. Например, выделим каждому иксу по 8 бит. Тогда наш вектор будет длины L=8*n. Для простоты будем считать, что биты лежат в массиве X[0..L-1].

Пусть каждая особь состоит из массива X и значения функции F на переменных, извлеченных из этого массива.

Тогда ГА будет состоять из следующих шагов:

1.Генерация начальной популяции - заполнение популяции особями, в которых элементы массива X (биты) заполнены случайным образом.

2.Выбор родительской пары - берем K особей с максимальными значениями функции F и составляю из них все возможные пары (K*(K-1)/2). Репродукция - процесс, в котором хромосомы копируются согласно их целевой функции

3.Кроссинговер - берем случайную точку t на массиве X (0..L-1).

Теперь, все элементы массива с индексами 0-t новой особи (потомка) заполняем элементами с теми же индексами, но из массива X первой родительской особи. Остальные элементы заполняются из массива второй родительской особи. Для второго потомка делается наоборот - элементы 0-t берут от второго потомка, а остальные - от первого.

4.Новые особи с некоторой вероятностью мутируют - инвертируется случайный бит массива X этой особи. Вероятность мутации обычно полагают порядка 1%.

5.Полученные особи-потомки добавляются в популяцию после переоценки. Обычно новую особь добавляют взамен самой плохой старой особи, при условии что значение функции на новой особи выше значения функции на старой - плохой особи.

6.Если самое лучшее решение в популяции нас не удовлетворяет, то переход на шаг 2. Хотя, чаще всего этого условия нет, а итерации ГА выполняются бесконечно.

Преимущества

Они не требуют никакой информации о поверхности ответа;

Разрывы, существующие на поверхности ответа имеют незначительный эффект на полную эффективность оптимизации;

Они стойки к попаданию в локальные оптимумы;

Они хорошо работают при решении крупномасштабных проблем оптимизации;

Могут быть использованы для широкого класса задач;

Просты и прозрачны в реализации;

Могут быть использованы в задачах с изменяющейся средой.

НедостаткиНе желательно и проблематично использовать ГА:

В случае когда необходимо найти точный глобальный оптимум;

Время исполнения функции оценки велико;

Необходимо найти все решения задачи, а не одно из них;

Конфигурация является не простой (кодирование решения).

Namemf(x, params),

гдеnamemf – наименование функции принадлежности;
x– вектор, для координат которого необходимо рассчитать значения функции принадлежности;
params– вектор параметров функции принадлежности.

Простейшие функции принадлежности треугольная (trimf) и трапециевидная (trapmf) формируется с использованием кусочно-линейной аппроксимации. Трапециевидная функция принадлежности является обобщение треугольной, она позволяет задавать ядро нечеткого множества в виде интервала. В случае трапециевидной функции принадлежности возможна следующая удобная интерпретация: ядро нечеткого множества – оптимистическая оценка; носитель нечеткого множества – пессимистическая оценка.

Две функции принадлежности – симметричная гауссовская (gaussmf) и двухстороняя гауссовская (gaussmf) формируется с использованием гауссовского распределения. Функция gaussmf позволяет задавать ассиметричные функция принадлежности. Обобщенная колоколообразная функция принадлежности (gbellmf) по своей форме похожа на гауссовские. Эти функции принадлежности часто используются в нечетких системах, так как на всей области определения они является гладкими и принимают ненулевые значения.

Функции принадлежности sigmf,dsigmf, psigmf основаны на использовании сигмоидной кривой. Эти функции позволяют формировать функции принадлежности, значения которых начиная с некоторого значения аргумента и до + (-) 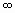равны 1. Такие функции удобны для задания лингвистических термов типа “высокий” или “низкий”.

Полиномиальная аппроксимация применяется при формировании функций zmf, pimf и smf, графические изображения которых похожи на функции sigmf,dsigmf, psigmf, соответственно.

Основная информация о встроенных функциях принадлежности сведена в табл. 6.1. На рис. 6.1 приведены графические изображения функций принадлежности, полученные с помощью демонстрационной сценария mfdemo. Как видно из рисунка, встроенные функции принадлежности позволяют задавать разнообразные нечеткие множества.

В Fuzzy Logic Toolbox предусмотрена возможность для пользователя создания собственной функции принадлежности. Для этого необходимо создать m-функцию, содержащую два входных аргумента – вектор, для координат которого необходимо рассчитать значения функции принадлежности и вектор параметров функции принадлежности. Выходным аргументом функции должен быть вектор степеней принадлежности. Ниже приведена m-функция, реализующая колоколообразную функцию принадлежности :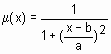

Область визуализации

В этой области выводится два типа информации:

· при обучении системы – кривая обучения в виде графика зависимости ошибки обучения от порядкового номера итерации.

· при загрузке данных и тестировании системы – экспериментальные данные и результаты моделирования.

Экспериментальные данные и результаты моделирования выводятся в виде множества точек в двумерном пространстве. При этом по оси абцисс откладывается порядковый номер строчки данных в выборке (обучающей, тестирующей или контрольной), а по оси ординат - значение выходной переменной для данной строчки выборки. Используются следующие маркеры:

голубая точка (.) – теструющая выборка;

голубая окружность (o) – обучающая выборка;

голубой плюс (+) – контрольная выборка;

красная звездочка (*) – результаты моделирования.

Область свойств ANFISВ области свойств ANFIS (ANFIS info) выводится информация о количестве входных и выходных переменных, о количестве функций принадлежностей для каждой входной переменной, а также о количестве строчек в выборках. В этой области расположены две кнопки Structureи Clear Plot.

Нажатие кнопки Structureоткрыет новое графическое окно, в котором система нечеткого логического вывода представляет в виде нейро-нечеткой сети.

Нажатие кнопки Clear Plotпозволяет очистить область визуализации.

Область загрузки данных

В области загрузки данных (Load data) расположены:

· меню выбора типа данных (Type), содержащее альтернативы:

o Traning -обучающая выборка;

o Testing - тестирующая выборка;

o Checking - контрольная выборка;

o Demo - демонстрационный пример;

· меню выбора источника данных (From), содержащее альтернативы:

o disk – диск;

o worksp.-рабочая область MatLab;

· кнопка загрузки данных Load Data…;

· кнопка очистки данных Clear Data.

Примечание. В течении одной сеанса работы ANFIS-редактора можно загружать данные одного формата, т.е. количество входных переменных в выборках должно быть одинаковым.

Область обучения

В области обучения (Train FIS) расположены меню выбора метода оптимизации (Optim. method), поле задания требуемой точности обучения (Error tolerance),поле задания количества итераций обучения (Epochs) и кнопка Train Now, нажатие которой запускает режим обучение. Промежуточные результаты обучения выводятся в область визуализации и в рабочую област MatLab. В ANFIS-редакторе реализованы два метода обучения:

· backpropa – метод обратного распространения ошибки, основанный на идеях метода наискорейшего спуска;

· hybrid –гибридный метод, объединяющий метод обратного распространения ошибки с методом наименьших квадратов.

Область тестирования

В области тестирования (Test FIS) расположены меню выбора выборки и кнопка Test Now, по нажатию по которой происходит тестирование нечеткой системы с выводом результатов в область визуализации.

Нечеткие множества.

Нечеткое мн. – это такое мн., элементы которого входят в данное мн. с той или иной степенью вероятности. Пусть X – мн. принадлежащее E – универсальное мн. R – некоторое свойство. Обычное четкое подмножество А – универсального подмножества Е, элементы которого удовлетворяют свойству R, определяется как множество упорядоченных пар.

А = {μ_А(Х) / Х}

μ_А(Х) – характеристическая функция и для четкого подмножества А принимает значение 1, если Х удовлетворяет свойству R и 0 в ином случае.

Нечеткое подмножество отличается от обычного тем, что для Х (принадлежащего Е) нет однозначного ответа «да» или «нет» относительно свойства R. В связи с этим нечеткое подмножество A определяется таким же образом как и для четкого множества, но функция μ_А(Х) в этом выражении будет называться характеристической, которая принимает значения от 0 до 1. Множество М называется множеством принадлежностей. Функция принадлежности указывает степень принадлежности Х к множеству А. Если M = {0, 1}, то такое множество может рассматриваться как обычное четкое.

Ex Примеры записи нечетких множеств:

1. E={x₁,x₂,x₃,x₄,x₅} М=[0..1]

μ_А(x₁)=0.5 μ_А(x₂)=0.3 μ_А(x₃)=1 μ_А(x₄)=0 μ_А(x₅)=0.1

2. A={0.5/ x₁,0.3/x₂,1/x₃,0/x₄,0.1/x₅}

3. A={0.5/ x₁+0.3/x₂+1/x₃+0/x₄+0.1/x₅} неарифметическое сложение

Основные характеристики нечетких множеств.

Нечеткое множество – это такое множество, элементы которого входят в данное множество с той или иной степенью вероятности.

Пусть M = [0,1] и A - нечеткое множество с элементами из универсального множества E и множеством принадлежностей M.

Носителем (суппортом) нечёткого множества supp A называется множество

Эта величина называется высотой нечёткого множества A. Нечёткое множество A нормально, если его высота равна 1. Если высота строго меньше 1, нечёткое множество называется субнормальным.

Нечёткое множество пусто, если .

Непустое субнормальное нечёткое множество можно нормализовать по формуле:

Немодальное нечеткое мн. – такое мн., для которого , только для одного эл. x из универсального множества E.

Носитель нечеткого множества – обычное четкое подмножество, для которого выполняется μ_А(Х)>0.

Точки перехода нечеткого множества – такие элементы универсального множества E, для которых μ_А(Х)=0,5.

Ex Примеры нечетких множеств:

1. E={0,1,2,3,4,5,6}

“несколько”={0/0+0.3/1+0.9/2+1/.+0.7/4+0.3/5+0/6}

характеристиками являются: sup μ_А(Х) = 1

носителями являются: 1,2,3,4,5

точка перехода: -

2. E={0,1..∞} М=[0..1] Задание с пом ф-ии:

“мало”={ μ_А(Х) = 1/(1+(n/10)²)}

3. E={0,1..100} Задание с пом систем:

μ_{молодой}(Х)=