Условные (импликативные) высказывания

Условными называются сложные высказывания, состоящие из двух частей, связанных между собой логическим союзом «если, то». Часть со словом «если» называется основанием, или антецедентом, а часть словом «то» — следствием, или консеквентом. В высказывании «Если человек болен, то он не может трудиться» первая часть «если человек болен» — основание, а вторая — «то он не может трудиться» — следствие.
В естественном языке союз «если, то» употребляется по меньшей мере в четырех смыслах и, соответственно, выражает столько же различных логических союзов. Союз «если, то», во-первых, употребляется в смысле «если р, то обязательно q». «Если спираль перегорит, то электрический чайник выйдет из строя». ( Прямая импликация, или просто импликация)

Во-вторых, он может употребляться в смысле «если р, то, возможно, q», или « только если p, то q» — «Если мы будем в Париже, то посетим Лувр» (обратная импликация, или репликация). В-третьих, союз «если, то» употребляется в смысле «если и только если р, то
q», или «p тогда и только тогда, когда q» — «Если треугольник равносторонний, то он — равноугольный» (двойная импликация, или эквиваленция). В-четвертых, союз «если, то» может употребляться в смысле соединительного союза «а». «Если вчера стояла хорошая погода, то сегодня идет дождь».

На приведенных выше примерах рассмотрим, как зависит
логическое значение сложного высказывания от логического
значения его составных частей.

Первый пример может описывать следующие ситуации:

а) спираль перегорела, и электрический чайник вышел из строя;

б) спираль перегорела, но электрический чайник не вышел из строя;

в) спираль не перегорела, но электрический чайник вышел из строя;

г) спираль не перегорела, и электрический чайник не вышел из строя.

Нетрудно заметить, что невозможной является только вторая
ситуация.

Таким образом, импликация ложна только тогда, когда основание истинно, а следствие ложно. Из ситуаций, которые могут быть описаны вторым примером, невозможной является третья, т.е. невозможно посетить Лувр, не побывав в Париже. Таким образом, репликация ложна только тогда, когда основание ложно, а следствие истинно.

Из содержания третьего примера следует, что невозможно, чтобы треугольник был равносторонним, но не был равноугольным, или был равноугольным, но не был равносторонним. Поэтому эквиваленция истинна только тогда, когда обе ее части либо истинны, либо ложны. Приведем сводную таблицу связи суждений с помощью этих логических союзов.

P	Q	P → Q (импликация)	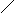P Q ( реимпликация)	P ↔ Q (эквиваленция)
И	И	И	И	И
И	Л	Л	И	Л
Л	И	И	Л	Л
Л	Л	И	И	И

СВОДНАЯ ТАБЛИЦА ВОЗМОЖНЫХ СВЯЗЕЙ МЕЖДУ ВЫСКАЗЫВАНИЯМИ

В логике принято характеризовать логические союзы таким способом, при котором логическое значение сложного высказывания ставится в зависимость от логических значений входящих в его состав простых. Приведем таблицу соответствующих языковых эквивалентов логических связей.

Варианты значений	Выражения логической связи через известные союзы	Возможные соответствия в естественном языке
p	и	и	л	л
q	и	л	и	л
p R1 q	и	и	и	и	p v p ^ q v q	Закон исключенного третьего
p R2 q	и	и	и	л	p v q	Слабая дизъюнкция
p R3 q	и	и	л	и	p q	Репликация ( обратная импликация)
p R4 q	и	л	и	и	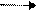p q	Импликация
p R5 q	л	и	и	и	p v q	Или не-p, или не-q
p R6 q	и	и	л	л	(q v q) ^ p	Независимо от того, q или не-q , но p
p R7 q	и	л	л	и	p ↔ q	Эквиваленция
p R8 q	л	л	и	и	(q v q) ^ p	Независимо от того, q или не-q , но не -p
p R9 q	л	и	и	л	p V q	Строгая дизъюнкция
p R10 q	и	л	и	л	(p v p) ^ q	Независимо от того, p или не-p , но q
p R11 q	л	и	л	и	(p v p) ^ q	Независимо от того, p или не-p , но не -q
p R12 q	и	л	л	л	p ^ q	Конъюнкция
p R13 q	л	и	л	л	p ^ q	Хотя и p, но не-q
p R14 q	л	л	и	л	p ^ q	Хотя и не- p, но q
p R15 q	л	л	л	и	p ^ q	Ни p, ни q
p R16 q	л	л	л	л	( p ^ p) v ( q ^ q )	Логическое противоречие