Составленные высказывания (логические функции)
Из простых высказываний с помощью связок И, ИЛИ и НЕ образовываются составные высказывания, которые называют логическими функциями. Простые высказывания, из которых образовывается составленное, называются логическими аргументами. Предложение «Больной ощущает сильную боль в области челюсти, рот самостоятельно не закрывается, тяжело глотать и говорить» является составленным высказыванием (логической функцией «И»).
Проблемное, достоверное, условное высказывание
Высказывание по своему смыслу может быть проблемным, достоверным или условным
Проблемное – это высказывание, в котором что-то утверждается или отрицается с определенной степенью предположения. Например, “причиной головной боли является, наверное, повышенное давление”.
Достоверное – это высказывание, которые содержит знание, обоснованные и проверенные практикой. Например, “человек дышит воздухом”.
Условное – это высказывание, в котором отображается зависимость того или иного явления от тех или других обстоятельств и в котором основание и следствие соединяются с помощью логического союза “если … , это ... ” Например, “если диагноз инфаркт миокарда, то наблюдается нарушение сердечного ритма». Таким образом, в условном высказывании нужно различать основание и следствие.
Множество значений высказывания
Любое высказывание может соответствовать или не соответствовать действительности. В первом случае оно называется истинным, во втором - ложным. Истинное высказывание можно обозначать символом 1, а ошибочное + символом 0 или наоборот. Такое обозначение является условным. Можно также использовать другие символы-обозначения: истинное высказывание обозначить символом И, а ложное Л. Таким образом, не считаясь с разнообразие высказываний, все они в алгебре логики могут приобретать только два значений: 1 или 0.
Существуют высказывания, которые всегда истинны. Например, «Человек дышит воздухом», «Пневмония – воспаление легких». Обозначив приведенные высказывания через X и Y соответственно, можно записать
Х = 1, Y=1.
Существуют высказывания ошибочные. Например, «Анемия – это сердечная недостаточность», «Для развития живого организма нужен никотин». Обозначив их через S и P соответственно, можем записать
S = 0, P=0.
Большинство высказываний могут быть истинными или ошибочными. Высказывание «кожа человека бледно-розового цвета» верно лишь для здорового человека, в других случаях - импликация; «
Логические операции и таблицы истинности.
Бинарные и унарные операторы.
Логика оперирует конечным числом операторов. Множество логических операторов разделяют на две группы:
Бинарные операторы используют две логические переменные. Сюда принадлежат операторы «И», «ИЛИ».
Унарные операторы используют одну логическую переменную. Эту группу образует оператор возражения «НЕ» и другие побитовые операции.
Операция возражения.
Договоримся обозначать простые высказывания буквами латинского алфавита: А, В, С... Значение истинности будем сокращенно обозначать цифрой 1 для «ИСТИНА» и 0 для «ЛОЖЬ».
Рассмотрение логических операций начнем с простейшей - операции возражения, которой в обычном языке соответствует частица «не». Эту операцию обозначают знаком Ø (иногда высказывание ØА обозначают также 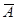 ). Высказывание ØА читается так: «не А».
). Высказывание ØА читается так: «не А».
Если А - некоторое высказывание, например, «у пациента выявлена пневмония», то ØА - новое составленное высказывание «у пациента не выявлена пневмония». Легко видеть, что если А - истинное высказывание, то ØА - ошибочное и наоборот. Этот факт положен в основу определения логической операции «Ø»:
Высказывания называется возражением высказывания А, если оно истинное, когда А – ошибочное и ошибочное, когда А – истинное. Действие операции представим в виде таблицы (или матрицы) истинности для отрицания
Таблица 9.1. Таблица истинности для возражения
| A | ØА |
Операция конъюнкции
Следующая логическая операция - конъюнкция, отвечает в обычном языке союзу «и». Обозначается конъюнкция символом «^», который относится между высказываниями. Если А и В - высказывание, то А ^ В – составленное высказывание (читается «А и В»).
Пусть А высказывание: «У больного повышенная температура», а В «У больного повышенное давление». Тогда А ^ В будет высказывание «У больного повышенная температура и повышено давление». Образованное высказывание истинное только тогда, когда истинны оба высказывания, которые входят в него. Т.е., операция конъюнкции определяется таким образом:
Конъюнкцией высказываний А и В называется такое высказывание, которое истинное тогда и только тогда, когда истине высказывания А и В. Таблица истинности конъюнкции представлена ниже.
Приведенная таблица является таблицей умножения двух чисел 0 и 1. Поэтому конъюнкцию называют еще логическим умножением и записывают: А Ù В = А × В.
Таблица истинности для конъюнкции
| A | B | A Ù B |
| A | B | A Ú B |
