РАЗРЕШЕНИЯ ПРОБЛЕМА, или: Разрешимости проблема

— проблема нахождения для данной дедуктивной теории общего метода, позволяющего решать, может ли отдельное утверждение, сформулированное в терминах теории, быть доказано в ней или нет. Этот общий метод, являющийся эффективной процедурой (алгоритмом), называется процедурой разрешения или разрешающей процедурой, а теория, для которой такая процедура существует, — разрешимой теорией.

Р. п. решается в классической логике высказываний с помощью таблиц истинности. Разрешающий алгоритм существует и для логики одноместных предикатов, для силлогизма категорического и других простых дедуктивных теорий. Но уже для логики предикатов общего решения Р. п. не существует. В математике также невозможно установить общий метод, который дал бы возможность провести различие между утверждениями, которые могут быть доказаны в ней, и теми, которые в ней недоказуемы.

Невозможность найти для теории общий разрешающий метод не исключает поиска процедуры разрешения для отдельных классов ее утверждений.

РАЗРЕШИМАЯ ТЕОРИЯ

— теория, для которой существует эффективная процедура (алгоритм), позволяющая о каждом утверждении, сформулированном в терминах этой теории, решить, выводимо оно в теории или нет (см.: Разрешения проблема).

Р. т. являются, напр., элементарная алгебра Буля, теория сложения целых чисел и некоторые иные простые математические теории. Неразрешима арифметика целых чисел (т. е. теория четырех главных арифметических действий над целыми числами) и каждая дедуктивная теория, содержащая арифметику.

РАЦИОНАЛЬНОСТЬ (от лат. ratio - разум)

- относящееся к разуму, обоснованность разумом, доступное разумному пониманию, в противоположность иррациональности как чему-то неразумному, недоступному разумному пониманию.

В методологии научного познания Р. понимается двояко. Чаще всего Р. истолковывается как соответствие законам разума — законам логики, методологическим нормам и правилам. То, что соответствует логико-методологическим стандартам, — Р., то, что нарушает эти стандарты, — нерационально или даже иррационально. Иногда под Р. понимают целесообразность. То, что способствует достижению цели, — Р., то, что этому препятствует, — нерациональность.

До недавних пор считалось, что образцом Р. деятельности является наука и деятельность ученого. Все остальные сферы человеческой деятельности Р. лишь в той мере, в какой они опираются на научные знания и методы. В настоящее время признано, что каждая область деятельности имеет свои стандарты Р., которые далеко не всегда совпадают с научными, поэтому можно говорить о Р. в искусстве, в политике, в управлении и т. д. Поэзия столь же Р., как и наука, но в ней иные стандарты Р.

РЕКУРСИВНОЕ ОПРЕДЕЛЕНИЕ (от лат. recurso - возвращаюсь)

— метод определения арифметической функции φ(у) или предиката Р(у) через область значений этой функции или предиката. Примером Р. о. может быть определение функции сложения:

а + 0 = а, (1)

а + b '=(а+ b)' (2)

В равенстве (1) говорится, что некоторое фиксированное число а (см.: Параметр) при прибавлении к нему нуля дает число а. В равенстве (2) говорится., что если к некоторому фиксированному числу а добавить число, следующее за некоторым фиксированным числом b (т. е. b ', или число b+1), то эта сумма будет равна числу, следующему за суммой чисел а+ b. Напр., если к числу 2 добавить число, следующее за числом 3, т. е. число 4, то этот же результат можно получить, сложив 2 и 3 и перейдя от полученной суммы к следующему за ней числу. Значение левой и правой частей равенства в данном случае равно 6. Такого рода функции позволяют вычислять значение суммы самых различных чисел. При этом осуществляется переход от некоторого числа п к следующему за ним (к п', или п+1), т. е. строится натуральный ряд чисел начиная с нуля. Допустим, нам требуется сложить 5 и 2. Тогда число 2 представим как следующее за 1, т. е. как 1'. Итак, имеем:

а)5+2=5+1'=(5+1)' по равенству (2), б)5+1=5+0'=(5 + 0)' по равенству (2),

в) 5+0=5 - по равенству (1).

Теперь будем возвращаться от равенства 5+0=5 (в) к равенству (б), а затем к равенству (а). Раз 5+0=5, то (5+0)'=6 (см. равенство (б)). Раз 5+1 равно 6, то (5+1)'=7 (см. равенство (а)). Итак, 5+2=7. В основе вычислимости арифметических функций, определяемых рекурсивно, лежит класс некоторых других функций, считающихся заданными с самого начала, которые называются примитивно-рекурсивными.

РЕЛЕВАНТНАЯ ЛОГИКА

- одна из наиболее известных неклассических теорий логического следования. В названии «Р. л.» отражается стремление выделить и систематизировать только уместные(релевантные) принципы логики, исключив, в частности, парадоксы импликации, свойственные импликации материальной классической логики, строгой импликации и др. импликациям.

В Р. л. формальным аналогом условного высказывания является релевантная импликация, учитывающая содержательную связь, существующую между основанием (антецедентом) и следствием (консеквентом) такого высказывания. Выражение «Утверждение A релевантно имплицирует утверждение В» означает, что В содержится в A и информация, представляемая В, является частью информации A. В частности, A не может релевантно имплицировать В, если в В не входит хотя бы одно из тех утверждений, из которых слагается А.

В Р. л. не имеет места принцип, позволяющий из противоречия выводить какое угодно высказывание. Эта логика является, таким образом, одной из паранепротиворечивых логик, не отождествляющих противоречивость опирающихся на них теорий с их тривиальностью, т. е. с доказуемостью в них любого утверждения.

В Р. л. логически истинное высказывание невыводимо из произвольно взятого высказывания.

• РЕФЕРЕНТ (от лат. refero - называть, обозначать) — объект, обозначаемый некоторым именем, то же, что и денотат. Напр., Р. выражения «первый космонавт» будет Юрий Гагарин (см.: Имя, Денотат).
• РЕФЕРЕНЦИЯ — отношение между обозначаемым и обозначающим, между предметом и его именем. Отношение Р. изучается теорией референции — разделом логической семантики (см.: Имя, Денотат).

СВОЙСТВО

— характеристика, присущая вещам и явлениям, позволяющая отличать или отождествлять их. Каждому предмету присуще бесчисленное количество свойств, которые делятся на существенные и несущественные, необходимые и случайные, общие и специфические и т. д.

В логике С. называют то, что обозначается одноместным предикатом, напр.: «... есть человек», «... есть зеленый» и т. п. При постановке на пустое место имени к.-л. объекта мы получаем истинное или ложное высказывание: «Сократ есть человек», «Снег зеленый».

СВЯЗКА

— в традиционной логике элемент простого суждения, соединяющий субъект и предикат. В повседневном языке С. обычно выражается словами «есть», «суть», «является» и т. п., напр.: «Узбеки являются жителями Средней Азии». В обыденной речи С. часто опускается и приведенное выше предложение обычно выглядит так: «Узбеки живут в Средней Азии». Однако даже если С. не выражена каким-то специальным словом, она обязательно присутствуют в суждении. Напр., два понятия «город» и «населенный пункт» образуют суждение только после того, как их соединит С. «Город есть неселенный пункт». Поэтому схематическое представление простого суждения включает в себя три элемента — субъект, предикат и связку: «5 есть Р». С. может быть утвердительной или отрицательной («есть» или «не есть»). Именно этим определяется качество простого суждения.

В символической логике пропозициональными связками называют логические союзы (операторы), с помощью которых из простых высказываний получают сложные высказывания. К ним обычно относят отрицание, конъюнкцию, дизъюнкцию, импликацию и т. п. Условия истинности сложных высказываний, содержащих пропозициональные связки, формулируются посредством таблиц истинности. (См.: Суждение.)

СЕМАНТИКА ЛОГИЧЕСКАЯ

— раздел логики (металогики), исследующий отношение языковых выражений к обозначаемым объектам и выражаемому содержанию. Проблемы семантики обсуждались еще в античности, однако в качестве самостоятельной дисциплины она стала оформляться на рубеже XIX—XX вв. благодаря работам Ч. Пирса, Г. Фреге, Б. Рассела. Значительный вклад в разработку проблем С. л. внесли А. Тарский, Р. Карнап, У. Куайн, Дж. Кемени, К. И. Льюис, С. Крипке и др. В течение длительного времени С. л. ориентировалась преимущественно на анализ формализованных языков, однако в последние 20 лет все больше исследований посвящается естественному языку.

В С. л. традиционно выделяют две области — теорию референции (обозначения) и теорию смысла. Теория референции исследует отношение языковых выражений к обозначаемым объектам, ее основными категориями являются: «имя», «обозначение», «выполнимость», «истинность», «интерпретация», «модель» и т. п. Теория референции служит основой теории доказательств в логике. Теория смысла пытается ответить на вопрос о том, что такое смысл языковых выражений, когда выражения являются тождественными по смыслу, как соотносятся смысл и денотат и т. п. Значительную роль в С.л. играет обсуждение семантических парадоксов, решение которых является важным критерием приемлемости любой семантической теории.

СЕМАНТИЧЕСКАЯ КАТЕГОРИЯ

-класс языковых выражений, взаимная замена которых в предложении сохраняет его грамматический статус, т. е. предложение остается предложением. Если, напр., в предложении «Волга впадает в Каспийское море» слово «Волга» мы заменим словом «Нева», то получим хотя и ложное, но все-таки предложение. Это означает, что слова «Волга» и «Нева» принадлежат одной С.к. Но если вместо слова «Волга» мы поставим слово «меньше», то у нас окажется бессмысленный набор слов, следовательно, слова «Волга» и «меньше» принадлежат разным С. к.

Наиболее известную систему С. к. разработал польский логик К. Айдукевич (1890—1963). Исходными категориями его системы являются категории собственных имен (n) и высказываний (s). Предполагается, что каждое правильно построенное выражение языка может быть расчленено на функтор и его аргументы. Категория функтора определяется как дробь, в знаменателе которой стоят категории аргументов, а в числителе - категория выражения, образующегося в результате сочленения функтора с аргументами.

Напр., к какой С. к. принадлежит одноместный предикат «...бел»? Его единственным аргументом является некоторое имя, категория которого помещается в знаменателе дроби; в результате соединения предиката с именем получается предложение, категория которого помещается в числителе дроби, получается 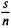. С. к. двухместного предиката, скажем, «больше», будет выглядеть так: 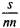. Логические связки можно рассматривать как функторы, применяемые к предложениям, причем в результате опять получается предложение. Т. о., категория бинарной связки, скажем, «или», «если, то» и т. п., будет выглядеть так: 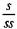. Теория С. к. служит основой для классификации формализованных языков и определения важных семантических понятий, например понятия истины.