Статистическое изучение динамики социально – экономических явлений.

Задача.Поданным ряда динамики об объёмах строительно– монтажных работ (СМР) (тыс руб.), выполненных строительными организациями за пятилетний период, вычислить:

1) абсолютные приросты (или снижения) – цепные и базисные;

2) темпы роста (или снижения) – цепные и базисные;

3) темпы прироста (или снижения) – цепные и базисные;

4) абсолютное содержание 1% прироста (или снижения). Полученные данные по пунктам 1- 4 представить в таблице.

5) среднегодовой объём работ;

6) средний абсолютный прирост.

7) среднегодовой темп роста и прироста (или снижения).

Построить график динамики объёмов строительных работ и сделать выводы.

Год	Объём работ (тыс.руб)	Абсолютный прирост (тыс.руб)	Темпы роста (%)	Темпы прироста(%)	Абс.сод.1% прироста (тыс.руб)
базисный	цепной	базисный	цепной	базисный	цепной
	87,5	-	-	-	-	-	-	-
	94,5	6,6	6,6	107,5	107,5	7,5	7,5	0,88
	91,5		-2,6	104,6	97,2	4,6	-2,8	-0,57
	97,8	10,3	6,3	111,8	106,9	11,8	6,9	0,53
		27,5	17,2	131,4	117,6	31,4	17,6	0,55
итого	485,9

1) Определяем базисный 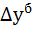и цепной 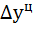абсолютные приросты по формулам:

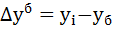
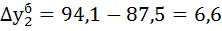
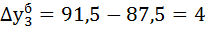
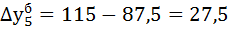
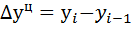
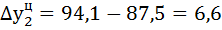
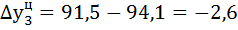
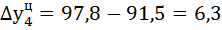
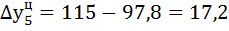
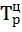2) Рассчитываем базисный и цепной темпы роста по формулам:

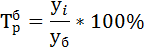
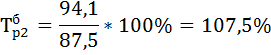
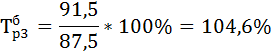
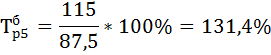
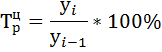
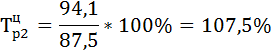
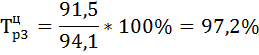
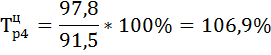
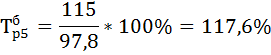
3) Определяем базисный и цепной темпы прироста по формулам:

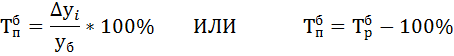
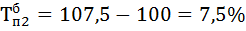
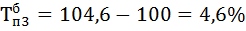
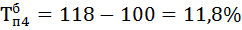
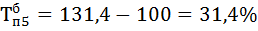
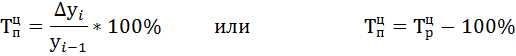
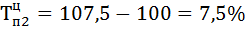
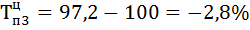
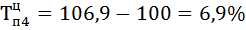
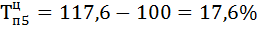
4) Находим абсолютное содержание одного процента прироста А% по формуле:

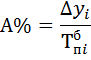
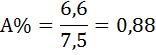
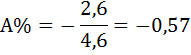
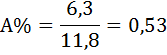
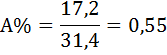
5) Вычисляем среднегодовой объем работ 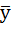по формуле:

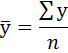
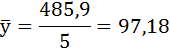
6) Рассчитываем средний абсолютный прирост 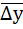по формуле:

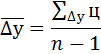
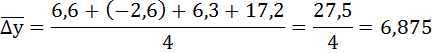
7) Находим средний темп роста 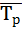по формуле:

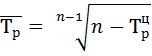
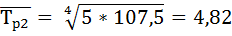
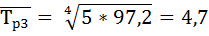
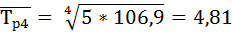
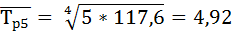
8) Определяем средний прирост 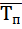по формуле:

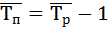
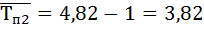
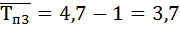
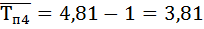
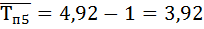
Вывод: В пятой год объем выполненных работ является наибольшим – 115 тыс. руб. , а так же темпа роста, прироста, абсолютного прироста самый высокий.

Объем выполненных работ в 3-ем году уменьшалось по сравнению с предыдущим 2 годом – 91,5 тыс. руб., а так же в этом году самые низкие темпы роста, прироста и абсолютного прироста.

Выборочный метод в статистических исследованиях. Показатели вариации.

Задача. Для изучения дневной выработки рабочих предприятия была проведена 10%- я бесповторная выборка, в результате которой получены исходные данные о распределении рабочих по производительности труда, представленные в таблице.

На основе приведенных данных вычислит:

1) среднедневную выработку рабочего;

2) дисперсию и среднеквадратическое отклонение;

3) коэффициент вариации;

4) предельную ошибку выборки;

5) границы среднедневной выработки генеральной совокупности. Сделать вывод.

Группа рабочих с дневной выработкой изделии,шт.		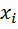Число рабочих,чел.	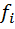	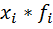x -	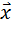(x -	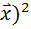(x -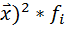
40-50				-22,9	524,41	3146,46
50-60				-12,9	166,41	2329,74
60-70				-2,9	8,41	294,35
70-80				7,1	50,41	1159,43
80-90				17,1	292,41	4386,15
итого						11316,13

1) Определяем среднедневную выработку рабочих 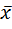по формулам:

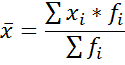
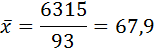
2) Вычисляем дисперсию по формулам:

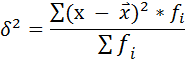
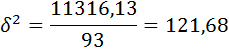
3) Рассчитываем среднеквадратическое отклонение по формуле:

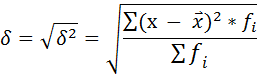
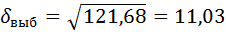
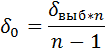
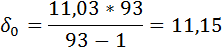
4) Находим коэффициент вариации по формуле:

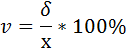
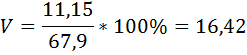
5) Определяем среднюю ошибку выборке 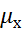по формуле:

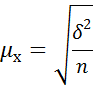
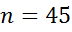
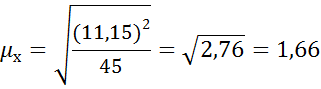
6) Определяем предельную ошибку выборки по формуле:

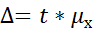
t=2

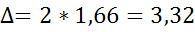
7) Находим границы среднедневной выработки генеральной совокупности по формуле:

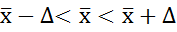
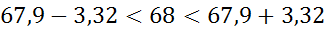
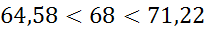
Вывод: Дневная выработка рабочего расположена в диапазоне от 64,58 до 71,22 изделий.

Аналитическое выравнивание.

Наименование
Среднемесячная номинальная начисленная з/п работников организаций, руб.	3521,3	5691,5	7295,6	8883,1			13227,9
Валовой региональный продукт, млн. руб	4372,3	44857,9		66476,2	82730,7	106441,5	108489,2