Задачи статистики в государственном и муниципальном управлении

Задачи статистики в государственном и муниципальном управлении

Основные задачи статистики в рыночной экономике

Статистика – одна из общественных наук, имеющая целью сбор, упорядочивание, анализ и сопоставление числового представления фактов, относящихся к самым разнообразным массовым явлениям. Целью данных действий является выявление каких-либо закономерностей, тенденций развития социально-экономических явлений и процессов.

Объектом изучения как науки является изучение количественные изменения массовых общественных явлений и процессов в неразрывной связи с их качественным содержанием.

Предметомвыступают размеры и количественные соотношения качественно определенных социально-экономических явлений, закономерности их связи и развития в конкретных условиях места и времени.

Задачи статистики определяются социально-экономическими потребностями общества.

Основные задачи статистики в рыночной экономике:

1) всестороннее исследование и освещение происходящих в обществе глубоких преобразований экономических и социальных про­цессов на основе научно обоснованной системы показателей;

2) обобщение и прогнозирование тенденций развития раз­личных отраслей экономики в целом;

3) выявление имеющихся резервов выхода из кризиса экономики;

4) своевременное обеспечение надежной информацией государственных, хозяйственных, экономических органов и широкой общественности.

Роль статистики в механизме управления экономикой

Статистика выполняет важную роль в механизме управления экономикой. Наличие систематической, полной и своевременной информации о происходящих процессах и явлениях – необходи­мое условие эффективных управленческих решений на государственном и региональном уровнях.

Расширенная коллегия Госкомстата России (24 декабря 1999 г.) определила следующие важнейшие задачи, стоящие пе­ред органами государственной статистики на 2000-2002 гг.:

1. Организация работ, связанных с подготовкой и проведе­нием Всероссийской переписи населения.

2. Приоритет вопросам совершенствования статистики малого предпринимательства (провести сплошные обследования малых предприятий по итогам их работы за 2000 г.).

3. Создание единого статистического информационного про­странства федеральных органов государственной власти и координация их статистической деятельности.

4. Целесообразность проведения переоценки основных фондов.

5. Совершенствование расчетов в области неформальной и скрытой экономики.

6. Повышение качества статистических разработок.

7. Совершенствование статистики отдельных отраслей соци­ально-экономической сферы.

8. Организация системы муниципальной статистики.

Использование статистических методов в процессе принятия решений

Под статистической методологией понимается система приемов, способов и методов, направленных на изучение количественных закономерностей, проявляющихся в структуре, динамике и взаимосвязях социально-экономических явлений.

Статистические методы используются комплексно (системно). Это обусловлено сложностью процесса экономико-статистического исследования, состоящего из 3х основных стадий:

1) сбор первичной статистической информации (стат. наблюдение);

2) статистическая сводка, обработка и группировка первичной информации;

3) обобщение, анализ и интерпретация статистической информации.

При изучении стат. информации широкое применение имеют табличный и графический методы.

Статистические распределения и их основные характеристики. Изучение корреляционной связи

Понятие ряда распределения. Атрибутивные и вариационные ряды распределения. Варианты, частоты и частности. Дискретные и непрерывные ряды. Построение дискретного и интервального вариационных рядов

После определения группировочного признака и границ групп строится ряд распределения.

Статистический ряд распределения представляет собой упо­рядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку. Он характе­ризует состав (структуру) изучаемого явления, позволяет судить об однородности совокупности, закономерности распределения и границах варьирования единиц совокупности.

Ряды распределения, построенные по атрибутивным призна­кам (в порядке возрастания или убывания наблюденных зна­ний), называются атрибутивными. Примером атрибутивных ря­дов могут служить распределения населения по полу, занятости, национальности, профессии и т.д.

Ряды распределения, построенные по количественному признаку, называются вариационными. Например, распределе­ние населения по возрасту, рабочих – по стажу работы, зара­ботной плате и т.д.

Вариационные ряды распределения состоят из двух элемен­тов: вариантов и частот.

Числовые значения количественного признака в вариацион­ном ряду распределения называются вариантами. Они могут быть положительными и отрицательными, абсолютными и от­носительными. Так, при группировке предприятий по результа­там хозяйственной деятельности варианты положительные (при­быль) и отрицательные (убыток) числа.

Частоты – это численности отдельных вариантов или каж­дой группы вариационного ряда, т. е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределе­ния. Сумма всех частот называется объемом совокупности и оп­ределяет число элементов всей совокупности.

Частности – это частоты, выраженные в виде относительных величин (долях единиц или процентах). Сумма частостей равна единице или 100%.

Вариационные ряды в зависимости от характера вариации под­разделяются на дискретные и интервальные. Дискретные вариаци­онные ряды основаны на дискретных (прерывных) признаках, имеющих только целые значения (например, тарифный разряд рабочих, число детей в семье); интервальные – на непрерывных при­знаках (имеющих любые значения, в том числе и дробные).

Способы построения дискретных и интервальных рядов различ­ны. Для построения дискретного ряда с небольшим числом вариантов выписываются все встречающиеся варианты значений признака, обозначаемые через x_i, а затем подсчитывается частота повторения каждого варианта f_i. Ряд распределения принято оформлять в виде таблицы, состоящей из двух колонок (или строк), в одной из кото­рых приводятся варианты, а в другой – частоты.

Для построения ряда распределения непрерывно изменяющихся признаков, либо дискретных, представленных в виде интервалов «от – до», необходимо установить оптимальное число групп (ин­тервалов), на которое следует разбить все единицы изучаемой со­вокупности. При группировке внутри однокачественной совокуп­ности появляется возможность применения равных интервалов, число которых зависит от вариации признака в совокупности и от количества обследованных единиц.

Основные типы корреляции

Прямые и обратные связи

В зависимости от направления действия функциональные и стохастические связи могут быть прямыми и обратными. При прямой связи направление измене­ния результативного признака совпадает с направлением изменения признака-фактора. В противном случае между рассматриваемыми величинами существуют обратные связи. Например, чем выше квалифика­ция рабочего (разряд), тем выше уровень производительности труда – прямая связь. А чем выше производительность труда, тем ниже себестоимость единицы продукции – обратная связь.

Прямолинейные и криволинейные связи. При прямолинейной связи с возрастанием значения факторного признака происходит непрерывное возрастание (или убывание) значений результативного признака. Математически такая связь представляется уравнением прямой, а графически — прямой линией. Отсюда ее более короткое название — линейная связь.

При криволинейных связях с возрастанием значения факторного признака возрастание (или убывание) результативного признака происходит неравномерно или же направление его изменения меняется на обратное. Геометрически такие связи представляются кривыми линиями (гиперболой, параболой и т.д.).

Однофакторные и многофакторные связи

По количеству факторов, действующих на результативный признак, связи различаются однофакторные (один фактор) и многофакторные (два и более факторов).

Понятие трудовых ресурсов

Трудовые ресурсы – это часть населения страны, которая фактически занята в экономике или же не занята, но способна к труду по возрасту и состоянию здоровья.

В состав трудовых ресурсов включают: 1) трудоспособное население в трудоспособном возрасте; 2) фактически работающих подростков моложе 16 лет; 3) фактически работающих лиц старше трудоспособного возраста.

Система национальных счетов

Система национальных счетов (СНС) – адекватный в рыночной экономике национальный учет, завершаемый на макроуровне системой взаимосвязанных статистических показателей, построенной в виде определенного набора счетов и балансовых таблиц, характеризующих результаты экономической деятельности, структуру эконо­мики и важнейшие взаимосвязи в национальном хозяйстве.

Показатели СНС позволяют изучить темпы экономического роста и колебания экономической конъюнктуры, которые используются для анализа общих тенденций экономического развития страны за тот или иной период, оценки эффективности проводимой экономической политики, международных сопоставлений макроэкономических показателей.

Основная задача СНС состоит в том, чтобы дать упрощенное по форме, но вместе с тем полное по содержанию описание явлений и процессов, характеризующих экономическую жизнь страны (производства, образования и целения доходов, потребления, накопления, наличия и движение национального богатства), и проследить взаимосвязь между ними.

СНС используется для описания и анализа макроэкономических процессов в странах с рыночной экономикой.

Коэффициент фондов

Для характеристики распределения населения по доходу рассчитыва­ются также следующие показатели:

1) модальный доход, т. е. уровень дохода, наиболее часто встречающийся среди населения;

2) медианный доход – показатель дохода, находящегося в середине ран­жированного ряда распределения. Половина населения имеет доход ниже медианного, а вторая половина – выше;

3) коэффициент фондов ( 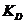), определяемый как соотношение между средними доходами населения в десятой и первой децильной группах:

Kd=Dcp10/Dcp1

где Dcp1и Dcp10 – среднедушевой доход в месяц соответственно у 10% населения, имеющего минимальный доход, и у 10% самой богатой его части.

Официальная черта бедности

При анализе степени социального расслоения особое значение имеет оценка бедности. Для измерения уровня бедности применяются различные подходы:

1) статистический (черта бедности устанавливается доходов, которыми располагают определенный процент самых малоимущих граждан);

2) нормативный (с определением прожиточного минимума i потребительской корзине). Этот метод определения уровня бедно применяется в Российской Федерации;

3) комбинированный (расходы на питание определяют нормативам, а остальные расходы – по их доле в общих расходах);

4) субъективный (на основе опросов, когда респондеь отмечают, какой доход они считают низким (высоким);

5) ресурсный (исходит из возможностей экономики обеспечить прожиточный минимум и др.).

Коэффициент эластичности

Для изучения зависимости объема потребления (результативного признака) от дохода и от уровня цен (факторных признаков, т.е. тех, которые оказывают влияние на результативный) в социальной статистике на практике используется коэффициент эластичности потребленияот изменения дохода (изменения цены) который показывает, насколько процентов возрастает (или снижается) потребление товаров и услуг при росте дохода на 1% (формула А.Маршалла):

Ky=(дельтаY/дельтаX)/(Y/X)=(дельтаY/Y)/(дельтаX/X)

где 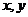– начальные доход и потребление; дельтаХ, дельтаY – их приращения за некоторый период (или при переходе от одной группы к другой).

Если коэффициент эластичности отрицательный, то с ростом доходов потребление «малоценных» (низкого качества) товаров уменьшается.

Если коэффициент эластичности больше единицы, то потребление растет быстрее доходов.

Если его значение равно единице, то между доходом и потреблением существует пропорциональная зависимость.

Если значение коэффициента меньше единицы, то потребление увеличивается медленнее, чем доход.

Задачи статистики в государственном и муниципальном управлении