Определение углов между двумя плоскостями

Две плоскости, пересекаясь, образуют четыре попарно равных двугранных угла. Если линия пересечения плоскостей на чертеже неизвестна, тогда угол между ними определяется как плоский угол между перпендикулярами, проведенными к плоскостям из произвольной точки пространства.

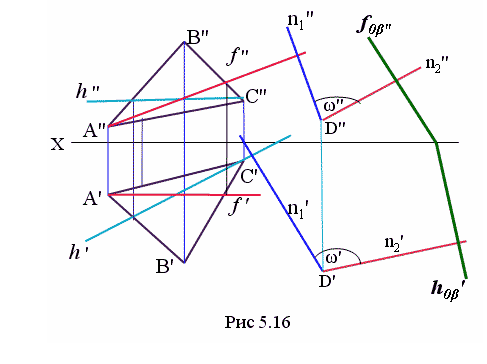
На рис. 5.16 заданы плоскость АВС (треугольником) и плоскость β, заданная следами. Из произвольной точки D проведены нормаль n₁ к плоскости АВС и нормаль n₂ к плоскости β. Далее надо определить угол между нормалями, опять же воспользовавшись способом замены плоскостей или способом вращения.

Если линия пересечения плоскостей на чертеже определена, тогда для нахождения величины двугранного угла можно применить способ замены плоскостей проекций, для чего надо линию пересечения (ребро) преобразовать в проецирующую прямую (см. рис. 2.1).

Теперь вы должны выполнить задачу 11 контрольной работы

Практическое занятие 6.
Метрические задачи

По данному разделу Вам предстоит решить задачи № 2, №9, №11.

В задаче №2 требуется определить натуральную длину отрезка и углы наклона прямой к плоскостям проекций.

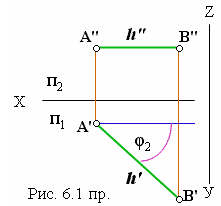
Решение задач подобного типа основано на свойствах прямых уровня.
На рис. 6.1 пр. задана горизонталь АВ. Ввиду того, что этот отрезок расположен параллельно горизонтальной плоскости, именно на ней он отображается в натуральную длину и, кроме того, угол φ₂является углом наклона этого отрезка к фронтальной плоскости проекций.

На рис. 6.2 пр. изображена фронталь. Этот отрезок на фронтальной плоскости проецируется в свою натуральную длину, а угол φ₁ является углом наклона фронтали к горизонтальной плоскости проекций.

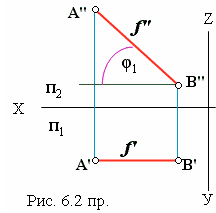
Для определения натуральной длины отрезков общего положения и углов их наклона к плоскостям проекций необходимо воспользоваться способом прямоугольного треугольника (см. рис. 5.7 для определения угла φ₂ и рис. 5.8 для определения угла φ₁ ).

Для решения задачи №9 необходимо воспользоваться способом замены плоскостей проекций (см. рис. 2.2)

Для решения задачи №11 надо из произвольной точки пространства опустить перпендикуляры (задать нормали) на заданные плоскости и определить угол между ними. Для задания нормалей n см. рис. 5.3 в случае, если плоскость задана тремя точками и рис. 5.4, если плоскость задана следами. Для определения угла надо воспользоваться способом вращения вокруг осей, расположенных параллельно к плоскостям проекций (см. рис. 2.4). Определить углы можно также решить и способом замены плоскостей, см. рис. 2.2.

По данной теме Вам необходимо выполнить в контрольной работе задачи № 2, №9, №11.

Тема 6