Способ вспомогательных сфер
Для построения линии пересечения двух поверхностей вращения целесообразно воспользоваться свойством, присущим поверхностям вращения, которое состоит в том, что две любы соосные поверхностивращения пересекаются по окружностям, проходящим через точки пересечения меридианов поверхностей. Меридианом называются линии, по которым плоскость, проходящая через ось вращения, пересекается с поверхностью. Если меридиан принадлежит плоскости, расположенной параллельно фронтальной плоскости проекций, он называется главным меридианом – по существу это фронтальный очерк поверхности.
В частном случае, если центр сферы находится на оси вращения другой поверхности вращения, то линией их пересечения является окружность. Число окружностей будет равно числу точек пересечения главных меридианов этих поверхностей.

На рис. 4.13 центр сферы принадлежит оси вращения конуса. Линией их пересечения являются две окружности. Свойство сферы пересекать поверхности вращения по окружностям позволяет использовать ее в качестве вспомогательной поверхности – посредника для нахождения линий пересечения между собой двух других поверхностей вращения.
Построить линии пересечения поверхностей с помощью вспомогательных секущих сфер можно двумя способами:
1. способом концентрических сфер;
2. способом эксцентрических сфер.
Способ концентрических сфер применяется для построения линии пересечения двух поверхностей вращения, оси которых пересекаются.

На рис. 4.14 представлены поверхность конуса и цилиндра, оси которых пересекаются. Для построения линии их пересечения в первую очередь отмечают точки пересечения контурных образующих. Затем строят семейство сфер с центром в точке пересечения осей заданных поверхностей. При этом минимальный радиус сферы принимается равным большему из двух вписанных сфер в эти поверхности. Максимальный радиус равен наибольшему расстоянию от центра пересечения осей поверхностей до точек взаимного пересечения контурных образующих.
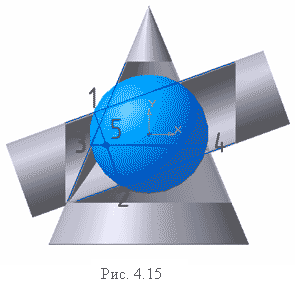
На рис. 4.15 промежуточная сфера пересекает поверхность цилиндра по окружности, отмеченной цифрами 1 2. Поверхность конуса эта же сфера пересекает по окружности 3 4. Точки пересечения этих окружностей отмечены цифрой 5. Эти точки являются элементом линии пересечения заданных поверхностей. Построив семейство таких сфер, полученные точки соединяют плавной кривой.
Способ эксцентрических сфер применяется для построения линии пересечения двух поверхностей, имеющих общую плоскость симметрии. При этом каждая поверхность должна иметь семейство окружностей, которые можно рассматривать как результат пересечения поверхности со сферой.
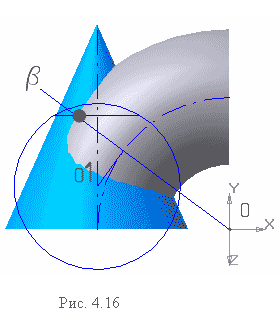
На рис 4.16 представлены торовая поверхность и поверхность конуса. Для построения лини пересечения этих поверхностей применяется способ эксцентрических сфер. Для нахождения центра вспомогательной сферы - посредника из точки О -центра тора проводят проецирующую плоскость β. Затем из точки пересечения проецирующей плоскости с осевой центров окружностей тора восстанавливают перпендикуляр до пересечения с осевой конуса – точка О1, которая и является центром вспомогательной секущей сферы. Окружность, по которой вспомогательная сфера пересечется с торовой поверхностью, лежит в плоскости β. Эта же сфера пересечет конус тоже по окружности (см. рис. 4.13). Точки пересечения построенных окружностей являются элементами линии пересечения заданных поверхностей. Для нахождения следующих точек задают новую плоскость β через центр О и повторяют предыдущие построения.
Теперь вы должны выполнить задачи 7,8,12 и 13 контрольной работы
Практическое занятие 5.
Позиционные задачи
По темам данного раздела Вам предстоит решить задачи на пересечение № 7, №8, №12, №13, №14 и №15.
При решении этих задач необходимо воспользоваться общим алгоритмом, приведенным в разделе 4.
В задаче №7 необходимо построить линию пересечения двух треугольников. Их пересечением является отрезок прямой. Любая прямая однозначно определяется двумя точками, следовательно, надо найти две точки, одновременно принадлежащие этим треугольникам. По существу, надо дважды решить задачу на пересечение прямой с плоскостью (см. компьютерную обучающую программу «Пересечение прямой с плоскостью»). Для решения надо через прямую одной плоскости задать вспомогательную проецирующую плоскость-посредник. При этом следует воспользоваться следующими рекомендациями. Вспомогательную проецирующую плоскость-посредник надо задавать через такую прямую одного треугольника, которая больше других проходит по площади другого заданного треугольника на обеих проекциях.
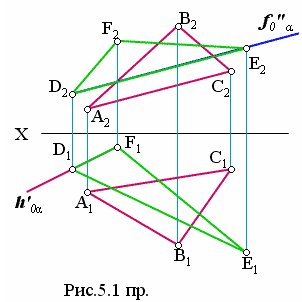
Пусть заданы два треугольника АВС и DFE (рис. 5.1 пр.). Правильнее задать вспомогательную плоскость-посредник f0 "α через отрезок DE , так как он проходит больше других отрезков по площади треугольникаАВС и на фронтальной плоскости и на горизонтальной. Самым неудачным выбором будет, если вспомогательную плоскость-посредник h'0 α задать через отрезок DF. Этот отрезок ни на горизонтальной, ни на фронтальной плоскостях проекций не проходит по площади другого треугольника АВС. Решение в любом случае будет найдено, но это произойдет далеко за пределами Вашего формата.
Пример решения подобной задачи приведен в компьютерной обучающей программе «пересечение плоскостей».
В связи с высоким быстродействием современных компьютеров, в выше упомянутой программе применено замедление построений, которое осуществляется Slider - движком. Передвигая движок вправо, вы можете замедлить процесс построения чертежа так, чтобы новые построения не оказались незамеченными.
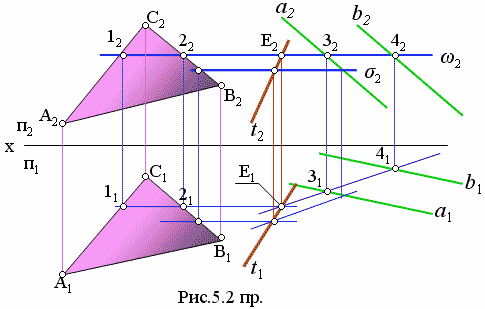
Вариант решения задачи с применением секущих плоскостей представлен на рис. 5.2 пр. В примере показано построение линии пересечения двух плоскостей, заданных треугольником АВС и двумя параллельными прямыми a и b. Согласно алгоритму задаем, например, вспомогательную плоскость- посредник ω2 . Эта плоскость пересечет АВС по линии 1-2 (12 22 – 11 21), а плоскость ab (a2 b2 - a1b1) по линии 3-4 (32 42 – 31 41). Отмечаем точку пересечения построенных линий – Е1 и по линии связи переносим ее на фронтальную плоскость - Е2 . Повторяем построения для плоскости σ2 при этом используем свойство параллельности, то есть, отмечаем одну точку пересечения σ2 с плоскостью АВС и одну с плоскостью a b. Проводим линии пересечения параллельно линиям 1-2 и 3- 4. Через построенные две общие точки строим линию пересечения плоскостей t (t1 t2).
В задаче №8 необходимо определить точку пересечения прямой с плоскостью. Пример решения задачи №8, в случае, если плоскость задана тремя точками, приведен в вышеупомянутой компьютерной программе «Пересечение прямой с плоскостью».
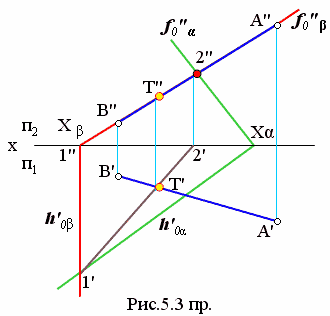
На рис. 5.3 пр. приведен пример решения этой задачи в случае, когда плоскость общего положения αзадана следами. Согласно алгоритму, задаем через прямую АВ вспомогательную проецирующую плоскость-посредник. В данном случае это фронтально проецирующая β. Ее фронтальный след f0 "β. Горизонтальный - h'0 β.
Пересечение вспомогательной β с прямой АВ – сама прямая. Для построения линии пересечения вспомогательной β с заданной плоскостью α отмечаем точки пересечения их следов – это точка 2 (2" 2') и точка 1 (1' 1"). Пересечение построенной линии (1' 2') с проекцией А' В' дает нам точку Т', которая является пересечением прямой АВ с плоскостью α. Ее фронтальную проекцию найдем по линии связи. Видимость прямой и плоскости можно определить по конкурирующим точкам.
Для решения задачи № 12 надо воспользоваться примерами из опорного конспекта см. подраздел 4.3
Для решения задачи №13 надо воспользоваться способом замены плоскостей проекций см. Практическое занятие 4.
Для решения задач № 14 и №15 необходимо воспользоваться алгоритмами, приведенными в подразделе 4.4, или воспользоваться источником [1, стр. 194-223].
По данной теме Вам необходимо выполнить в контрольной работе задачи № 7, №8, №12, №13, №14 и №15.
Тема 5
Метрические задачи
В разделе 4 отмечалось, что метрическими называются задачи, решение которых связано с нахождением характеристик геометрических фигур, измеряемых линейными и угловыми величинами. Все многообразие метрических задач в конечном итоге сводится к двум видам: задачам на определение расстояний между двумя точками и задачам на нахождение величины угла между двумя пересекающимися прямыми. К метрическим задачам также относятся задачи на построение геометрических фигур по наперед заданным размерам (задачи геометрического конструирования).
