Дифференциал первообразной
Тема: «Интегральное исчисление функции одной переменной»
Введение
Интеграл – одно из основных математических понятий, возникшее в связи с отысканием функции по заданной ее производной и вычислением площади криволинейной трапеции. Эти задачи привели к двум видам интеграла: неопределенному и определенному.
Изучение свойств и методов вычисления интеграла составляет задачу интегрального исчисления. Интегральное исчисление тесно связано с дифференциальным исчислением.
Первообразная. Неопределенный интеграл и его основные свойства
Основной задачей дифференциального исчисления является нахождение производной или дифференциала заданной функции.
Основной задачей интегрального исчисления является нахождение функции по заданной ее производной или дифференциалу.
Определение: Функция называется первообразной для данной функции, если ее производная равна данной функции.
Обозначение: 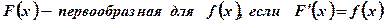 .
.
Вопрос: Является ли функция х2 первообразной для функции 2х?
Ответ: Функция х2 является первообразной для функции 2х, так как 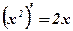 .
.
Вопрос: Какая из двух функций 3х2 или х3 является первообразной для другой?
Ответ: Функция х3 является первообразной для функции 3х2, так как 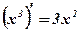 .
.
Функция 3х2 является производной от функции х3.
Вопрос: Какая из двух функций х5+7 или 5х4 является первообразной для другой?
Ответ: Функция х5+7 является первообразной для функции 5х4, так как 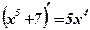 . Функция 5х4 является производной от функции х5+7.
. Функция 5х4 является производной от функции х5+7.
Упражнения:
Какая из двух функций является первообразной для другой?
1) 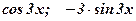 ; 2) ; 2) 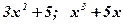 ; 3) ; 3) 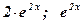 ; ; | 4) 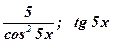 ; 5) ; 5) 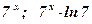 . . |
Дифференциал первообразной
Пусть функция 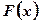 является первообразной для функции
является первообразной для функции 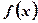 , то есть
, то есть 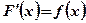 .
.
Воспользуемся определением дифференциала функции для вычисления дифференциала первообразной:
Дифференциалом функции называется произведение производной функции на дифференциал аргумента, то есть 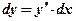 .
.
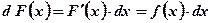
Вывод: Дифференциал первообразной для данной функции равен произведению данной функции на дифференциал аргумента.
Пример: Найти дифференциал первообразной для функции 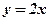 .
.
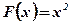 ;
; 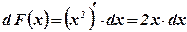 ;
; 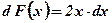 .
.
Задача: Являются ли функции 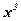 ;
; 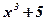 ;
; 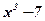 ;
; 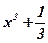 первообразными для функции
первообразными для функции 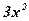 ?
?
Воспользуемся определением первообразной: 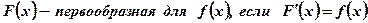 .
.
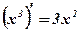 ;
; 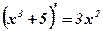 ;
; 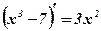 ;
; 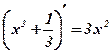 .
.
Ответ: Данные функции являются первообразными для функции 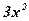 .
.
Вывод: Функция 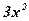 имеет бесконечное множество первообразных, отличающихся друг от друга на постоянную:
имеет бесконечное множество первообразных, отличающихся друг от друга на постоянную: 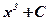 , С – постоянная.
, С – постоянная.
Теорема: Если функция 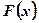 является первообразной для функции
является первообразной для функции 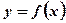 на интервале
на интервале 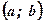 , то множество всех первообразных для функции
, то множество всех первообразных для функции 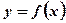 задается формулой
задается формулой 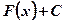 , где С – постоянная.
, где С – постоянная.
Замечание: Операция нахождения всех первообразных 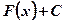 для данной функции
для данной функции 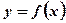 называется интегрированием этой функции. Интегрирование обозначается с помощью знака неопределенного интеграла
называется интегрированием этой функции. Интегрирование обозначается с помощью знака неопределенного интеграла 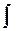 .
.
Определение: Неопределенным интегралом от данной функции называется совокупность ее первообразных:
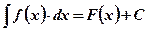 .
.
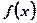 – подынтегральная функция;
– подынтегральная функция;
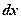 – дифференциал аргумента х;
– дифференциал аргумента х;
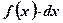 – подынтегральное выражение;
– подынтегральное выражение;
С – постоянная интегрирования.
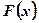 – первообразная для функции
– первообразная для функции 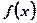 .
.
Пример:
|
|
Замечание:
- Интеграл называется неопределенным, так как результат интегрирования не однозначен.
- Графики всех первообразных
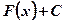 для функции
для функции 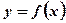 получаются из любого из них параллельным переносом вдоль оси Оу.
получаются из любого из них параллельным переносом вдоль оси Оу. - При нахождении для данной функции первообразной, удовлетворяющей начальным условиям, надо найти значение постоянной интегрирования.
Замечание:
- Дифференцирование (нахождение производной или дифференциала функции) и интегрирование являются взаимно обратными действиями.
Пример:
1) 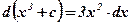 ;
; 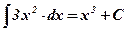 .
.
2) 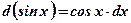 ;
; 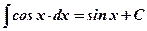 .
.
- Чтобы найти неопределенный интеграл от данной функции, нужно найти одну из ее первообразных и прибавить к ней произвольную постоянную.
- Для проверки правильности полученного результата необходимо помнить, что производная от результата интегрирования должна равняться подынтегральной функции.

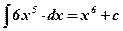 ;
;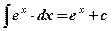 ;
;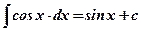 ;
;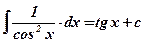 ;
;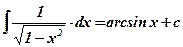 .
.