Определенный интеграл и его основные свойства
Задача: Найти приращения первообразных для данной функции  на данном интервале
на данном интервале  .
.
Решение:
 ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
;  .
.
Ответ:  .
.
Вывод: Приращение любой первообразной  для функции
для функции  при изменении аргумента х от 1 до 5 есть величина постоянная, равная 24.
при изменении аргумента х от 1 до 5 есть величина постоянная, равная 24.
Рассмотрим произвольную функцию  . Найдём приращения первообразных для функции
. Найдём приращения первообразных для функции 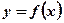 при изменении аргумента от
при изменении аргумента от 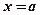 до
до 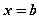 .
.
 - данная функция;
- данная функция;
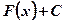 - все первообразные для функции
- все первообразные для функции  ;
;
 - значение любой первообразной для функции
- значение любой первообразной для функции  при
при 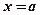 ;
;
 - значение любой первообразной для функции
- значение любой первообразной для функции  при
при 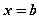 ;
;
 - приращение любой первообразной для функции
- приращение любой первообразной для функции  ;
;
 ;
;

Определение: Приращение любой первообразной для функции  при изменении аргумента х от
при изменении аргумента х от 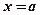 до
до 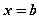 называется определённым интегралом в пределах от а до b от функции
называется определённым интегралом в пределах от а до b от функции  .
.
Обозначение: 
а - начальное значение аргумента, нижний предел интегрирования;
b - конечное значение аргумента, верхний предел интегрирования;
 - интервал интегрирования.
- интервал интегрирования.
Замечание: Интеграл в пределах от а до b от функции  называется определённым, так как приращение любой первообразной для данной функции (разность значений первообразной при конечном и начальном значениях аргумента) является числом.
называется определённым, так как приращение любой первообразной для данной функции (разность значений первообразной при конечном и начальном значениях аргумента) является числом.
Пример:
- Найти приращение любой первообразной для функции
 при изменении х от
при изменении х от 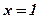 до
до 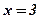 .
.
Решение:
 .
.
Ответ:  .
.
- Найти приращение любой первообразной для функции
 при изменении х от
при изменении х от  до
до  .
.
Решение:
 .
.
Ответ:  .
.
- Вычислить определённый интеграл в пределах от 0 до p от функции
 .
.
Решение:
 .
.
Ответ:  .
.
Правило вычисления определённого интеграла от данной функции
- Найти соответствующий неопределённый интеграл;
- В полученное его выражение подставить вместо х сначала верхний предел интегрирования, а затем нижний.
- Из первого результата вычесть второй.
Замечание:
1) При вычислении определённого интеграла от функции  пользуются записью:
пользуются записью:  (формула Ньютона-Лейбница).
(формула Ньютона-Лейбница).
2) Так как величина постоянной С не влияет на результат, её не пишут.
Пример: Вычислить:
1.  ;
;  ;
;
2.  ;
;  ;
;
3.  ;
;  .
.
Свойства определённого интеграла
- Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от этих функций:
 .
.
- Постоянный множитель подынтегральной функции можно вынести за знак определенного интеграла:
 .
. - При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
 .
. - Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
 .
.
- Интервал интегрирования можно разбивать на части:
 ,
,  .
.
Пример: Вычислить:
1)

2)

Упражнение №1: Вычислить определённые интегралы:
1)  ; ; | 2)  ; ; | 3)  ; ; |
4)  ; ; | 5)  ; ; | 6)  ; ; |
7)  ; ; | 8)  ; ; | 9)  ; ; |
10)  ; ; | 11)  ; ; | 12)  . . |
Ответы:
| 1) 168; | 2)  ; ; | 3)  ; ; | 4)  ; ; | 5)  ; ; | 6)  ; ; |
7)  ; ; | 8)  ; ; | 9)  ; ; | 10)  ; ; | 11)  ; ; | 12)  . . |
Упражнение №2: Вычислить определённые интегралы:
1)  ; ; | 2)  ; ; | 3)  ; ; |
4)  ; ; | 5)  ; ; | 6)  ; ; |
7)  ; ; | 8)  ; ; | 9)  ; ; |
10)  ; ; | 11)  ; ; | 12)  ; ; |
13)  ; ; | 14)  ; ; | 15)  ; ; |
16)  ; ; | 17)  ; ; | 18)  ; ; |
19)  ; ; | 20)  ; ; | 21)  . . |
Ответы:
