Взаимное положение двух прямых

Предмет «начертательная геометрия».Метод проецирования.Центральное и параллельное проецирование.Основные свойства.

Известны два метода проецирования: центральноеи параллельное.

1.Параллельное проецирование. Проецирование, при котором проецирующие лучи, проходящие через каждую точку объекта, параллельно выбранному направлению проецирования , называется параллельным.

Если точку S удалить от плоскости П в бесконечность,проецирующие лучи будут практически параллельны между собой.Тогда они пересекутся с плоскостью проекций П в точках А В С которые называются параллельными проекциями точек А В С между собой, получают треугольник А В С который будет уже параллельной проекцией треугольника АВС.

2.Центральное проецирование. Центральное проецирование заключается в проведении через каждую точку (А, В, С,…) изображаемого объекта и определённым образом выбранный центр проецирования(S) прямой линии (SA, SB,>… — проецирующего луча).

Свойство 1. Каждой точке пространства соответствует единственная проекция, но каждой точке плоскости проекций соответствует множество точек пространства, лежащих на проецирующей прямой.

Свойство 2. Проекция прямой есть прямая.

Инцидентность точки прямой – проекция точки, лежащей на прямой, будет лежать на проекции этой прямой. Суть метода заключается в следующем:пусть даны в пространстве треугольник ABC,плоскость П и произвольная точка S.Проведя из точки S прямые линии через вершины треугольника ABC до пересечения их с плоскостью П получают точки А В С .Соеденив прямыми линиями точки А В С получают центральную проекцию треугольника АВС.

Центральное и прямоугольное проецирование.Эпюр Монжа.

Прямоугольный или ортогональный носит название эпюр Монжа.

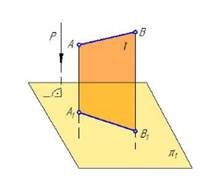
Если направление проецирования Р перпендикулярно плоскости проекций p₁, то проецирование называется прямоугольным или ортогональным. Четырехугольник АА₁В₁В задаёт плоскость γ, которая называется проецирующей, поскольку она перпендикулярна к плоскости π₁(γ⊥π₁). В дальнейшем будем использовать только прямоугольное проецирование.

Задание точки на комплексном чертеже Монжа. Принадлежность точки плоскости.

Комплексным чертежом называетсяплоский чертеж, состоящий из проекций изображаемого образа, размещенных в проекционной связи друг с другом. Линия проекционной связи всегда перпендикулярна оси проекций, разделяющие данные изображения.

Точка одно из основных понятий геометрии. При систематическом изложении геометрии точка обычно принимается за одно из исходных понятий.

Точка на комплексном чертеже Монжа может занимать общее положение, т.е. находиться вне плоскости проекций , и частное положение – находиться на одной из плоскостей проекций, сразу на двух плоскостях проекций или одновременно на трех.

К числу основных задач, решаемых на плоскости, относятся: построение прямой в плоскости, построение в плоскости некоторой точки, проверка принадлежности точки плоскости.

Точка принадлежит плоскости, если она лежит на прямой, принадлежащей плоскости.

Для того, чтобы в плоскости построить точку, необходимо в этой плоскости провести прямую и затем на прямой взять точку. При этом прямая расположена в плоскости, если она проходит через две точки, принадлежащие плоскости.

Задание прямой на комплексном чертеже монжа. Прямые общего и частного положения. Дать основные определения. Привести примеры.

Положение прямой линии определяется двумя ее точками. Поэтому пространственная прямая будет задана, если на чертеже имеются проекции двух ее точек, т.к. линии, проходящие через одноименные проекции этих точек, будут проекциями прямой. Прямая относительно плоскостей проекции может занимать различные положения.

Общего положения.

Прямая, не параллельная ни одной из плоскостей проекций, называется прямой общего положения.

Прямая ( l ) является прямой общего положения, если она не параллельна ни одной из плоскостей проекции.

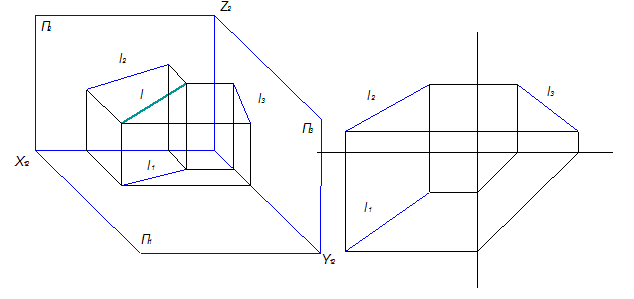Прямые частного положения.

Прямая, параллельная или перпендикулярная какой-либо плоскости проекций, называется прямой частного положения.

Прямые частного положения подразделяются на прямые уровня и проецирующие. К прямым уровня относятся горизонтальные, фронтальные и профильные.

Горизонтальная прямая параллельна плоскости П₁; фронтальная прямая параллельна плоскости П_2; профильная прямая параллельна плоскости П₃.

Прямые, перпендикулярные к одной плоскости проекций, - проецирующие Проецирующие прямые подразделяются на:

Горизонтально проецирующие прямые, перпендикулярные горизонтальной плоскости проекций (П₁), фронтально-проецирующие прямые, перпендикулярные фронтальной плоскости проекций (П₂), профильно-проецирующие прямые, перпендикулярные профильной плоскости проекций (П₃).

Взаимное положение двух прямых.

Две прямые в пространстве могут быть:

• параллельными;
• пересекающимися;
• скрещивающимися.

Параллельные прямые – прямые, пересекающиеся в несобственной точке.

Если прямые в пространстве параллельны, то их ортогональные проекции взаимно параллельны, или сливаются, или представляют собой точки, на одной из плоскостей проекций (Рисунок 2.12).

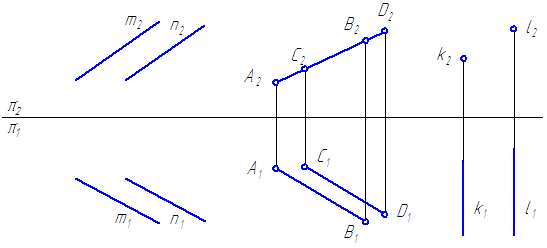
Рисунок 2.12 – Параллельные прямые

Пересекающиеся прямые – прямые, имеющие одну общую точку.

Если прямые в пространстве пересекаются, то на чертеже одноименные проекции прямых пересекаются, при этом проекции точки пересечения прямых лежат на одной линии проекционной связи и делят соответствующие проекции отрезков прямых в равных отношениях (Рисунок 2.13).

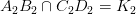
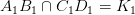
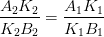
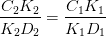
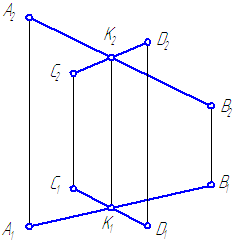
Рисунок 2.13 – Пересекающиеся прямые

Скрещивающиеся прямые – прямые, не имеющие общих точек и не удовлетворяющие признакам параллельных и пересекающихся прямых (Рисунок 2.14).

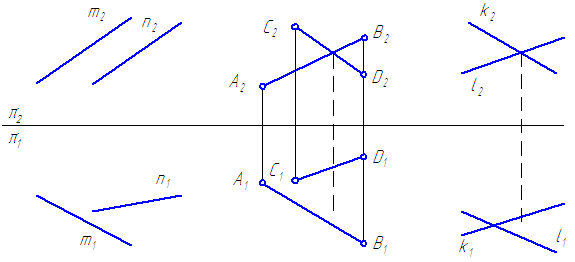
Рисунок 2.14 — Скрещивающиеся прямые