Задание 6. Проведение проектных уклонов профиля ПВО на графике естественного профиля на миллиметровке формат А4

Приложение 6.

Исходные данные: проектный профиль строится на уже построенном естественном профиле (Приложение 5). по проектным отметкам высот. Величина проектного уклона задается.

Решение. Проектная линия представляет собой ломаную линию, состоящую из отрезков прямых, соединяющих две соседние точки с заданными проектными отметками. Каждый такой участок характеризуется определенным проектным уклоном. Места изменения уклонов называются точками переломов проектной линии. Проектные отметки, уклоны и расстояния между смежными переломами связаны зависимостью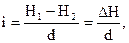
где i – уклон проектной линии на заданном участке (в тысячных), d – горизонтальное расстояние между смежными переломами проектной линии (в метрах), ΔH – превышение между проектными отметками смежных переломных точек (в метрах). Проектный профиль строится по проектным отметкам высот, которые вычисляются по формуле.

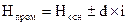
где Н_пром - проектная отметка промежуточной точки; H_осн - ближайшая основная проектная отметка;

d – расстояние от определяемой промежуточной точки до ближайшего перелома проектной линии.

В контрольной работе необходимо построить три проектных уклона:

- уклон между точками 0-2 равен -0,002

- уклон между точками 2-5 равен +0,001

- уклон между точками 5-6 равен 0,000

Порядок построения проектного профиля и вычисления промежуточных проектных отметок высот

для проектного уклона между точками 0-2

1) Проектная линия начинается с точки Н₀, равной естественной отметке т. 0

2) Проектная отметка т. 2 вычисляется как Н_{пром 2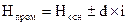} = = Н₀ – 0,002/d = , где d – сумма горизонтальных проложений между точками 0 – 1 и 1 – 2 (Ведомость 1, гр. 9)

для проектного уклона между точками 2-5

3) Проектная линия начинается с проектной отметки Н_{пром 2} точки 2, определенной выше

4) Проектная отметка т. 5 вычисляется как Н_{пром 5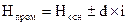} = = Н_{пром 2} + 0,001/d = , где d – сумма горизонтальных проложений между точками 2 – 3, 3 - 4 и 4 – 5 (Ведомость 1, гр. 9)

для проектного уклона между точками 5-6

5) Проектная линия начинается с проектной отметки Н_{пром 5} точки 5, определенной выше

6) Проектная отметка точки 6 равна проектной отметке точки 5 т.е. Н_{пром 6} = Н_{пром 5} =

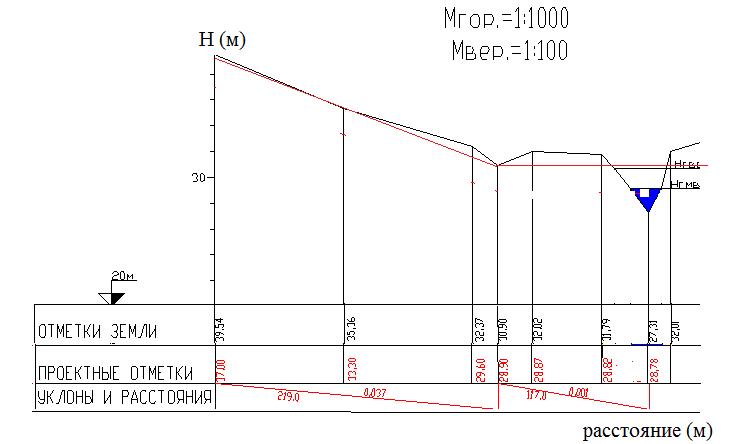
Пример 6. Построение естественного (черным цветом) и проектного (красным цветом) профилей заданной линии

Задание 7. Расчет элементов и пикетажного положения главных точек кривых трассы

Исходные данные. Для двух углов поворота трассы θ₁ = 20⁰+2∙n и θ₂ = 20⁰+(2∙n+10) и радиуса круговой кривой R=100 м вычислить элементы круговой кривой.

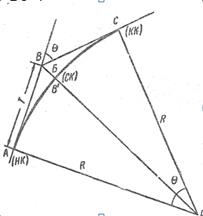
Решение. В местах поворота трассы автодороги ее сложные участки сопрягаются кривыми, чаще всего круговыми, то есть дугами определенного радиуса. Разбивка круговой кривой сводится к определению пикетного положения трех ее точек: начала (НК), конца (КК) и середины (СК).

1) Для заданных двух углов поворота трассы и радиуса кривой R=100 м вычислить элементы круговой кривой (тангенс T, кривую K, биссектрису Б, домер Д) по формулам:

Т=Rtg(θ/2), К=πR θº/180º, Б=√(Т²+R²) –R, Д=2Т – К.

θ₁= R=100 м, Т= К= Б = Д=

θ₂= R=100 м, Т= К= Б = Д=

2) Рассчитать пикетное положение начала и конца кривой трассы для двух углов поворота трассы при положении вершин углов поворота;

ВУ1 (ПК1+25.00м) и ВУ2 (ПК4+90.18м).

θ1=	ВУ1 (ПК1+25.00м)	θ2=	ВУ2 (ПК4+90.18м)
ВУ1	ПК1 + 25.00	ВУ2	ПК4+90.18
-Т		-Т
НК		НК
+К		+К
КК		КК
-Т		-Т
+Д		+Д
ВУ1	ПК1 +25.01	ВУ2	ПК4+90.18

Пример 7.

1. Для заданных двух углов поворота трассы θ и радиуса кривой R=100 м вычислить элементы круговой кривой (тангенс T, кривую K, биссектрису Б, домер Д) по формулам:

Т=Rtg(θ/2), К=πR θº/180º, Б=√(Т²+R²) –R, Д=2Т – К.

Например: θ= 57º 20', R=100 м, то Т=54,67 м, К=100.07 м, Б=13.97 м, Д= 9.28 м.

2. Вычислить пикетное обозначение начала и конца кривой для двух углов поворота трассы. Например:

ВУ1 ПК1 + 25.00

- Т 54.67

НК ПК0 + 70.33

+ К 100.07

КК ПК1 +70.40

- Т 54.67

ПК1 +15.73

+Д 9.28

ПК1 +25.01