ЛЕКЦИЯ 15. Спектр периодического сигнала
Периодический сигнал — это полезная математическая модель, позволяющая описывать некоторые существующие в природе процессы и их преобразования.
Периодический сигнал — это сигнал, определяемый выражением
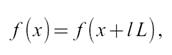
где L — период; l — любое целое число, принимающее положительные и отрицательные значения.
Как и всякая периодическая функция, он может быть разложен в ряд Фурье по тригонометрическим функциям:
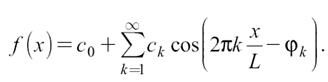
При этом периодический сигнал представляется суммой синусоидальных колебаний, частоты которых кратны основной частоте 1/L. Колебание с частотой 1/L называется первой гармоникой (k = 1), с частотой 2/L — второй гармоникой (k = 2) и т.д.
Данное выражение часто записывают в форме
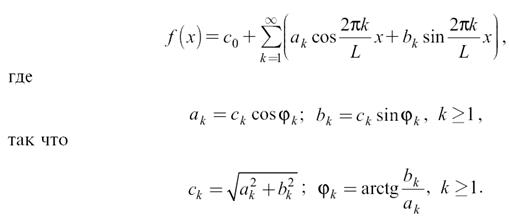
Коэффициенты ak и bk вычисляют по формулам
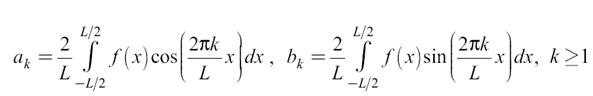
При этом постоянную составляющую c0 определяют по формуле
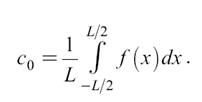
Ряд Фурье может быть также записан в комплексной форме:
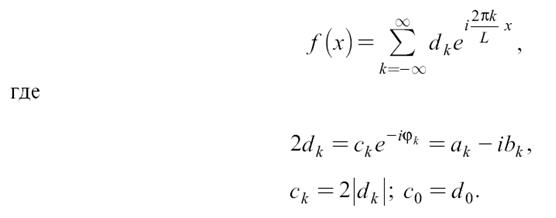
Величина dk называется комплексной амплитудой и может быть вычислена по формуле
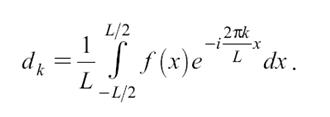
Как видим из формул, функция f(x) полностью определяется совокупностью величин ck и jk. Совокупность величин ck называется спектром амплитуд. Совокупность величин jk называется спектром фаз. Вообще говоря, спектром называют совокупность всех значений какой-либо величины, характеризующей систему или процесс. В физике изучают оптические спектры-разложения света по длинам волн, акустические спектры — характеристики звука, выражающие его частотный состав, и т.д. В теории сигналов изучаются спектры сигналов и систем вне зависимости от их физической природы. Заметим, что из общего определения спектра не следует, что в качестве спектральных компонент обязательно должны быть коэффициенты функции по тригонометрическому базису.
Введение рядов Фурье позволяет описывать периодические сигналы по всей оси –∞ ≤ x ≤ ∞. Они же широко применяются для описания сигналов, заданных на ограниченных временных или пространственных интервалах (финитных во времени или пространстве).
Например, пусть сигнал f(x) отличен от нуля на отрезке – L/2 ≤ x ≤ L/2, а вне этого отрезка равен нулю. Используем прием периодического продолжения и рассмотрим сигнал fL(x), заданный на всей оси (рисунок 15.1). Сигнал fL(x) является периодическим и может быть разложен в ряд Фурье в любой из введенных выше форм записи. В то же время на отрезке [– L/2; L/2] сигнал fL(x) совпадает с сигналом f(x), поэтому получим
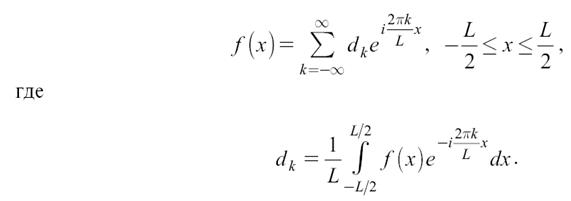
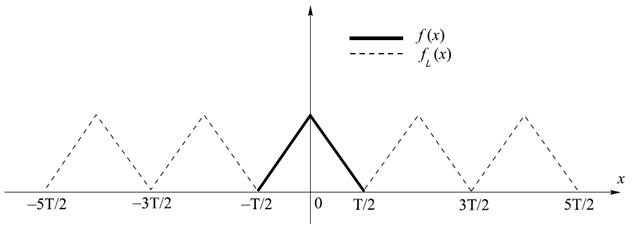
Рисунок 15.1 – Периодическое продолжение сигнала
Подчеркнем, что данные формулы дают спектральное представление финитного сигнала на ограниченном отрезке времени. Для решения целого ряда задач такое представление является достаточным, однако не следует забывать, что оно является в значительной мере формальным и не позволяет описывать сигнал f(x) полностью (на всей оси времени). Для полного описания непериодической функции следует использовать интеграл Фурье.
