Развертка цилиндрической и конической поверхностей. Геодезическая линия на поверхности
 Геодезическая линия - линия, соединяющая 2 точки по кратчайшему расстоянию на поверхности. Ей соответствует прямая линия на поверхности\
Геодезическая линия - линия, соединяющая 2 точки по кратчайшему расстоянию на поверхности. Ей соответствует прямая линия на поверхности\
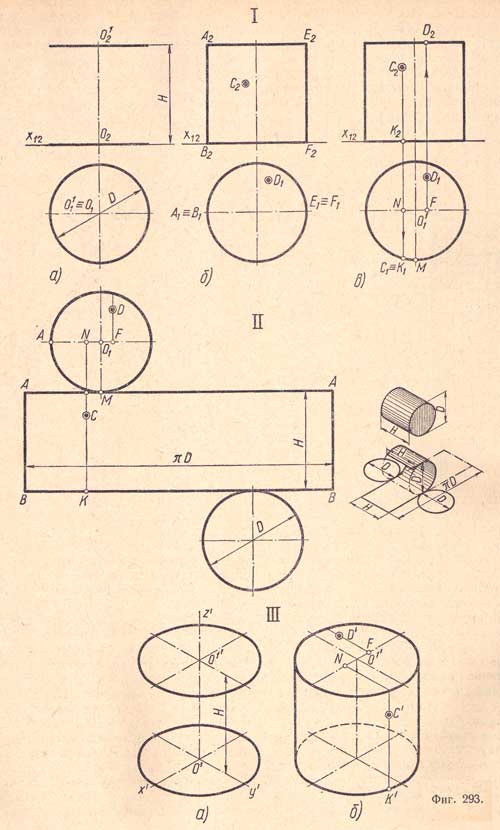
Развертка поверхности прямого кругового цилиндра.
Развертка представляет собой плоскую фигуру, составленную из развернутой в плоскость боковой поверхности цилиндра - прямоугольника, одна сторона которого равна высоте H цилиндра, а другая длине окружности основания (∏D), и двух оснований - кругов, диаметр которых равен диаметру окружности основания.
При построении развертки надо придерживаться следующего порядка:
а) определить длину окружности (∏D) основания;
б) построить развертку боковой поверхности (прямоугольник);
в) пристроить основания.
Перенос точки С на развертку боковой поверхности осуществляется при помощи размеров: дуги С1М и отрезка С2К2, а точки D на верхнем основании - при помощи размеров O'1F и FD1.

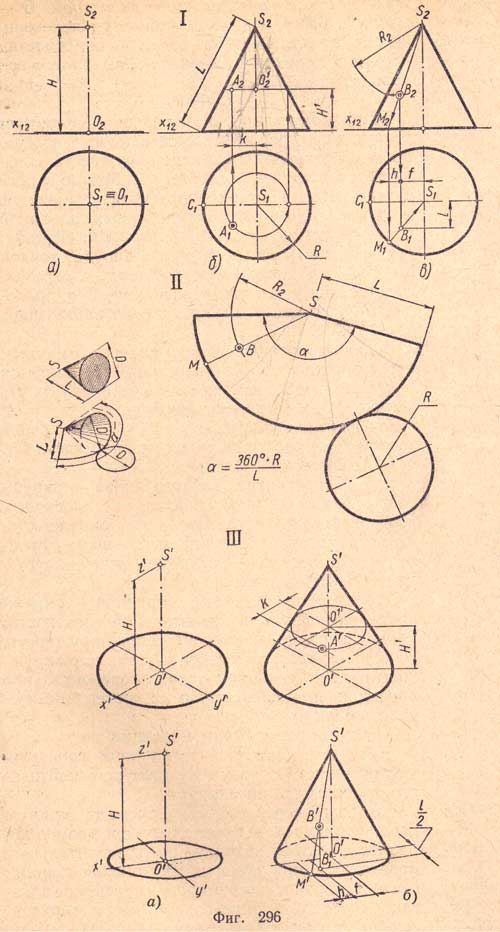
Развертка поверхности прямого кругового конуса - плоская фигура, составленная из сектора и окружности, диаметр которой равен диаметру окружности основания. Радиусом сек-гора является образующая конуса, а длина дуги равна длине окружности основания конуса. Угол сектора можно определить по формуле (a =360°R ÷ L) где R - радиус окружности основания конуса; L - образующая конуса. При построении развертки следует придерживаться следующего порядка:
а) определить угол а сектора;
б) построить развертку боковой поверхности конуса - сектор;
в) пристроить к любой точке, дуги сектора основание конуса - круг.
Перенос точки В на развертку боковой поверхности конуса осуществляется при помощи размеров С1М1 и R2, взятых с (фиг.296, I, в).

26. Построение развертки способом нормального сечения. В каких случаях применяется этот способ
Применяется для построения развёртки призматических гранных поверхностей,
Для построения развертки наклонной призмы, изображенной на рис. 9.3 необходимо найти истинные величины боковых ребер и сторон основания призмы. Призма расположена так, что ее боковые ребра параллельны плоскости П2 и проецируются на нее в натуральную величину. Стороны оснований являются горизонталями и проецируются на плоскость П1 без искажения. Таким образом, длины сторон каждой грани известны, однако этого еще недостаточно для построения истинной формы боковых граней.
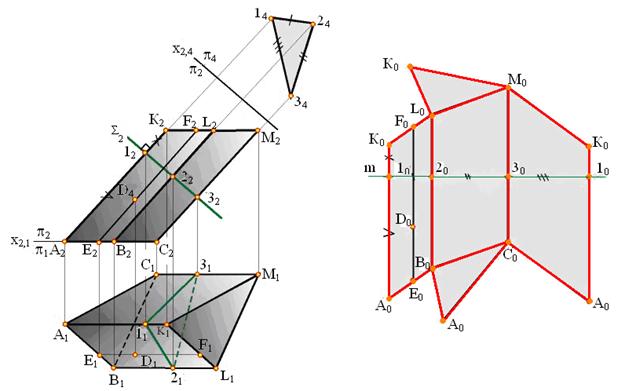
Рис. 9.3. Построение развертки призмы
Боковые грани наклонной призмы являются параллелограммами, которые не могут быть построены по четырем сторонам. Для построения параллелограмма необходимо помимо длины сторон знать еще его высоту. Для определения высот граней пересечем призму плоскостью ∑( ∑2), перпендикулярной к ребрам (способ нормального сечения), и определим истинную величину сечения путем замены плоскостей проекций. Стороны этого нормального сечения и будут высотами соответствующих граней. Теперь приступаем к построению развертки. На свободном месте чертежа проводим горизонтальную прямую m и откладываем на ней отрезки /1 - 2/ = /14 - 24/, /2 - З/ = /24 - 34/ и /3 - 1/ = /34 - 14/.
Через точки 1, 2, 3, 1 проводим перпендикуляры к прямой m и откладываем на них величины боковых ребер так, чтобы /А1/ = /А212/ и /1К/ = /12К2/, /В2/ = /В222/ и /2L/ = /22L2/ и т. п.
Соединив концы построенных отрезков, получим развертку боковой поверхности призмы. Присоединив к ней оба основания, получим полную развертку призмы. Построение на развертке точки 4, принадлежащей поверхности призмы, понятно из чертежа.
Образование аксонометрических проекций. Их виды в зависимости от коэффициэнтов искажения угла наклона проецирующих лучей к плоскости аксонометрических проекций. Стандартные аксонометрические проекции
Аксонометрические проекции.
1. Понятие об аксонометрических проекциях и их применение.Аксонометрическими (Аксонометрия в переводе с греческого языка («ахоп» — ось; «metreo» — измеряю) означает осемерное изображение.) проекциями называют изображения, полученные путем проектирования параллельными лучами фигуры (предмета) вместе с осями координат на произвольно расположенную плоскость, которую называют «аксонометрической» (или картинной). Обычно плоскость (или предмет) располагают так, чтобы на аксонометрической проекции предмета были видны три стороны: верхняя (или нижняя), передняя и левая (или правая).
Основным достоинством аксонометрических проекций является наглядность и представление о величине изображенного предмета, поэтому их применяют в качестве иллюстрации к чертежу для облегчения понимания конструктивной формы предмета.
Виды аксонометрических проекций.
В зависимости от направления проектирующих лучей аксонометрические проекции разделяются на: прямоугольные или ортогональные (проектирующие лучи перпендикулярны аксонометрической плоскости П') и косоугольные (проектирующие лучи наклонены к аксонометрической плоскости).
В зависимости от наклона осей координат к аксонометрической плоскости , а следовательно, от степени уменьшения размеров аксонометрических проекций отрезков, имеющих направление осей координат (Известно, что отрезок прямой, наклоненный к плоскости, проектируется на нее уменьшенным; чем больше будет угол наклона, тем меньших размеров будет проекция отрезка.), - все аксонометрические проекции делятся на три основных вида:
1) изометрические, т.е. одинакового измерения (оси z', х' и у' наклонены одинаково; следовательно, уменьшение размеров по направлению всех трех осей одинаковое);
2) диметрические, т. е. двойного измерения (две оси координат имеют один и тот же наклон, а третья - другой; следовательно, уменьшение размеров по этим двум осям будет одно и то же, а по третьей оси - другое);
3) триметрические, т.е. тройного измерения (все оси имеют разный наклон; следовательно, уменьшение размеров по направлению всех трех осей разное).
В машиностроительном черчении из прямоугольных аксонометрических проекций чаще всего применяют изометрическую и диметриче-скую, а из косоугольных - диметрическую, которую иначе называют фронтальной диметрической проекцией.
3. Изображение аксонометрических осей и показатели искажения. В изометрической проекции углы между аксонометрическими осями х' , у' и z'одинаковы (по 120°); ось z' расположена вертикально; следовательно, оси х'и у' наклонены к горизонтальной линии на угол 30° .
При таком положении осей показатели искажения для всех осей одинаковы и равны 0,82.
Показателем искажения называют отношение размера аксонометрической проекции отрезка, имеющего направление какой-либо оси координат, к его действительному размеру. Например, при действительном размере 100 мм и показателе искажения 0,82 размер аксонометрической проекции равен 100 × 0,82 = 82 мм.
В диметрической проекции угол между аксонометрическими осями z' и х'равен 97°10', а углы между аксонометрическими осями х' и у', а также z' и у'одинаковы, т.е. по 131°25'. Аксонометрическая ось z' имеет вертикальное положение, следовательно, ось х' наклонена к горизонтальной линии на угол7°10' а ось у' на угол 41° 25' (фиг.271,б).
При таком наклоне аксонометрических осей показатель искажения для осей z'и х' равен 0,94, а для оси у' - 0,47.
Во фронтальной диметрической проекции угол между аксонометрическими осями z' и х' равен 90°, а углы между аксонометрическими осями х' и у', а также между аксонометрическими осями z' и y' одинаковы, т. е. по 135°. Осьz' имеет вертикальное положение, следовательно, ось х' будет иметь горизонтальное положение, а ось у' наклонена к горизонтальной линии на угол 45° (фиг.271,в).
Показатели искажения по аксонометрическим осям х' и z' равны 1,0 а по осиу' - 0,5.
Такую фронтальную диметрическую проекцию называют кабинетной; ее рекомендуется применять тогда, когда хотят показать без изменения очертания фигур, расположенных в плоскостях, параллельных фронтальной плоскости проекций.
