Понятие о конформном отображении

Пусть однозначная функция 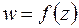определена в некоторой области 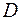и пусть точки и принадлежат области .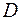

Определение.Если существует конечный предел отношения , когда по любому закону стремится к нулю, то:

1) этот предел называется производной функции в точке и обозначается символом

; (4.1)

2) в этом случае функция называется дифференцируемой в точке .

Все правила и формулы дифференцирования функции действительного переменного остаются в силе и для функций комплексного переменного.

Теорема.Для того, чтобы функция была дифференцируема в точке , необходимо и достаточно, чтобы:

1) действительные функции и были дифференцируемы в точке *) ;

2) в этой точке выполнялись условия

, (4.2)

называемые условиями Коши-Римана (C.-R.) или Даламбера-Эйлера.

При выполнении условий (C.-R.) производная функции может быть найдена по одной из следующих формул:

(4.3)

Приведем два определения, имеющих фундаментальное значение в теории функции комплексного переменного.

Определение.Функция называется аналитической в области,если она дифференцируема в каждой точке этой области.

Определение.Функцияназывается аналитической в точке , если она является аналитической в некоторой окрестности точки , т.е. если функция дифференцируема не только в данной точке, но и в ее окрестности.

Из приведенных определений видно, что понятия аналитичности и дифференцируемости функции в области совпадают, а аналитичность функции в точке и дифференцируемость в точке – разные понятия. Если функция аналитична в точке, то она, безусловно, дифференцируема в ней, но обратное может и не иметь места. Функция может быть дифференцируема в точке, но не быть дифференцируемой ни в какой окрестности этой точки, в таком случае она не будет аналитической в рассматриваемой точке.

Условием аналитичности функции в области является выполнимость условий Коши–Римана для всех точек этой области.

Связь аналитических функций с гармоническими. Любая ли функция двух переменных 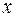и 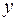может служить действительной и мнимой частью некоторой аналитической функции?

Если функция аналитическая в области 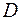, то функции и являются гармоническими, т.е удовлетворяют уравнению Лапласа.

и .

Однако если функции и являются произвольно выбранными гармоническими функциями, то функция , вообще говоря, не будет аналитической, т.е. условия для них не всегда будут выполняться.

Можно построить аналитическую функцию по одной заданной гармонической функции (например, ), подобрав другую так, чтобы удовлетворялись условия . Условия (4.2) позволяют определить неизвестную функцию (например, ) по ее двум частным производным или, что то же самое, по ее полному дифференциалу. Отыскивание гармонической функции по ее дифференциалу есть известная из действительного анализа задача интегрирования полного дифференциала функции двух переменных.

Геометрический смысл модуля и аргумента производной. Пусть функция 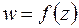дифференцируема в области 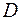и . Функция отобразит точку плоскости в точку плоскости 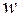, кривую 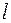, проходящую через точку 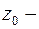в кривую 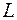, проходящую через 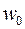(рис.4.1).

Модуль производной есть предел отношения бесконечно малого расстояния между отображенными точкам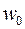и и к бесконечно малому расстоянию между их прообразами и . Поэтому величину можно рассматривать геометрически как коэффициент растяжения (если ) в точке при отображении области 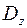в области , осуществляемом функцией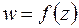

Рис. 4.1

В каждой точке области в каждом направлении коэффициент растяжения 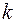будет свой. Для аргумента производной можно записать

,

где и это соответственно углы и , которые векторы и образуют с действительной осью (рис.4.1). Пусть и углы, образованные касательными к криво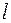й и 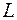в точках и 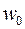с действительной осью. Тогда при , а , поэтому определяет угол, на который нужно повернуть касательную к кривой 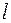в точке , чтобы получить направление к касательной к кривой 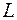в точке .

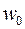Если рассмотреть две кривые и , и , то углы и (рис. 4.1) между их касательными, вообще говоря, неравные.

Определение.Отображение области 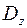на область , обладающее свойствами постоянства растяжений ( ) в любом направлении и сохранения (или консерватизма) углов между двумя кривыми, пересекающимися в точке , называется конформным (подобным в малом). Отображение, осуществляемое аналитической функцией, является конформным во всех точках, в которых .

УПРАЖНЕНИЯ

55. Показать, что функция дифференцируема и аналитична во всей комплексной плоскости. Вычислить ее производную.

Решение. Найдем и . По определению имеем . Следовательно, .

, ,

Откуда , .

Как видно, частные производные непрерывны на всей плоскости, и функции и дифференцируемы в каждой точке плоскости. Условия выполняются. Следовательно, 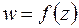дифференцируема в каждой точке плоскости, а значит, и аналитична на всей плоскости . Поэтому производную можно найти по одной из формул (4.3):

.

Наконец, производная может быть найдена по правилам формального дифференцирования: .

56. Выяснить, является ли аналитической функция:

а) ; б) ?

Решение. а) Так как , то , откуда . Как видно, первое условие (4.2) не выполняется ни при каких 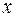и 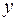. Следовательно, функция не дифференцируема ни в одной точке плоскости, а поэтому и не аналитична.

б) Имеем . Функция и дифференцируемы в каждой точке плоскости, ибо их частные производные непрерывны во всей плоскости. Но условия не выполняются ни в какой точке плоскости, кроме точки , где все частные производные равны нулю. Следовательно, функция дифференцируема только в одной точке, но не является аналитической в ней, так как по определению требуется дифференцируемость в окрестности данной точки.

Таким образом, функция не является аналитической ни при каком значении . Из приведенного примера ясно, что аналитичность функции в точке более сильное требование, чем дифференцируемость ее в этой точке.

57. Существует ли аналитическая функция, для которой ?

Решение. Проверим, является ли функция гармонической. С этой целью находим

,

и . Из последнего соотношения следует, что не может быть действительной, а также и мнимой частью аналитической функции.

58. Найти, если это возможно, аналитическую функцию по ее действительной части .

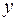Решение.Прежде проверим, является ли функция гармонической. Находим , , , и . Гармоническая на всей плоскости функция сопряжена с условиями Коши-Римана , . Из этих условий получаем , . Из первого уравнения системы находим интегрированием по , считая 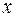постоянным.

,

где произвольная функция, подлежащая определению. Найдем отсюда и приравняем к выражению , ранее найденному: . Получим дифференциальное уравнение для определения функции , откуда

. Итак, . Тогда

.

59. Восстановить аналитическую функцию 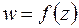по известной ее мнимой части и при дополнительном условии .

Решение. Опуская проверку данной функции на гармоничность, находим , . Следовательно, .

Дифференцируя 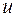по 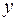, получим . Но с другой стороны, по второму из условий (C. - R.) . Сопоставляя последние два равенства, получим дифференциальное уравнение относительно функции , откуда следует, что и .

Итак, , следовательно,

или .

Как видно из приведенных примеров аналитическая функция определяется по своей действительной или мнимой части с точностью до произвольной постоянной. Задание дополнительного условия – значения функции в точке позволяет определить аналитическую функцию единственным образом.

По условию , воспользуемся этим для определения , откуда и .

60. Найти коэффициент подобия 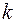и угол поворота 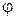в точке при отображении :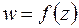

а) 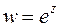, ; б) , .

Решение. а) Найдем и ее частное значение в точке . Значит, коэффициент подобия , т.е. отображение производится сжатие в точке , а , т.е. в данной точке происходит вращение на угол по часовой стрелке.

б) , откуда следует, что коэффициент растяжения , а угол поворота .

61. Каково отображение, осуществляемое функцией ?

Решение. . Функция аналитична во всей плоскости, но в точке . Поэтому отображение, осуществляемое этой функцией, конформно во всех точках, за исключением точки . Так как , то лучи и , выходящие из точки и образующие между собой угол , отображаются соответственно в лучи и , образующие между собой угол . Поэтому в точке конформность отображения нарушается в силу того, что нарушается свойство консерватизма углов: углы не сохраняются, а утраиваются.