Алгебраические фракталы
Это самая крупная группа фракталов. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Интерпретируя нелинейный итерационный процесс, как дискретную динамическую систему, можно пользоватся терминологией теории этих систем: фазовое пространство, аттрактор и т.д. [2].
Фазовое пространство — пространство, на котором представлено множество всех состояний системы, так, что каждому возможному состоянию системы соответствует точка фазового пространства.
Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или как говорят - аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния.
Таким образом, фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры.
В качестве примера рассмотрим множество Мандельброта.
Множество Мандельброта — это фрактал, определённый как множество точек c на комплексной плоскости, для которых итеративная последовательность
z0 = 0
zn+1 = zn2+c
не уходит в бесконечность.
Таким образом, вышеуказанная последовательность может быть раскрыта для каждой точки c на комплексной плоскости следующим образом:
c = x + i ∙ y
Z0 = 0
Z1 = Z02 + c
= x + i ∙ y
Z2 = Z12 + c
= (x + i ∙ y)2 + x + i ∙ y
= x2 + 2∙i∙x∙y – y2 + x + i ∙ y
= x2 – y2 + x + (2 ∙ x ∙ y + y) ∙ i
Z3 = Z22 + c = …
и так далее.
Если переформулировать эти выражения в виде итеративной последовательности значений координат комплексной плоскости x и y, т. е. заменив zn на xn + i ∙ y, а c на p + i ∙ q, мы получим:
| xn+1 = xn2 – yn2 + p yn+1 = 2∙xn ∙ yn + q | (*) |
Суть метода построения множества Мандельброта состоит в следующем. Для каждого пикселя, отображающего некоторую точку с координатами (a, b), проводят серию вычислений по формулам (*). При этом исходные значения x0 и y0 для каждой новой точки (a, b) изначально всегда равны нулю. На каждом шаге, кроме очередных значений xi+1 и yi+1, вычисляют величину ri =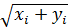 
. Эта величина представляет собой не что иное, как расстояние от точки (xi, yi) до начала координат. Точка (a, b) считается принадлежащей множеству Мандельброта, если она в процессе вычислений никогда не удаляется от начала координат на критическое расстояние, большее или равное двум. Такой пиксель окрашивается в черный цвет. Для всех прочих значений a и b величина ri может переходить запретный рубеж в две единицы за разное количество шагов. В зависимости от этого, точку окрашивают в соответствующий цвет.
Критическое значение при программировании имеет скорость вычислений. Существенно влияют на время расчетов операции возведения в степень и извлечение квадратного корня. Возведение в квадрат целесообразно заменить умножением. Возводить координаты в квадрат следует лишь один раз, сохраняя результаты в промежуточных переменных (x2 и y2). От извлечения квадратного корня вообще следует отказаться. Вместо самого значения расстояния ri можно вычислять лишь сумму квадратов x2 + y2, сравнивая ее не с двойкой, а с четверкой.
Функции для генерации множества Мандельброта приведены ниже. В зависимости от полученного значения k (обратного счетчика итераций), очередная точка закрашивается в соответствующий цвет (в данном случае точка окрашивается в различные градации серого цвета). Если k оказывается равным нулю, то точка с координатами (a, b) принадлежит множеству Мандельброта. В отношении всех прочих точек имеет значение, насколько велико или мало значение k. Оно характеризует скорость убегания величины ri за дозволенный предел при данных значениях a и b.
private Color GetColor(double a, double b)
// Функция, возвращающая цвет точки (a, b)
{
double x = 0, y = 0, r = 0;
//количество итераций для каждой точки
int k = 100;
while ((r<4) && (k>0))
{
Double x2 = x * x;
Double y2 = y * y;
Double xy = x * y;
x = x2 - y2 + a;
y = 2 * xy + b;
r = x2 + y2;
k--;}
k = 255*k/100;
Color p = Color.FromArgb(255, k, k, k);
return p;
}
private void Mbut_Click(object sender, EventArgs e)
//Функция построения множества Мандельброта
//в квадрате размером 400 x 400 пикселей
{
//Определение области построения
const double xmin = -2;
const double xmax = 1;
const double ymin = -1.5;
const double ymax = 1.5;
//длинна стороны квадрата
const int n = 400;
//определение приращения по x и по y
double hx = (xmax - xmin) / n;
double hy = (ymax - ymin) / n;
Bitmap bmp;
bmp = new Bitmap(this.ClientSize.Width, this.ClientSize.Height);
double x = xmin;
double y = ymax;
for (int j = 1; j < n; j++)
{
for (int i = 1; i < n; i++)
{
Color c = GetColor(x, y);
bmp.SetPixel(i, j, c);
x = x + hx;
}
y = y - hy;
x = xmin;
}
Graphics gr = CreateGraphics();
gr.DrawImage(bmp, 0, 0);
}
Вышеописанный алгоритм дает приближение к так называемому множеству Мандельброта. Множеству Мандельброта принадлежат точки, которые в течение бесконечного числа итераций не уходят в бесконечность (точки, закрашенные в черный цвет). Точки, принадлежащие границе множества (именно там возникает сложные структуры) уходят в бесконечность за конечное число итераций, а точки, лежащие за пределами множества, уходят в бесконечность через несколько итераций (белый фон).
Пример работы программы и приближения к множеству Мандельброта в диапазоне для x от -2 до 1 и для y от -1,5 до 1,5 приведен на рис. 1.12.
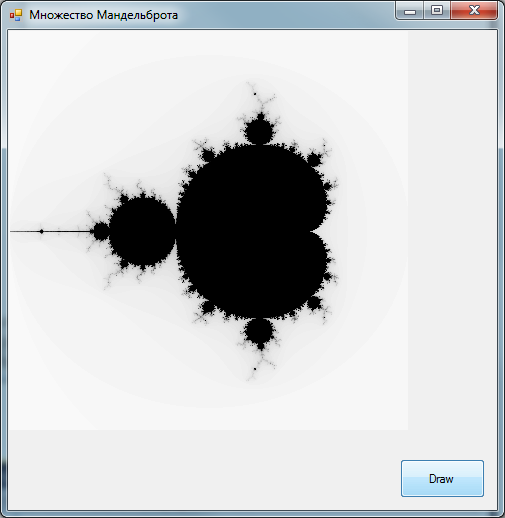
Рис. 1.12. Множество Мандельброта
Используя туже самую итеративную последовательность zn+1 = zn2+c, что и для построения множества Мандельброта, можно построить другой алгебраический фрактал: множество Жюлиа. Множество Жюлиа получается, если зафиксировать в формуле значение комплексной константы (a+i∙b), которая будет одинакова для всех точек, а начальные значения x и y принимать равными значениям координатам вычисляемой точки. В этом случае, код функции получения цвета точки будет выглядеть следующим образом:
private Color GetColorJ(double x, double y)
{
//задаем произвольно начальную точку
double a = -0.55, b = -0.55
double r = 0;
int k = 100;
while ((r < 4) && (k > 0))
{
Double x2 = x * x;
Double y2 = y * y;
Double xy = x * y;
x = x2 - y2 + a;
y = 2 * xy + b;
r = x2 + y2;
k--;
}
k = 255 * k / 100;
Color p = Color.FromArgb(255, k, k, k);
return p;
}
Еще одним известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.