Приведём решение методом координат.
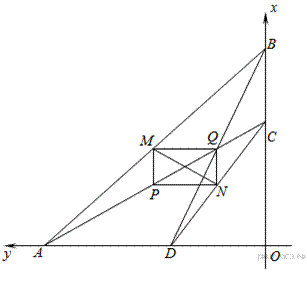 Пусть сторона BC лежит на оси Ox, а сторона AD лежит на оси Oy. Найдем координаты вершин четырехугольника:
Пусть сторона BC лежит на оси Ox, а сторона AD лежит на оси Oy. Найдем координаты вершин четырехугольника: 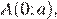
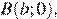
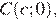
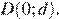
Пусть M — середина AB, и N — середина CD. По формуле нахождения координат середины отрезков, найдем координаты точек M и N: 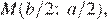
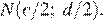 Определим длину отрезка MN через координаты его концов:
Определим длину отрезка MN через координаты его концов: 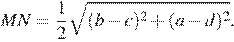
Пусть точки P и Q — середины диагоналей AC и BD. Аналогично получаем: 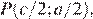
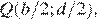
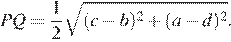
Тема самым, что  Следовательно, искомая длина равна 1 метру.
Следовательно, искомая длина равна 1 метру.
Критерии проверки:
Источник: Тренировочные работы. Иркутск — 2013, вариант 2.
Задание 24 № 311717
10.Каждое основание 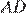 и
и 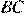 трапеции
трапеции 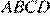 продолжено в обе стороны. Биссектрисы внешних углов
продолжено в обе стороны. Биссектрисы внешних углов 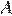 и
и 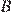 этой трапеции пересекаются в точке
этой трапеции пересекаются в точке 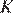 , биссектрисы внешних углов
, биссектрисы внешних углов  и
и 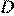 пересекаются в точке
пересекаются в точке 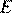 . Найдите периметр трапеции
. Найдите периметр трапеции 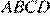 , если длина отрезка
, если длина отрезка 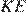 равна 28.
равна 28.
Решение.
Углы 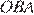 и
и 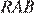 — односторонние при параллельных прямых
— односторонние при параллельных прямых 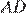 и
и 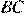 и секущей
и секущей 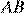 . Значит их сумма равна 180°.
. Значит их сумма равна 180°.
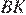 — биссектриса угла
— биссектриса угла 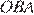 ;
; 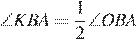 .
.
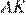 — биссектриса угла
— биссектриса угла 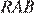 ;
; 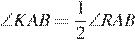 .
.
Тогда сумма углов 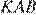 и
и 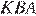 равна 90°, значит треугольник
равна 90°, значит треугольник 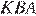 — прямоугольный. Аналогично, треугольник
— прямоугольный. Аналогично, треугольник 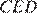 — прямоугольный. Точки
— прямоугольный. Точки 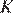 и
и 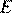 — точки пересечения биссектрис внешних углов трапеции
— точки пересечения биссектрис внешних углов трапеции 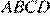 , значит,
, значит, 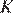 и
и 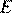 — равноудалены от параллельных прямых
— равноудалены от параллельных прямых 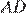 и
и 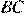 . (Точка
. (Точка 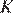 равноудалена от сторон угла
равноудалена от сторон угла 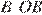 и
и 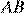 , и равноудалена от сторон угла
, и равноудалена от сторон угла 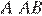 и
и 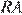 , т. к. лежит на биссектрисах соответствующих углов).
, т. к. лежит на биссектрисах соответствующих углов).
Таким образом, прямая 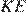 параллельна прямым
параллельна прямым 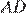 и
и 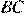 , и по теореме Фалеса точки
, и по теореме Фалеса точки 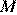 и
и 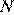 , середины сторон
, середины сторон 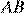 и
и 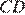 и
и 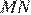 — средняя линия трапеции (по определению).
— средняя линия трапеции (по определению).
Из прямоугольного треугольника 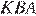 ,
, 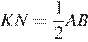 (
( 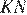 — медиана, проведенная к гипотенузе). Из прямоугольного треугольника
— медиана, проведенная к гипотенузе). Из прямоугольного треугольника 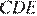 ,
, 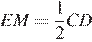 (
( 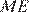 — медиана, проведенная к гипотенузе.
— медиана, проведенная к гипотенузе. 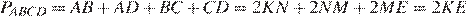
Значит, периметр трапеции  равен 56.
равен 56.
Ответ: 56.
Критерии проверки:
Источник: Пробный экзамен. Санкт-Петербург — 2013, вариант 1.
Задание 24 № 311712
11.Найдите площадь выпуклого четырёхугольника с диагоналями 8 и 5, если отрезки, соединяющие середины его противоположных сторон, равны.
Решение.
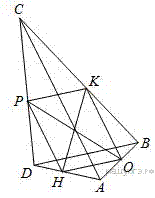
Пусть  — данный четырёхугольник,
— данный четырёхугольник,  — середина стороны
— середина стороны 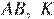 — середина стороны
— середина стороны 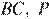 — середина стороны
— середина стороны 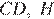 — середина стороны
— середина стороны 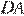 . Проведём диагонали
. Проведём диагонали 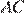 и
и 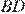 и отрезки
и отрезки 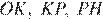 и
и 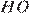 , последовательно соединяющие середины сторон четырёхугольника. Тогда, по свойству средней линии треугольника, отрезки
, последовательно соединяющие середины сторон четырёхугольника. Тогда, по свойству средней линии треугольника, отрезки 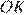 и
и 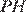 параллельны диагонали
параллельны диагонали 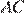 и равны её половине, а отрезки
и равны её половине, а отрезки 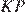 и
и 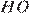 параллельны диагонали
параллельны диагонали 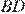 и равны её половине. Поэтому
и равны её половине. Поэтому 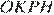 — параллелограмм. А так как, по условию задачи, его диагонали
— параллелограмм. А так как, по условию задачи, его диагонали 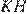 и
и 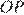 равны, то
равны, то 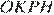 — прямоугольник, и угол
— прямоугольник, и угол 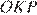 — прямой. Отсюда следует, что и угол между диагоналями
— прямой. Отсюда следует, что и угол между диагоналями 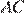 и
и 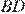 тоже прямой, и, следовательно, площадь четырёхугольника
тоже прямой, и, следовательно, площадь четырёхугольника 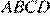 будет равна половине произведения его диагоналей, то есть
будет равна половине произведения его диагоналей, то есть 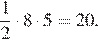
Ответ: 20.
Критерии проверки:
Источник: Тренировочные работы. Иркутск — 2013, вариант 3.
Задание 24 № 128
12. 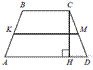 В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
Решение.
Так как AB = CD, то трапеция является равнобедренной. Опустим перпендикуляр BL из точки B на большее основание AD. Прямоугольные треугольники ABL и CHD равны по гипотенузе и прилежащему острому углу, поэтому AL = HD. Средняя линия равна полусумме оснований:
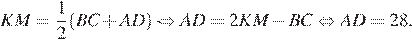
Так как AL = HD, имеем: 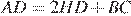 , значит,
, значит, 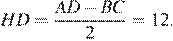
Ответ: HD = 12.
Критерии проверки:
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1309.
Задание 24 № 339511
13. 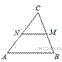
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Решение.
Поскольку 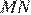 — средняя линия треугольника
— средняя линия треугольника 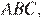
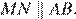
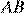 и
и 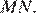 Рассмотрим треугольники
Рассмотрим треугольники  и
и 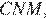 углы
углы 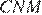 и
и 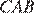 равны как соответствующие углы при параллельных прямых, угол
равны как соответствующие углы при параллельных прямых, угол  — общий, следовательно, эти треугольники подобны. Откуда коэффициент подобия
— общий, следовательно, эти треугольники подобны. Откуда коэффициент подобия 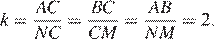 Площади подобных фигур соотносятся как квадрат коэффициента подобия, поэтому
Площади подобных фигур соотносятся как квадрат коэффициента подобия, поэтому 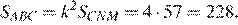 Найдём площадь четрыёхугольника
Найдём площадь четрыёхугольника 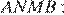
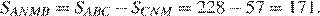
Ответ: 171.
Критерии проверки:
Задание 24 № 315116
14. 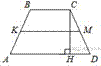
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
Решение.
В трапеции средняя линия равна полусумме оснований, поэтому можем найти большее основание 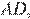 зная
зная 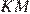 и
и 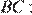
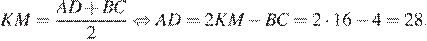
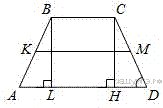
Проведём в трапеции вторую высоту 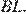 Трапеция равнобедренная, поэтому
Трапеция равнобедренная, поэтому 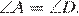 Рассмотрим два треугольника:
Рассмотрим два треугольника: 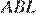 и
и 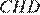 , они прямоугольные, имеют равные углы и
, они прямоугольные, имеют равные углы и 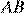 равно
равно 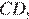 следовательно, эти треугольники равны. Таким образом, равны отрезки
следовательно, эти треугольники равны. Таким образом, равны отрезки 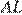 и
и 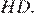
Также рассмотрим четырёхугольник 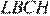 , все углы в нём — прямые, следовательно, это прямоугольник, значит,
, все углы в нём — прямые, следовательно, это прямоугольник, значит, 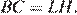
Теперь найдём длину отрезка 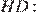
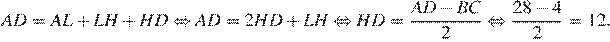
Ответ: 12.
Критерии проверки:
Ответ: 12
Источник: Банк заданий ФИПИ
Задание 24 № 311860
15.Основания трапеции равны 16 и 34. Найдите отрезок, соединяющий середины диагоналей трапеции.
Решение.
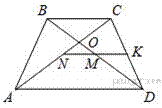
Пусть в трапеции ABCD с основаниями BC = 16 и AD = 34. Обозначим середину диагоналиAC через N, середину диагонали BD через M, а середину стороны CD через K.
ТогдаNK — средняя линия треугольника ACD, MK — средняя линия треугольника BCD. Значит, точки N, M и K лежат на одной прямой, и NM = NK − MK = 9.
Ответ: 9.
Критерии проверки:
Источник: МИОО: Диагностическая работа по математике 01.10.2013 вариант МА90106.
Задание 24 № 316359
16.Биссектриса угла A параллелограмма  пересекает его сторону
пересекает его сторону 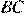 в точке
в точке 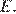 Найдите площадь параллелограмма
Найдите площадь параллелограмма 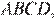 если
если 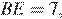
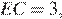 а
а 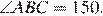
Решение.
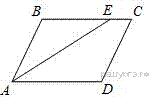
Накрест лежащие углы 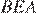 и
и 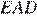 равны,
равны, 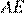 — биссектриса угла
— биссектриса угла 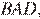 следовательно,
следовательно,
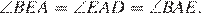
Значит, треугольник 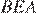 равнобедренный и
равнобедренный и 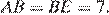
По формуле площади параллелограмма находим
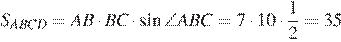
Ответ: 35.
Критерии проверки:
Источник: МИОО: Тренировочная работа по математике 19.02.2014 вариант МА90501.
Задание 24 № 333130
17.Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF = 24, BF = 10.
Решение.
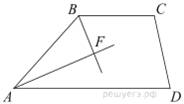
Сумма углов, прилежащих к боковой стороне трапеции, равна 180° , значит,
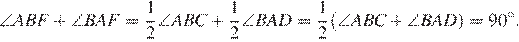
Получаем, что треугольник ABF прямоугольный с прямым углом F . По теореме Пифагора находим AB:
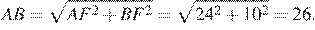
Ответ: 26.
Критерии проверки:
Источник: МИОО: Диагностическая работа по математике 17.04.2014 вариант МА90605
Задание 24 № 339403
18.Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC = 34.
Решение.
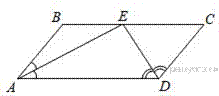 По определению параллелограмма
По определению параллелограмма 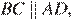
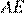 — секущая при параллельных прямых, следовательно, углы
— секущая при параллельных прямых, следовательно, углы 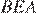 и
и 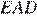 равны как накрест лежащие. Поскольку
равны как накрест лежащие. Поскольку 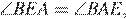 треугольник
треугольник 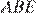 — равнобедренный, откуда
— равнобедренный, откуда 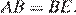 Аналогично, треугольник
Аналогично, треугольник 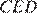 — равнобедренный и
— равнобедренный и 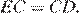 Стороны
Стороны 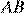 и
и 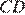 равны, как противоположные стороны параллелограмма, следовательно:
равны, как противоположные стороны параллелограмма, следовательно:
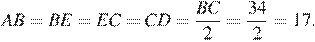
Ответ: 17.
Критерии проверки:
Задание 24 № 339709
19.Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC = 19, а расстояние от точки K до стороны AB равно 7.
Решение.
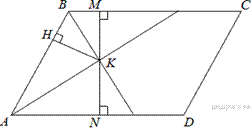 Проведём через точку пересечения биссектрис высоту. Введём обозначения как показано на рисунке. Рассмотрим треугольники
Проведём через точку пересечения биссектрис высоту. Введём обозначения как показано на рисунке. Рассмотрим треугольники 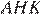 и
и 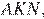 они прямоугольные, углы
они прямоугольные, углы 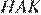 и
и 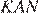 равны, сторона
равны, сторона 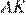 — общая, следовательно, треугольники равны, откуда
— общая, следовательно, треугольники равны, откуда 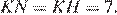 Аналогично, равны треугольники
Аналогично, равны треугольники 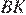 H и
H и 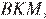 откуда
откуда 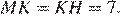 Найдём площадь параллелограмма как произведение основания на высоту:
Найдём площадь параллелограмма как произведение основания на высоту:
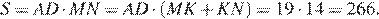
Ответ: 266.
Критерии проверки:
Задание 24 № 339619
20.Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
Решение.
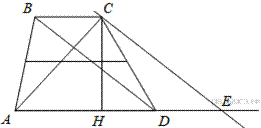 Пусть
Пусть 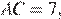
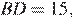
 — длина средней линии. Проведём высоту
— длина средней линии. Проведём высоту 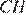 и проведём прямую
и проведём прямую 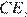 параллельную
параллельную 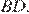 Рассмотрим четырёхугольник
Рассмотрим четырёхугольник 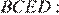
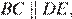
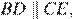 следовательно,
следовательно, 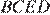 — параллелограмм, откуда
— параллелограмм, откуда 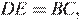
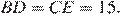 Рассмотрим треугольник
Рассмотрим треугольник 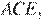
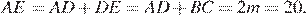 Пусть
Пусть 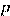 — полупериметр треугольника
— полупериметр треугольника 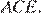 Найдём площадь треугольника
Найдём площадь треугольника 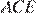 по формуле Герона:
по формуле Герона:
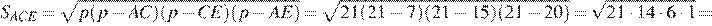
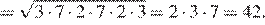
Выразим площадь треугольника 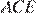 как произведение основания
как произведение основания  на высоту
на высоту 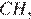 откуда найдём
откуда найдём 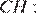
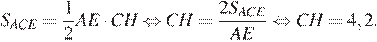
Площадь трапеции равна произведению высоты на полусумму длин оснований: 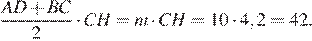
Ответ: 42.
Критерии проверки:
Задание 24 № 351992
21.Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 150°, а CD = 33.
Решение.
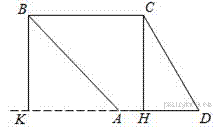
Введём обозначения как показано на рисунке. Проведём высоты 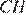 и
и 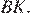 В трапеции сумма смежных углов при боковой стороне равна 180°, поэтому
В трапеции сумма смежных углов при боковой стороне равна 180°, поэтому 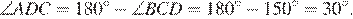 Из прямоугольного треугольника
Из прямоугольного треугольника 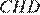 найдём сторону
найдём сторону 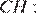
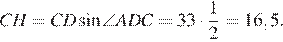
Углы  и
и 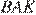 равны как накрест лежащие углы при параллельных прямых. Высоты
равны как накрест лежащие углы при параллельных прямых. Высоты 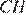 и
и 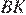 равны. Из прямоугольного треугольника
равны. Из прямоугольного треугольника 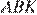 найдём
найдём 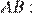
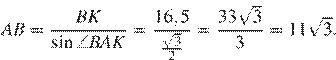
Ответ: 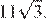
Источник: Банк заданий ФИПИ
Задание 24 № 352568
22.Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF = 20, BF = 15.
Решение.

Сумма углов, прилежащих к боковой стороне трапеции, равна 180° , значит,
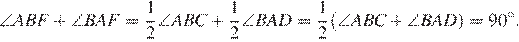
Получаем, что треугольник ABF прямоугольный с прямым углом F . По теореме Пифагора находим AB:
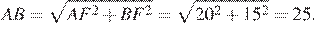
Ответ: 25.
Ответ: 25
Задание 24 № 353511
23.Найдите площадь трапеции, диагонали которой равны 16 и 12, а средняя линия равна 10.
Окружности
Задание 24 № 311650
1.В треугольнике  угол
угол 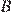 равен 72°, угол
равен 72°, угол  равен 63°,
равен 63°, 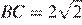 . Найдите радиус описанной около этого треугольника окружности.
. Найдите радиус описанной около этого треугольника окружности.
Решение.
Угол 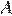 треугольника
треугольника  равен
равен 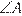 = 180° −
= 180° − 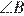 −
− 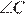 = 45°.
= 45°.
Радиус описанной окружности равен 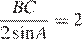 .
.
Ответ: 2.
Критерии проверки:
Источник: ГИА-2013. Математика. Пробные варианты от ФИПИ (1 вар.)
Задание 24 № 340853
2.Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 15, AC = 25.
Решение.
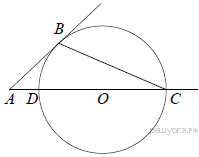 Пусть DC = x. Тогда по свойству касательной и секущей, проведённых из одной точки к окружности, получаем:
Пусть DC = x. Тогда по свойству касательной и секущей, проведённых из одной точки к окружности, получаем:
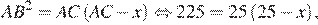 откуда
откуда 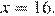
Ответ: 16.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 26.11.2014 вариант МА90201.
Задание 24 № 340879
3.Окружность, вписанная в треугольник ABC , касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 49°, 69° и 62°.
Решение.
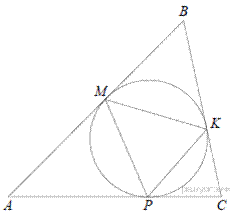 Пусть
Пусть
∠BAC = α , ∠ABC = β , ∠ACB = γ;
∠PKM = 49°, ∠MPK = 69°, ∠KMP = 62°.
По свойству касательных AM = AP, BM = BK , CP = CK . Значит, треугольники AMP, BMK и CPK равнобедренные, откуда получаем:
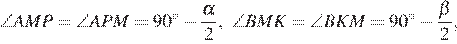
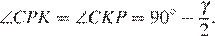
Значит, 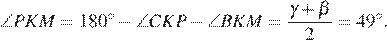 Аналогично получаем, что
Аналогично получаем, что 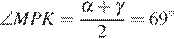 и
и 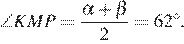
Решая систему относительно α , β и γ , получаем, что углы треугольника ABC равны 82°, 42°, 56°.
Ответ: 82°, 42°, 56°.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 26.11.2014 вариант МА90202.
Задание 24 № 339492
4.Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK = 18, а сторона AC в 1,2 раза больше стороны BC.
