Видимость треугольников на горизонтальной плоскости проекций

Проведём горизонтально проецирующую прямую, пересекающую стороны AC и DE данных треугольников. Эта проецирующая прямая пересекает DE в точке 5, а AB – в точке 6. Точка 5∈AB дальше отстоит от плоскости проекции Π1чем точка 6∈AB. Следовательно, сторона DEв Π1 полностью видима, а сторона AB на участке 61−M1 невидима. Этого достаточно для определения видимости в Π1, остальных сторон треугольников.

Видимость треугольников на фронтальной плоскости проекций

Проведём фронтально проецирующую прямую, пересекающую стороны EF и AC. Точка 4стороны F конкурирует с точкой 7 стороны AC. Точка 4 более удалена от плоскости проекций Π2, чем точка 7, и находится ближе к наблюдателю. Поэтому фронтальная проекция E2F2 полностью видима, а сторона A2C2 на участке N2−72 не видима. Этого достаточно для определения видимости треугольников во фронтальной плоскости проекций.

Прямые и плоскости, параллельные плоскости

Прямая параллельна плоскости, если вэтой плоскости имеется прямая, параллельная ей.

Пример

Через точку A провести отрезок прямой DE, параллельный горизонтали △ABC.

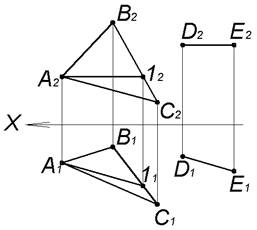
Из вершины A в плоскости треугольника ABC проведем горизонталь A−1.Фронтальная проекция отрезка D2E2 параллельна оси OX.

Горизонтальная проекция отрезка D1E1 параллельна горизонтальной проекции горизонтали A111.

Две плоскости взаимно параллельны, еслидве пересекающиеся прямые одной плоскости, параллельны двум пересекающимся прямым другойплоскости. У параллельных плоскостей одноименные главные их линии параллельны.

Пример

Через точку A провести плоскость β, параллельную плоскости α, заданной следами.

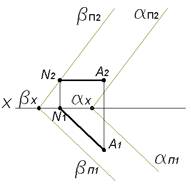
Чтобы построить плоскость, содержащую точку A и параллельную плоскости α, через точку A проведем одну из главных линий плоскости α например, горизонталь AN, параллельную плоскости α. Через фронтальный след горизонтали, точку N, проходит фронтальный след плоскости β, βΠ2∥αΠ2 Горизонтальный след βΠ2∥αΠ1 проходит через точку схода следов βX=βΠ2∩OX.

Прямые и плоскости, перпендикулярные плоскости

Прямая перпендикулярна плоскости,если она перпендикулярна любым двум пересекающимся прямым этой плоскости.

Чтобы построить проекции прямой, перпендикулярной плоскости, необходимо воспользоваться теоремой о проекциях прямого угла. Прямая перпендикулярна плоскости, если ее проекции перпендикулярны одноименным проекциям горизонтали и фронтали плоскости.

Пример. Провести через точку A плоскость, перпендикулярную заданной прямой m. Плоскость αзадать пересекающимися прямыми.

Через точку A проведем горизонталь h и фронталь f таким образом, чтобы они были перпендикулярны прямой m.

h1⊥m1∧f2⊥m2

Пример

Через точку A провести плоскость α, перпендикулярную прямой m. Плоскость α задать следами.

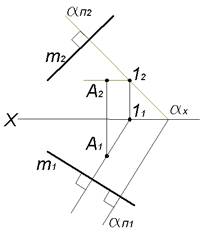
Через точку A проведем горизонталь A−1 перпендикулярно прямой

A2−12∥OX, (A1−11)⊥m1

Через фронтальный след 12 горизонтали A−1 проведем перпендикулярно прямой mфронтальный след αΠ2 плоскости. Горизонтальны след αΠ1 плоскости α проходит через точку схода следов плоскости α перпендикулярно горизонтальной проекции прямой m

αΠ1⊥m1

Пример

Восставить перпендикуляр к плоскости α в данной ее точке K.

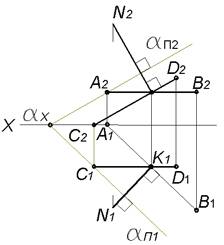
В плоскости α проведем горизонталь AB и фронталь CD. Проекции перпендикуляра к плоскости составляют прямые углы с одноименными проекциями горизонтали и фронтали плоскости α.

K1N1⊥A1B1∧K2N2⊥C2D2, K1N1⊥αΠ1∧K2N2⊥αΠ2

Прямая KN перпендикулярна любым прямым этой плоскости.