Вычерчивание прямых, острых, тупых углов

Прежде чем приступить к обучению школьников вычерчиванию острых и тупых углов, следует вернуться к построению прямого угла. До сих пор дети произвольно выбирали место чертежа. Теперь задается точка — вершина угла, или прямая, по которой должна пойти сторона будущего угла, или прямая и точка, ей принадлежа­щая. Эффективность работы учащихся будет во многом зависеть от того, с какой точностью они будут повторять за учителем приемы работы с чертежным треугольником. Учитель показывает и расска­зывает, как построить угол, вершина которого совпадает с данной точкой, а сторона принадлежит данной прямой. Учитель объясняет и показывает, что чертежный треугольник надо положить так, чтобы вершина его прямого угла совпала с заданной точкой, а сторона прямого угла совпала с заданной прямой. Вычерчивая прямые углы, учащиеся не только должны точно воспроизводить приемы работы с чертежным треугольником, которые показал учитель, но и сопровождать свои действия комментарием. После этого вы­черчиваются острые и тупые углы как произвольные, так и с вер­шиной в данной точке; со стороной, расположенной на данной прямой.

Соответствие построенного угла требуемому в задании обяза­тельно проверяется с помощью прозрачного чертежного треуголь­ника. Надо выработать у детей привычку вид каждого угла прове­рять с помощью чертежного треугольника.

Учащиеся учатся сравнивать углы по величине путем наложе­ния. Учитель спрашивает: «Какой из данных двух углов больше по величине?» или «Величина какого угла больше (меньше)?».

Учеников надо учить сравнивать величину двух острых углов, двух тупых углов, острого и тупого углов. Прием наложения углов ничем не отличается от приема наложения прямого угла чертежного треугольника на данный угол.

Далее учитель показывает, что величина угла не зависит от длины сторон на чертеже. С этой целью с учащимися рассматри­вается угол, определяется его вид. Затем учитель предлагает учени­кам продолжить стороны угла. Длина сторон на чертеже увеличи­лась, а величина угла не изменилась. Сравниваются чертежи прямых углов с различной длиной сторон. «Величина углов одинаковая,

а длина сторон разная»,— говорят ученики. Учитель спрашивает: «Зависит ли величина угла от длины сторон угла на чертеже?» С помощью чертежного треугольника дети устанавливают, что все прямые углы равны между собой, несмотря на то что у них может быть на чертеже разная длина сторон.

Основной задачей изучения углов в III классе является форми­рование у учащихся умения выделять углы в многоугольниках, умения определять их виды. На первых порах, когда учащимся еще трудно выделить угол многоугольника, его элементы (и ту часть плоскости, которая относится к нему), можно на таблицах, чертежах закрывать всю фигуру, оставляя лишь вершину и часть угла. После небольшой тренировки учащиеся смогут довольно легко «на глаз» определять виды углов многоугольника. Теперь учитель должен лишь проследить, умеют ли они проверять это с помощью чертежного треугольника.

Учащимся полезно предложить индивидуальные карточки, на которых изображены чертежи различных углов или многоуголь­ников. Школьники сначала «на глаз», а затем с помощью чертеж­ного треугольника определяют вид углов и подписывают их название или записывают номера углов в нужную колонку:

Название многоугольника	Номера острых углов	Номера прямых углов	Номера тупых углов

В V классе учитель знакомит учащихся с обозначением угла тремя заглавными буквами и чтением его. Учитель сообщает, что буква, обозначающая вершину, пишется в середине. Слово «угол» обозначается знаком 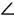, например: .АВС или CBA. Здесь В — вершина. ВА и ВС — стороны угла.

Углы могут быть обозначены и одной буквой: A, B, C — или цифрой: 1, 2, 3.

Учащимся предлагается выполнить следующие задания: 1) по­строить угол определенного вида и обозначить его буквами; 2) по­строить угол такого же вида, как на чертеже; 3) построить угол, больший или меньший прямого; 4) построить угол с вершиной в заданной точке; 5) построить угол, одна сторона которого принадле­жит данной прямой; 6) построить угол с вершиной в точке, принад­лежащей прямой, так, чтобы его сторона совпадала с данной пря­мой; 7) построить прямой угол так, чтобы одна его сторона при­надлежала прямой, а другая проходила через данную точку вне данной прямой.

Все эти упражнения выполняются сначала под руководством учителя (одновременно на доске и в тетрадях), затем детьми самостоятельно.

В VI классе при изучении пересекающихся прямых учащимся

приходится определять вид образующихся при этом углов, чтобы установить, являются ли эти прямые взаимно перпендикулярными. Наряду с обязательными упражнениями по этой теме наиболее подготовленным ученикам можно предложить рассмотреть чертеж с двумя парами пересекающихся прямых — перпендикулярных и не­перпендикулярных одна к другой — и определить виды углов, полу­ченных при пересечении. Чертеж, выполненный на прозрачной бу­маге, позволит учащимся путем перегибания листа бумаги наложить углы один на другой и сравнить их по величине.

С помощью углов с подвижными сторонами учитель знакомит учащихся с развернутым, а затем и полным углами. На примере углов, полученных при пересечении двух прямых, он показывает, что все полученные четыре угла составляют полный угол. В случае перпендикулярных прямых следует подчеркнуть, что полный угол будет равен четырем прямым углам, а сторона одного угла служит продолжением стороны другого угла. Развернутый угол равен двум прямым углам. У развернутого угла стороны расположены на одной прямой.

В VII классе хорошо успевающих учащихся можно познакомить с делением угла на две равные части (сверх программы), т. е. с биссектрисой угла. С этой целью учащимся предлагается на прозрачной бумаге начертить произвольный угол. Затем они перегибают чертеж так, чтобы стороны угла совпали, угол при этом делится линией сгиба пополам. Прямая чертится по линейке, начиная от вершины, учитель называет ее биссектрисой. Дети устанавливают, Что биссектриса — это луч с началом в вершине угла, делящий дан­ный угол пополам.

Когда школьники запомнят новое слово и научатся делить угол ни 2 равные части перегибанием листа бумаги, учитель знакомит их с построением биссектрисы с помощью циркуля.

Последовательность построения: 1) вычерчивается угол; 2) произвольным радиусом с центром в вершине угла проводится дуга, пересекающая стороны угла; 3) точки пересечения дуги со сторонами угла принимаются за центры новых дуг, которые проводятся одним и тем же радиусом до пересечения друг с другом; 4) от вершины угла через точку пересечения дуг проводится луч, он и является биссектрисой угла. Если чертеж выполнен на прозрачной бумаге, это легко проверить перегибанием чертежа.

После знакомства с измерением углов с помощью транспортира учащиеся проверяют правильность построения биссектрисы измере­нием полученных углов и сравнением их по величине.

В VII классе учащиеся повторяют виды углов, сравнивают их, классифицируют.

Учитель сообщает, что для измерения углов существует особая единица измерения — угловой градус. Ее можно получить, если прямой угол разделить на 90 одинаковых углов. Каждый угол равен 1 градусу и обозначается так: 1°. У учителя непременно должна быть таблица,, на которой изображен прямой угол, разделен­ный на 90 равных частей. Учащиеся сами должны назвать градусную

меру развернутого и полного углов, рассуждая так: «Развернутый угол равен двум прямым углам, значит, он содержит 180°, полный угол равен четырем прямым углам, значит, он равен 360°».

Здесь же рассматриваются величины острых и тупых углов. С этой целью учитель совмещает угол со сторонами прямого угла, разделенного на 90°, показывая учащимся, что острый угол меньше прямого, т. е. меньше 90°, а тупой больше прямого, т. е. больше 90° (но меньше развернутого). Затем даются упражнения, в ко­торых учащиеся по величине угла, выраженной в градусах, опре­деляют его вид.

В это же время необходимо школьников знакомить с устрой­ством транспортира и приемами построения и измерения углов с его помощью.

Учитель объясняет устройство транспортира: каждая из двух дуг транспортира представляет собой полуокружность, центр окруж­ности является центром транспортира, в основании транспортира находится линейка с делениями. Полуокружность транспортира раз­делена на 180°, на ней нанесены (по ходу и против хода часовой стрелки) штрихи от 0 до 180°. Один нулевой штрих находится от центра транспортира справа, другой — слева.