Пересечение прямой с плоскостью общего положения

Точку пересечения прямой с плоскостью общего положения строят в следующем порядке (способ вспомогательных секущих плоскостей, плоскостей посредников):

1) через заданную прямую проводят вспомогательную (проецирующую) плоскость;

2) строят линию пересечения вспомогательной плоскости с заданной;

3) находят положение точки пересечения прямых – данной и построенной линии пересечения.

На рисунке 12 показано построение точки пересечения прямой MN с плоскостью, заданной треугольником АВС.

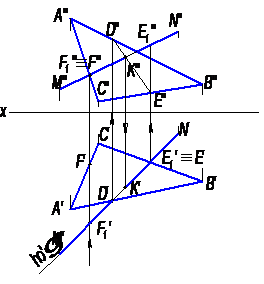
Рис. 12

Прямую MN заключили во вспомогательную горизонтально-проецирующую плоскость γ, которая задана только одним следом - h_оγ, проходящим через M′N′. Плоскость γ пересекает ∆ АВС по прямой DE. Линия пересечения DE и заданная прямая MN расположены в одной плоскости – γ и они пересекаются, что видно из их фронтальных проекций, в точке К, которая является общей для заданных прямой и треугольника. Т.е. будет определена фронтальная проекция К′′ точки пересечения К прямой MN с треугольником АВС. Горизонтальная проекция К′ определяется по ее фронтальной проекции с помощью линии связи.

Считая, что в пространстве ∆ АВС непрозрачный, необходимо определить видимые и невидимые части прямой MN относительно плоскости треугольника.

Видимость прямой MN в проекциях определена с помощью горизонтально- конкурирующих точек Е и Е₁ и фронтально-конкурирующих точек F и F₁. Границей видимости является точка К.

Из расположения фронтальных проекций E′′ и E₁′′ видно, что точка Е₁, принадлежащая прямой MN находится выше, чем точка Е, расположенная на стороне ВС ∆ АВС, а это значит, что горизонтальная проекция N′K будет видимой, а отрезок K′D′ будет невидимым (уйдет под треугольник).

Из расположения горизонтальных проекций F₁′ и F′ видно, что точка F₁, принадлежащая прямой MN, расположена к наблюдателю ближе, чем точка F, расположенная на стороне АС ∆ АВС. Значит фронтальная проекция M′′K′′ будет видимой, а участок от точки К′′ и до фронтальной проекции – А′′B′′ невидимый (оказывается за треугольником).

Пересечение плоскостей.

Пересечение двух плоскостей, одна из которых частного положения

Прямая линия, получаемая при взаимном пересечении двух плоскостей, вполне определяется двумя точками, каждая из которых принадлежит обеим плоскостям или одной точкой, принадлежащей двум плоскостям, и известным направлением линии пересечения.

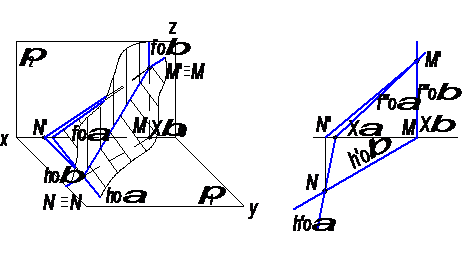
Рис. 13

На рисунке 13 показано построение линии пересечения MN плоскостей α и β. Плоскость β – горизонтально-проецирующая, плоскость α – общего положения. На наглядном изображении и на проекционном чертеже мы видим, что горизонтальная проекция линии пересечения – М′N′ расположена на h_оβ, т.к. плоскость β _┴ π₁. При этом точки M и N принадлежат обеим плоскостям, т.к. являются точками пересечения их одноименных следов.

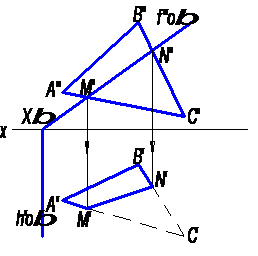
Рис. 14

На рисунке 14 показано построение линии пересечения MN двух плоскостей α (∆ АВС) и β. Плоскость α (∆ АВС) – общего положения, плоскость β – фронтально проецирующая. На фронтальной проекции, на пересечении сторон ∆ АВС с фронтальным следом плоскости β находим фронтальные проекции концов линии пересечения - М′′ и N′′. По фронтальным проекциям точек M и N с помощью линий связи определяются их горизонтальные проекции.

На рисунке 15 рассмотрен пример построения линии пересечения h плоскостей α и β, где α – горизонтальная плоскость, а плоскость β – общего положения.

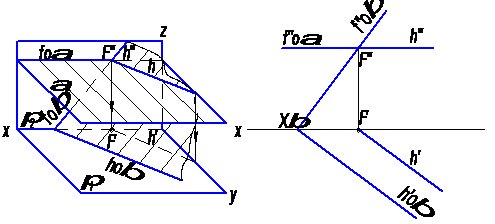
Рис. 15

Т.к. α – горизонтальная плоскость, то направление линии пересечения известно, h – горизонтальная прямая. Для построения ее проекций на чертеже достаточно знать одну общую точку. В данном примере это точка пересечения фронтальных следов – (·)F.