Горизонтально – проецирующая прямая

Прямая, параллельная плоскостям π₂ и π₃, т.е. перпендикулярная к π₁, называется горизонтально-проецирующей. На рисунках 13 изображен отрезок прямой MN_┴π₁.

Рис. 13

У горизонтально - проецирующей прямой проекция на горизонтальную плоскость проекций представит собой точку. На фронтальную и профильную плоскости проекций она спроецируется в отрезки прямых, параллельных между собой и равных по длине самому отрезку (M″N″≡ M″′N″′=[MN]).

Фронтально - проецирующая прямая

Прямая, параллельная плоскостям π₁ и π₃, т.е. перпендикулярная к π₂, называется фронтально-проецирующей. На рисунках 14 изображен отрезок прямой KL_┴π₂.

Рис.14

У фронтально-проецирующей прямой проекцией на фронтальную плоскость будет являться точка. На горизонтальную и профильную плоскости проекций она спроецируется в отрезки, равные по длине самому отрезку прямой (K′ L′ = K′′′ L′′′ = [KL]).

Профильно - проецирующая прямая

Прямая, параллельная плоскостям π₁ и π₂, т.е. перпендикулярная к π₃, называется профильно–проецирующей. На рисунках 15 изображен отрезок прямой GF_┴π₃.

Рис. 15

У профильно-проецирующей прямой проекция на профильную плоскость проекций представит собой точку. На горизонтальную и фронтальную плоскости она спроецируется в отрезки прямых, параллельных между собой и равных по длине самому отрезку (G′F′=G′′F′′=[GF]).

Прямые, параллельные двум плоскостям проекций и перпендикулярные к третьей называются проецирующими.

Прямые уровня и проецирующие называют прямыми частного положения.

Прямая общего положения

Прямая, непараллельная ни к одной из плоскостей проекций, называется прямой общего положения. На рисунках 16 изображен отрезок прямой ВС – общего положения.

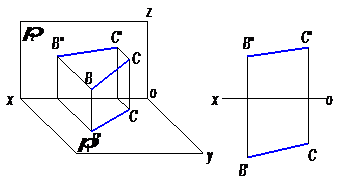
Рис. 16

У прямой общего положения ни одна из проекций не параллельна оси проекций и не перпендикулярна к ней. Каждая из проекций меньше самого отрезка, (В′С′<ВС, В′′С′′<ВС, В′′′С′′′<ВС.

Плоскость на чертеже. Классификация плоскостей.

Способы задания плоскости на эпюре.

Плоскость на эпюре может быть задана:

а) тремя точками, не лежащими на одной прямой линии (рис. 17);

Рис. 17

б) прямой линией и точкой взятой вне прямой (рис. 18);

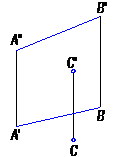
Рис. 18

в) двумя пересекающимися прямыми (рис. 19);

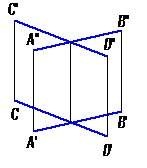
Рис. 19

г) двумя параллельными прямыми (рис. 20);

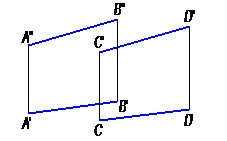
Рис. 20

д) проекциями любой плоской фигуры - треугольника, квадрата, окружности (рис. 21), собственно это вариант способа задания плоскости пересекающимися прямыми, а задание плоскости треугольником вытекает из способа её задания тремя точками;

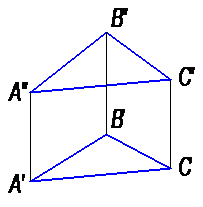
Рис. 21

е) плоскость может быть изображена на эпюре при помощи прямых, по которым она пересекает плоскости проекций, т.е. следами (рис. 22).

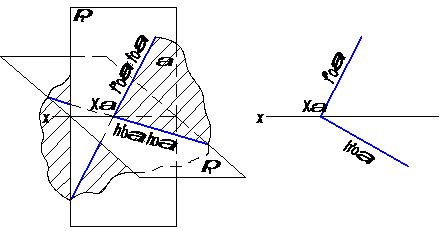
Рис. 22

Прямые, по которым некоторая плоскость пересекает плоскости проекций, называются следами этой плоскости на плоскостях проекций или короче следами плоскости.

На рисунке 22 изображена плоскость α пересекающая горизонтальную плоскость проекций по прямой, обозначаемой h_oα и фронтальную плоскость по прямой, обозначаемой ƒ_оα.

Прямая h_oα называется горизонтальным следом плоскости, прямая ƒ_оα – фронтальным следом плоскости α.

Точка пересечения плоскости α с осью проекций х (точка пересечения следов плоскости) называется точкой схода следов, обозначена х_α.

След плоскости на плоскости проекций сливается со своей проекцией на этой плоскости. Так горизонтальный след плоскости α сливается со своей горизонтальной проекцией (h′_оα≡h_oα), фронтальная проекция этого следа (h′′_оα) располагается на оси проекций х.

Фронтальный след плоскости α сливается со своей фронтальной проекцией (f′′_oα≡f_oα), горизонтальная проекция этого следа (f′_оα) располагается на оси проекций х.

На чертеже плоскость может быть задана следами (рис. 22). Такой чертеж нагляден и удобен для построений.

Угол, образованный между следами на чертеже не равен углу, образованному следами плоскости в пространстве.

Положения плоскости

Плоскость, как и прямая линия, относительно плоскостей проекций может занимать семь положений.

Плоскости общего положения.

Такие плоскости не перпендикулярны ни к одной из плоскостей проекций. Следы плоскостей общего положения никогда не перпендикулярны к осям проекций. На рисунке 22 дан пример плоскости общего положения.

2) Плоскости, перпендикулярные двум плоскостям проекций (возможны три случая):

а) горизонтальная плоскость (рис. 23);

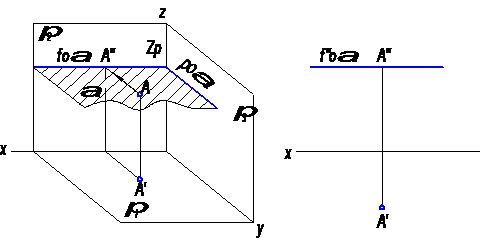
Рис.23

На рисунке 23 плоскость α║π₁, т.е. α _┴ π₂ и π₃.

Фронтальная проекция точки А, лежащей в плоскости α, будет расположена на фронтальном следе этой плоскости.

б) фронтальная плоскость (рис. 24);

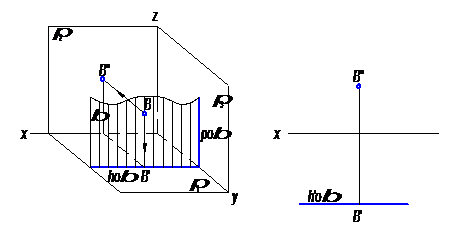
Рис.24

На рисунке 24 плоскость β║π₂, т.е. β _┴ π₁ и π₃.

Горизонтальная проекция точки В, лежащей в плоскости β, будет расположена на горизонтальном следе плоскости

в) профильная плоскость(рис. 25);

Рис. 25

На рисунке 25 плоскость α║π₃, т.е. α _┴ π₁ и π₂.

Горизонтальная проекция точки С, лежащей в плоскости α, будет расположена на горизонтальном следе этой плоскости, фронтальная проекция точки С – на фронтальном следе плоскости α.

3) Плоскости, перпендикулярные одной плоскости проекций (возможны так же три случая):

а) горизонтально – проецирующая плоскость(рис. 26);

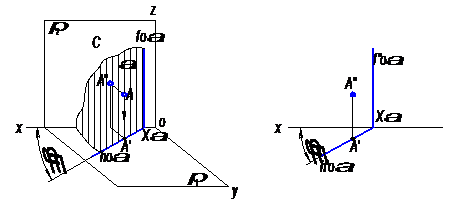
Рис.26

На рисунке 26 плоскость α _┴ π₁. Фронтальный след перпендикулярен к плоскости π₁ и к оси проекций х. Горизонтальный же след составляет с осью проекций не прямой угол, равный углу между горизонтально – проецирующей плоскостью и плоскостью проекций π₂.

б) фронтально – проецирующая плоскость (рис. 27);

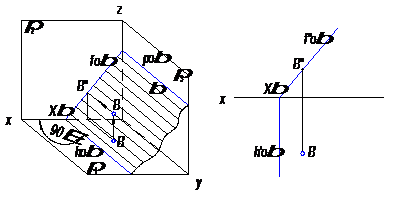
Рис. 27

На рисунке 27 плоскость β _┴ π₂. Горизонтальный след перпендикулярен к плоскости π₂ и к оси проекций х. Фронтальный след составляет с осью проекций не прямой угол, равный углу между фронтально – проецирующей плоскостью и плоскостью π₁.

в) профильно – проецирующая плоскость (рис. 28);

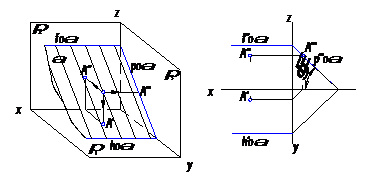
Рис. 28

На рисунке 28 дана плоскость α _┴ π₃.

Горизонтальный и фронтальный следы этой плоскости параллельны оси х и, следовательно, параллельны между собой. Угол γ^о – это угол, который образует профильно – проецирующая плоскость α с горизонтальной плоскостью проекций.

Главные линии плоскости

К числу прямых, занимающих особое положение в плоскости, относят горизонтали, фронтали, профильные прямые и линии наибольшего наклона к плоскостям проекций

Горизонталями плоскости называются прямые, лежащие в ней и параллельные горизонтальной плоскости проекций Горизонтали принято обозначать на чертежах буквой h (рис. 29).

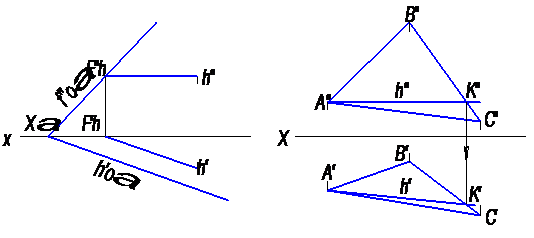
Рис. 29

На рисунке 29 построены горизонтали плоскостей α и β (∆АВС).

Т. к. горизонталь плоскости есть прямая, параллельная плоскости π₁, то фронтальную проекцию h′′ строят параллельно оси х. Плоскость α на рисунке 29 задана следами и горизонтальный след этой плоскости есть ее нулевая горизонталь. Горизонтальная проекция горизонтали h′ параллельна горизонтальному следу плоскости h_оα.

Построенная прямая АК на рисунке 29 является горизонталью плоскости β (∆АВС); эта прямая лежит в плоскости, так как проходит через две точки ей принадлежащие и параллельна плоскости π₁.

Фронталями плоскости называются прямые, лежащие в ней и параллельные плоскости проекций π₂.

Фронтали принято обозначать на чертежах буквой f (рис. 30).

Построение фронталей начинают с построения горизонтальной проекции – f ′.

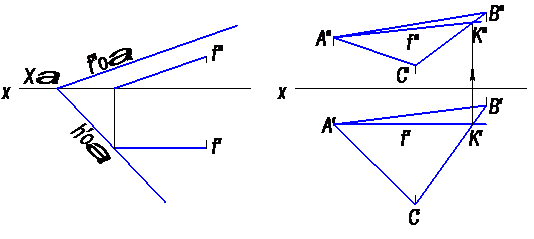
Рис. 30

Т. к. фронталь плоскости есть прямая параллельная плоскости π₂, то горизонтальную проекцию f ′ строят паралельно оси х. Фронтальный след плоскости α есть ее нулевая фронраль, поэтому фронтальная проекция фронтали – f ′′ (рис. 30) параллельна фронтальному следу плоскости – f_оα.

Построенная на рисунке 30 прямая AК является фронталью плоскости ∆АВС; эта прямая лежит в плоскости, т. к. проходит через точки А и К, принадлежащие ей, и параллельна плоскости π₂.