Определение точки встречи прямой и плоскости.

ПОСТРОЕНИЕ ТОЧКИ ВСТРЕЧИ ПРЯМОЙ С ПЛОСКОСТЬЮ

В пространстве прямая может либо принадлежать плоскости, либо не принадлежать плоскости. Это утверждение справедливо и для точки. Прямая принадлежит плоскости, если она проходит:

Через две точки, принадлежащие плоскости;

Через точку плоскости параллельно любой прямой этой плоскости.

Точка принадлежит плоскости, если она расположена на прямой (кривой), лежащей в данной плоскости.

Пусть нам дан ортогональный чертёж плоскости a - общего положения, заданной двумя пересекающимися прямыми а и b. Чтобы построить прямую, принадлежащую данной плоскости, необходимо выполнить одно из вышеперечисленных условий. На прямых a и b возьмём две точки А и В и проведём прямую f через эти точки. Прямая f принадлежит плоскости a, т. к. она проходит через две точки, принадлежащие данной плоскости.

Алгоритм определения точки пересечения прямой и плоскости:

Пусть плоскость задана параллельными прямыми n и m. Плоскость Сигма(n||m) l пересекает сигма в точке К. В плоскости задают прямую t, конкурирующую с данной прямой. Отмечают точки пересечения данной прямой и конкурирующей прямой. Видимость участков определяют при помощи конкурирующих точек.

Взаимное положение прямой и плоскости определяется количеством общих точек, принадлежащих прямой и плоскости. Прямая, имеющая с плоскостью одну общую точку, пересекает плоскость.

Нахождение точки пересечения прямой и плоскости является одной из основных задач начертательной геометрии. Эта задача, как вспомогательная, входит в решение более сложных задач на пересечение поверхностей плоскостью, на построение линии пересечения двух поверхностей и т.п.

В зависимости от положения прямой и плоскости относительно плоскостей проекций можно выделить три задачи на построение точки встречи прямой и плоскости:

- пересечение проецирующей плоскости с прямой общего положения;
- пересечение плоскости общего положения с проецирующей прямой;
- пересечение плоскости общего положений с прямой общего положения.

7.2.1.Построение точки встречи прямой общего положения с проецирующей плоскостью
Рис. 7.4.

В качестве примера построим точку встречи фронтально проецирующей плоскости с прямой общего положения n (рис.7.4). Пусть n = = М. М₂ - фронтальная проекция искомой точки М должна лежать на фронтальной проекции П₂ прямой n, как точка, принадлежащая прямой n. В то же время фронтальная проекция М₂ точки М должна лежать на следе ₂ плоскости , так как искомая точка принадлежит и плоскости . Следовательно, искомая фронтальная проекция М₂ точки М может лежать только на пересечении n₂ и ₂. Имея фронтальную проекцию М₂ точки М, при помощи линии связи легко найти ее горизонтальную проекцию.
7.2.2.Построение точки встечи плоскости общего положения с проецирующей прямой

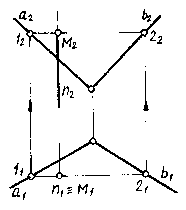
Рис. 7.5.

На рис.7.5 показано построение точки встречи горизонтально проецирующей прямой n с плоскостью общего положения (a b). Горизонтальные проекции всех точек, принадлежащих данной прямой, в том числе и горизонтальная проекция М₁ искомой точки М, будут совпадать с n₁ - горизонтальной проекцией прямой n. Следовательно, задача сводится к нахождению недостающей фронтальной проекцииМ₁ точки М, лежащей в плоскости . Через М₁ проведем прямую 1₁2₁. По линиям связи найдем фронтальные проекции 1₂, 2₂ точек 1 и 2, через которые проведем фронтальную проекцию прямой 12. На пересечении 1₂2₂ с n₂ и будет находиться фронтальная проекция М₂ точки М.
7.2.3.Построение точки встречи прямой общего положения с плоскостью общего положения
Пусть дана некоторая плоскость и прямая n (рис.7.6). Требуется построить точку М пересечения данных прямой и плоскости.
Решение этой задачи состоит из трех простейших последовательных операций:

1) через прямую проводят вспомогательную плоскость ;
2) находят линию пересечения 1 данной и вспомогательной плоскостей;
3) отмечают искомую точку М как точку пересечения прямой 1 с данной прямой n.

Пример построения точки встречи прямой общего положения с плоскостью общего положения на комплексном чертеже приведен на рис. 7.7. Заключаем прямую n в горизонтально проецирующую плоскость ( ₁ n₁). Находим линию пересечения плоскостей и ( =12). Горизонтальная проекция этой прямой совпадает с горизонтальной проекцией прямой n. Фронтальную проекцию прямой 12 проводим через 1₂ и 2₂, которые находим с помощью линий связи по принадлежности плоскости . Отмечаем точку пересечения фронтальных проекций 1₂2₂ и n₂ прямых 12 и n ( (1₂2₂ n₂ = M₂). M₂ является фронтальной проекцией точки встречи прямой n с плоскостью . Горизонтальную проекцию строим по линиям связи по принадлежности точки M прямой n.

Видимость прямой n определяем с помощью конкурирующих точек. Конкурирующими называют точки, проекции которых совпадают. Для определения видимости на П₁ в качестве конкурирующих возьмем точки 1 и 3, одна из которых принадлежит прямой ВС, вторая - n. Найдем фронтальные проекции этих точек. Так как точка 1 раположена выше точки 3, то на П₁ мы видим плоскость, а прямую n не видим. В точке пересечения видимость меняется на обратную. Видимость на П₂ находим с помощью конкурирующих точек 4 и 5 аналогично.

Другой способ:Алгоритм определения точки пересечения прямой и плоскости:

Пусть плоскость задана параллельными прямыми n и m. Плоскость Сигма(n||m) l пересекает сигма в точке К. В плоскости задают прямую t, конкурирующую с данной прямой. Отмечают точки пересечения данной прямой и конкурирующей прямой. Видимость участков определяют при помощи конкурирующих точек.