Расстояние от точки до прямой на плоскости

ЗАДАЧА. Доказать, что координаты проекции точки M*(x*,y*) на прямую l, заданную уравнением (29.5), можно найти по формулам (32.2).

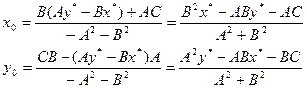(32.2)

Итак, расстояние от точки M*(x*,y*) до прямой l, задаётся уравнением (29.5), можно найти по формуле:

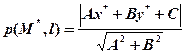(32.3)

Эллипс, как кривая второго порядка. Его полуоси, эксцентриситет, фокусы и директрисы. Окружность в качестве частного случая эллипса.

Эллипс, как кривая второго порядка.

Определение 33.2. Эллипсомназывается геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная.

отрезку (рис. 33.1).

Теорема 33.1.Пусть сумма расстояний от точки эллипса до фокусов равна 2a, а расстояние между фокусами –– 2c. Тогда в выбранной системе координат эллипс имеет уравнение

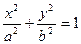(33.2)

где

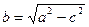(33.5)

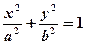(33.4)

Определение 33.3.Уравнение (33.4) называется каноническимуравнением эллипса.

Исследование формы эллипса. Его эксцентриситет, фокусы и директрисы.

Прежде, чем нарисовать эллипс, выясним некоторые его свойства.

Свойство 33.1. Эллипс обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых находятся его фокусы, и центром симметрии. Если эллипс задан каноническим уравнением (33.4), то его осями симметрии служат оси Ox и Oy, начало координат –– центр симметрии.

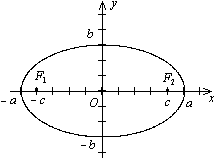
Определение 33.4. Точки пересечения эллипса с его осями симметрии называются вершинамиэллипса, центр симметрии –– центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины –– большой полуосью эллипса. Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины –– малой полуосью. Величина 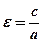называется эксцентриситетом эллипса.

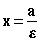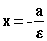Прямые и называются директрисами эллипса

Окружность, как частный случай эллипса

Общее уравнение окружности

Определение 33.5.Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центромокружности.

Получим уравнение окружности, если известны ее центр и радиус.

Теорема 33.2. Окружность радиуса R с центром в точке M₀ (x₀; y₀) имеет уравнение

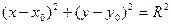(33.7)

Гипербола

Определение 34.1 Гиперболойназывается геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусамигиперболы, есть величина постоянная.

Теорема 34.1. Пусть расстояние между фокусами F₁ и F₂ гиперболы равно 2c, а абсолютная величина разности расстояний от точки гиперболы до фокусов равна 2a. Тогда гипербола в выбранной выше системе координат имеет уравнение

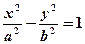(34.1)

где

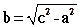(34.2)

Определение 34.2 Уравнение (34.1) называется каноническимуравнением гиперболы.

Свойство 34.1. Гипербола обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых лежат фокусы гиперболы, и центром симметрии. Если гипербола задана каноническим уравнением, то ее осями симметрии служат координатные оси Ox и Oy, а начало координат –– центр симметрии гиперболы.

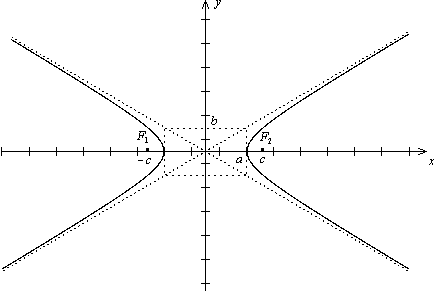
Определение 34.3. Точки пересечения гиперболы, заданной каноническим уравнением (34.1), с осью Ox называются вершинами гиперболы, отрезок между ними называется действительнойосью гиперболы. Отрезок оси ординат между точками (0; -b) и (0; b) называется мнимой осью. Числа a и b называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром. Величина 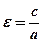называется эксцентриситетом гиперболы.

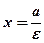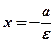Прямые и называются директрисамигиперболы, а прямые 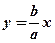и 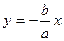- ее асимптотами (ранее было показано, что эти прямые будут асимптотами и согласно определениям математического анализа). Прямоугольник, диагоналями которого являются асимптоты гиперболы, а пара его параллельных сторон проходят через ее вершины, называется основным прямоугольником гиперболы (Тогда оси гиперболы параллельны сторонам ее основного прямоугольника).

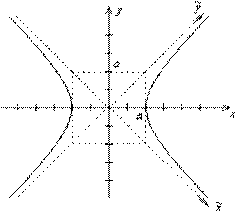
Рис. 33.4.Равносторонняя гипербола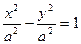

Парабола

Определение 34.4.Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.

Теорема 34.2. Пусть расстояние между фокусом F и директрисой l параболы равно p. Тогда в выбранной системе координат парабола имеет уравнение

y2=2px

(34.3)

Определение 34.5. Уравнение (34.3) называется каноническим уравнением параболы.

Свойство 34.2. Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью Ox.

Доказательство. Проводится аналогично доказательству свойства 33.1 для эллипса.

Определение 34.6. Точка пересечения оси симметрии с параболой называется вершиной параболы. Эксцентриситетом параболы (по определению) является число ε=1

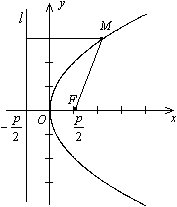
Рис.34.6.Парабола