Серия 12, наверное. Послеканикулярная

1. Расставьте числа 1 и -1 в клетки доски 5x5 так, чтобы во всех строчках, кроме последней, сумма была положительна, а во всех столбцах, кроме последнего, сумма была отрицательна.

2. Сколько существует натуральных чисел, не больших миллиона, каждое из которых не является ни полным квадратом, ни полным кубом, ни точной четвёртой степенью?

3. Даны 4 последовательных натуральных числа. Вася перемножил наибольшее с наименьшим, а Коля - два средних. Докажите, что Васин результат на 2 меньше.

4. Какое максимальное количество клеток можно отметить на доске 6x6 так, чтобы в каждой Г-тетраминошке было не более одной отмеченной?

5. Палиндром - это такое слово или число, которое справа налево и слева направо читается одинаково (например, 12321). Существует ли 20-значное простое число-палиндром?

6. Есть 100 различных гирь. Доказать, что можно выбрать две из них, так чтобы к ним нельзя было добавить никакую гирю из оставшихся и установить с помощью этих трёх гирь равновесие на весах.

7. В фирме 1111 сотрудников. Каждый из них обязан отработать в году 7 дней подряд на уборке территории. Доказать, что найдется 7 дней в году (не обязательно идущих подряд), что на уборке в этот день работало нечётное число сотрудников.

Серия 13, начало.

1.

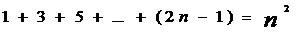
а) Докажите это с помощью индукции.

б) Докажите это с помощью геометрии.

2. В конференции участвовали 19 ученых. После конференции каждый из них отправил 2 или 4 письма участникам этой конференции. Могло ли получиться так, что каждый участник получил по 3 письма?

3. Количество интегралов, взятых Марией Михайловной, выражается трехзначным числом, начинающимся на 9. Если первую цифру этого числа перенести в конец, то получим количество интегралов, взятых Анной Михайловной. Известно, что Анна Михайловна взяла на 90 интегралов меньше. Выразите их мучения численно.

Серия 13, продолжение.

1. На какое минимальное количество прямоугольников можно разрезать следующую фигуру:
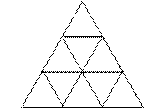2. Правильный треугольник разбит прямыми, параллельными сторонам, на 9 равных правильных треугольников. Петя отметил один из входящих в него треугольников невидимыми чернилами. Вася может указать любой треугольник со сторонами, идущими по линиям разбиения, и Петя скажет ему, лежит ли отмеченный треугольник в указанном. За какое наименьшее число таких вопросов Вася наверняка сможет найти отмеченный треугольник?
3. Вражеская шпионская сеть устроена следующим образом. Каждый из шпионов знает ровно четырех других. Получив какую-либо информацию шпион передает ее всем другим, известным ему, шпионам. Однажды, при передаче одного важного сообщения все шпионы сработали безукоризненно, кроме Васи, который не смог связаться со своим знакомым шпионом Петей. Докажите, что, несмотря на это вся сеть будет оповещена.
4. Все рыцари и лжецы острова построились по кругу, и каждый сказал, про соседа справа – рыцарь он или лжец. На основании этой информации, путешественник смог сообразить, какова доля рыцарей в населении. А чему она равна?

Серия 14. Жужжащая.

1. Максим должен был разделить число на 2, а к результату прибавить 3, а он, по ошибке, умножил число на 2, а от полученного произведения отнял 3. Ответ все равно получился правильный. Какой?

2. Артем и Саша вместе знают столько же плохих слов, сколько Игорь и Дима. А Артем с Димой знают таких слов больше, чем Саша с Игорем. Расположите юных лингвистов по количеству известных им плохих слов, если известно, что Саша знает их больше, чем Артем и Игорь вместе взятые.

3. В квадратном ковре со стороной 1 м моль проела 15 точечных дырок. Докажите, что из него можно вырезать неповрежденный круг радиуса 12,5 см.

4. На шестиугольной решетке (см. рисунок) пчёлы сложили мед в 300 шестиугольников. Докажите, что из них можно выбрать 100 так, чтобы не было соседних по стороне.

5. Выразите без многоточий число 1+2+4+…+2¹⁰⁰.

6. На клетчатой бумаге построены несколько прямоугольников со сторонами, параллельными линиям сетки и общим центром О в одном из узлов сетки. За один вопрос можно про любой из узлов узнать, у скольких прямоугольников он лежит внутри. Как за четыре вопроса узнать, сколько прямоугольников содержат только один узел О?

7. Есть n одинаковых банок. Из них n-1 доверху заполнены красками разных цветов, а последняя пустая. Разрешается переливать из любой банки в любую произвольное количество краски. Докажите, что можно сделать так что каждая из n банок будут заполнены поровну равномерной смесью всех красок.

Олипиада ЮМШ 6 класса 5. Есть доска 9×9 клеток. В каждую клетку поставили число 0, 1 или 2 так, чтобы в каждом квадратике 2×2 сумма была больше четырёх. Докажите, что сумма всех чисел на доске не меньше 89.6. Мама выдала Ванечке двузначное число. Ванечка сложил в столбик это число с ним же, после чего проделал то же самое с полученным результатом, и так 11 раз. Когда мама стала проверять его вычисления, выяснилось, что Ванечка при сложении двойки с двойкой получал всегда вместо четырёх пять (или шесть, если там был ещё перенос). В итоге у него получилось число, которое оканчивается ровно на один ноль. Каким могло быть исходное число?7. Круг разбит на 100 секторов. Мирза и Егор по очереди заполняют сектора (в произвольном порядке) натуральными числами (первым ходит Мирза). Когда все сектора заполнены, Мирза пишет на доску ещё одно натуральное число, после чего Егор режет круг на две половинки (по 50 секторов). Если сумма чисел в одной из них оканчивается на те же две цифры, что и число на доске, то побеждает Егор, иначе побеждает Мирза. Кто победит при правильной игре?

15 серия: Начало.

1. Диана, Кирилл и Афанасий задумали по трехзначному числу. Могло ли так оказаться, что сумма числа Афанасия с числом Дианы равна 600, а сумма числа Кирилла с числом Дианы равна 1500?

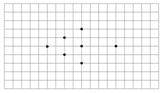
2. На клетчатой бумаге поставлено 7 точек так, как показано на рисунке. Перечеркните все эти точки тремя отрезками, не отрывая карандаша от бумаги. Отрезки не обязательно должны проходить по линиям сетки.

3. На математический кружок пришли три длинноволосых ребёнка. Их фамилии - Кубанец, Чиковани и Никитина, имена - Саша, Женя и Дима. Учитель знает об этом, но на взгляд не может определить, кто из них мальчик, а кто девочка. Каждый из детей назвал своё имя и фамилию, причём учителю известно, что мальчики называют и то и другое неверно, а девочки правильно. Может ли учитель гарантированно определить по ответам детей, сколько среди них мальчиков? (Кубанец и Чиковани могут быть как мальчиками, так и девочками, Саша и Женя тоже).

4. В куче лежит N камней, N>3. Двое играют в игру. Первый игрок забирает из кучи один камень. Каждым следующим ходом можно забрать либо ровно на один камень больше, либо ровно на один меньше, чем только что взял соперник, но не менее одного камня. Проигрывает тот, кто не может сделать очередной ход. Кто из игроков может выиграть, как бы ни играл его соперник?