Построение перспективы объекта

Заметим, что линии контура плана, представленного на рис. 28, могут быть разделены на два пучка I и II параллельных прямых, и определим перспективы несобственных точек (F₁ и F₂) каждого из пучков. При этом точка F₁ является перспективой бесконечно уда­ленной точки пучка параллельных прямых направления I, а точка F₂ - направления II. Эти точки определены с помощью проецирующих лу­чей SF₁ и SF₂ параллельных соответственно направлению I и II, которые пересекут картину в точках, лежащих на линии горизонта h-h.

В качестве вторых точек для построения перспективы линий контура плана использованы характерные точки, в которых эти линии пересекают плоскость картины (точки N⁰₀ …N⁴₀ на рис.28а).

Эти точки найдены в пересечении продолжений горизонтальных проекций прямых с горизонтальным следом (П')' плоскости картины и расположены на основании 0¹-0² картины.

Перенесем полученные точки F₁, F₂, N⁰₀ …N⁴₀ на плоскость картины (рис. 28б). Если перспектива строится без увеличения, то отрезки PF₁ и PF₂ на рис. 28б равны соответственно отрезкам p₀F'₁ и p₀F'₂ рис. 28а. Перенос точек N⁰₀ …N⁴₀ с эпюра (рис.28а) на картину (рис. 28б) можно осуществить с помощью полоски бумаги, которую следует приложить кромкой к следу (П')' картины и отметить на кромке точки N⁰₀ …N⁴₀ и p₀. Далее, эту полоску совмещаем с основанием 0¹-0² картины на рис. 28б, так, чтобы точка p₀ совпала с той же точкой на основании. Теперь остается построить перспек­тивы прямых, пересечение которых и определит вершины заданного контура. Так, перспектива точки 3 определится в пересечении перспектив прямых N²₀F₂ и N³₀F₁. Аналогично находят и другие точки. Следовательно, каждая точка плоской фигуры определяется пересечением прямых, принадлежащих двум разным пучкам параллель­ных линий.

Следует отметить, что в качестве второй точки для построе­ния перспективы прямых не обязательно брать их начала. Суще­ствуют и другие приемы (см., например, [I], § 72, с.153-154).

Закончив построение перспективы контура плана, сле­дует перейти к изображению самого предмета.

рис. 29

На рис. 29 приведены ортогональные проекции объекта, анало­гичного рассмотренному на рис. 21. Не повторяя объяснений, отно­сящихся к построению перспективы плана, опишем процесс создания перспективы объекта (рис. 30).

рис. 30

Отметим, что построение перспективы объекта в данном слу­чае проведено с увеличением всех линейных размеров на картине в 2 раза. Это значит, что расстояние между основанием картины и линией горизонта на рис. 30 в 2 раза больше чем на рис. 29. От­резки PF₁ и PF₂ рис. 30 в 2 раза больше отрезков p₀F₁ и p₀F₁ рис.29 и т.д.

Дальнейшие построения проводим в следующей последователь­ности.

1. Через все вершины вторичной проекции объекта (точки 1'...9') проводим вертикальные прямые.

2. От точки 1' на проходящей через нее вертикали откла­дываем отрезок 1'A' длиной 2Н₁; заметим, что ребро 1А распо­лагается в плоскости картины и, следовательно, изображается в натуральную величину, а масштаб изображения принят рав­ным 2:1.

3. Через точку A' проводим прямые в точки схода F₁ и F₂. На этих прямых с помощью вертикальных линий связи 2'-M' и 7'-C' находим соответственно точки M' и C'. Точка D' может быть най­дена при пересечении вертикальной линии связи 6'-D' либо с пря­мой C'F₁, либо с прямой M'F₂.

4. Для получения перспективы точек B'иI', через прямые 9'B' и 8'I' проводим вертикальную плоскость a (на рис. 30 по­казана перспектива горизонтального следа этой плоскости -a') и строим линию пересечения плоскости a с картиной П'-a∩П'. Затем, откладываем на этой линии от основания картины отрезок N³₀N'₃, равный H₂ (с учетом масштаба) и соединяем точку N'₃ с точкой схода F₁. Искомые точки B' и I' получаем в пересечении прямой N'₃F₁ с вертикальными линиями связи, проведенными через точки 9' и 8' соответственно.

5. Соединив точку I' с точками M' и D', а точку B' с точка­ми A' и C', получим перспективное изображение пятиугольной приз­мы.

6. Для построения перспективы вертикальных ребер высотой Н, проходящих через точки 3', 4', 5', 6', проводим построения логичные, изложенным в п. 4 и затем в п. 3 (здесь через ребро 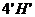проведена вертикальная плоскость ).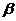