Две параллельные прямые и секущая, признаки параллельности прямых

Данный факт является очевидным, но необходимо рассмотреть более полезные утверждения, касающиеся такой системы объектов, как две параллельные прямые и секущая (прямая, пересекающая две параллельные прямые) (см. Рис. 5).

Рис. 5.

Две параллельные прямые и секущая

Если известно, что 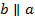, как на Рис. 5, то у указанных углов существуют специальные названия:

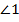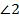и – накрест лежащие,

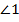и 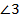– односторонние,

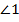и 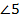– соответственные,

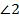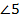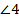и , и 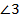– вертикальные.

Для соотношений между этими углами можно сформулировать ряд признаков параллельности двух прямых:

1. 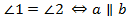– накрест лежащие углы равны тогда и только тогда, когда прямые параллельны.

2. 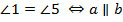– соответственные углы равны тогда и только тогда, когда прямые параллельны.

3. 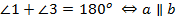– сумма односторонних углов равна 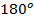тогда и только тогда, когда прямые параллельны.

Примечательно то, что указанные признаки параллельности можно применять и в обратном направлении и получать соотношения между углами при пересечении двух параллельных прямых секущей.

Знание этих фактов может помочь не только при решении геометрических задач, а при доказательстве важнейших теорем о треугольнике, которые мы сейчас и рассмотрим.

Теорема о сумме углов треугольника

Сумма внутренних углов в любом треугольнике равна 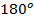(см. Рис. 6).

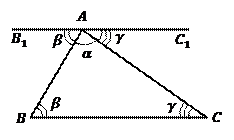
Рис. 6.

Теорема о сумме углов треугольника

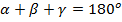или, в обозначениях латинских букв, .

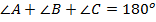Доказательство.

Проведем прямую .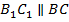

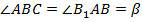как накрест лежащие, 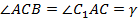как накрест лежащие.

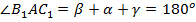как развернутый угол.

Доказано.

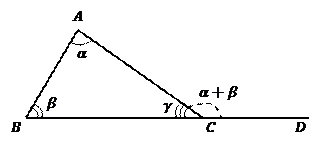
Рис. 7.

Теорема о внешнем угле треугольника

Теорема о внешнем угле треугольника

Любой внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

.

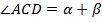Доказательство.

Сумма углов треугольника .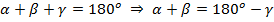

С другой стороны, 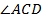находится с использованием смежного к нему угла : .

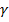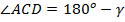Используя равенство, полученное выше, имеем: .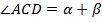

Доказано.

В качестве примера докажем еще один важный факт, который можно назвать еще одним признаком равенства треугольников.

Пример (признак равенства треугольников по двум сторонам и большему углу)

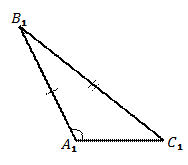
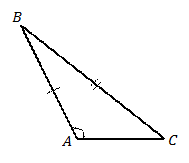
Рис. 8.

Признак равенства треугольников по двум сторонам и большему углу

Два треугольника равны, если две стороны и наибольший угол одного треугольника равны соответственно двум сторонам и наибольшему углу другого треугольника.

.

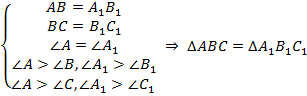Доказательство.

Если наибольшим углом окажется угол 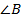, то признак доказан, т.к. он сводится к первому признаку равенства треугольником. Поэтому на Рис. 8 изображен общий случай, когда наибольшим является угол, не лежащий между указанными сторонами, например, это угол 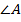. Кстати, наибольший угол 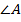не обязательно должен быть тупым, на рисунке так изображено только для наглядности.

Для доказательства равенства треугольников вспомним, что фигуры равны, если их можно совместить.

Мысленно наложим один треугольник поверх второго так, чтобы совпали точк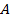и и 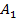. Ввиду равенства сторон 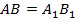и угла 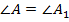несложно представить, что точк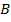и и 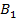тоже совпадут. Получим, что у двух сравниваемых треугольников уже совпали две вершины, но не факт, что совпадет третья ( 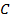и 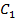), это и осталось доказать.

Докажем этот факт от противного: изобразим исходный треугольник поверх другого треугольника (в скобках указаны совпавшие вершины) и представим, что вершины 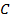и 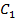не совпали, как это указано на Рис. 9.

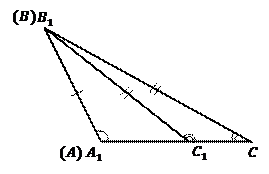
Рис. 9

Нам необходимо доказать, что ситуация несовпадения точек 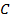и 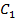невозможна.

Рассмотрим получившейся в результате наложения треугольник 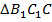. В нем стороны 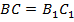по условию, следовательно, он равнобедренный, следовательно, 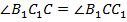. А 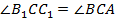, если назвать вершины, как в исходном треугольнике.

Но угол 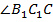является внешним для треугольника 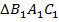, следовательно, 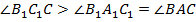. Получили такие соотношения:

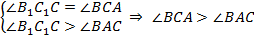, что противоречит условию задачи. Следовательно, точк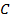и и 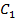совпадают, и .

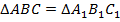Доказано.

В рамках урока мы повторили признаки равенства треугольников и две важнейшие теоремы о треугольниках.

На следующем уроке мы вспомним свойства такого частного вида треугольников, как прямоугольный треугольник.

Домашнее задание

1. На медиане 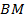треугольника 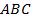отметили точку 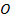так, что 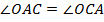. Докажите, что 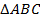– равнобедренный.

2. Равнобедренные треугольник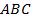и и 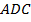имеют общее основание 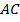. Докажите, что прямая 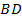– серединный перпендикуляр отрезка .

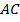3. В треугольнике 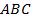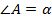, биссектрисы внешних углов при вершинах 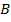и 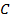пересекаются в точке 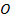. Найдите угол .

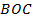4. В треугольнике 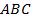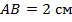, 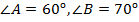. На стороне 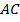отметили точку 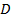так, что 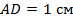. Найдите углы треугольника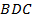

Урок 4: Повторение. Прямоугольные треугольники.

Данный урок посвящен прямоугольным треугольникам и их свойствам. Прямые углы, а значит, и прямоугольные треугольники, встречаются в жизни человека практически на каждом углу (в прямом и переносном смысле). Поэтому изучение их свойств может пригодиться не только при дальнейшем изучении курса геометрии, но и в простых жизненных ситуациях. В 7 классе были изучены самые простые свойства прямоугольных треугольников. Поскольку в 8 классе изучению более сложных свойств будет уделено достаточно большое внимание, необходимо вспомнить то, что нам уже известно про прямоугольные треугольники.