Определение треугольника. Какие треугольники называются равными? Сформулировать признаки равенства треугольников. Доказать первый признак равенства треугольников.

Билет № 1.

1. Что изучает геометрия? Разделы геометрии: планиметрия и стереометрия. Логическое строение геометрии. Что называется аксиомой, теоремой, определением? Привести примеры.

Определение треугольника. Какие треугольники называются равными? Сформулировать признаки равенства треугольников. Доказать первый признак равенства треугольников.

Задача.

Билет № 2.

Перечислить основные фигуры. Как они изображаются и обозначаются? Аксиома принадлежности точек и аксиома прямой. Сформулировать, сделать чертеж и символическую запись.

Определение серединного перпендикуляра. Доказать свойство серединного перпендикуляра.

Задача.

Билет № 3.

Взаимное расположение прямых на плоскости и в пространстве (показать на моделях и сделать чертеж; обозначение). Доказать теорему о свойстве прямых. Аксиома параллельных прямых.

Определение угла; биссектрисы угла. Доказать теорему о свойстве биссектрисы угла.

Задача.

Билет № 4.

Определение отрезка, его обозначение. Аксиома расположения точек на прямой (чертеж, символическая запись). Что называется длиной отрезка, его серединой?

Определение перпендикулярных прямых. Доказать теорему о прямой, перпендикулярной данной и проходящей через точку этой прямой.

Задача.

Билет № 5.

Какие отрезки называются равными? Аксиома измерения отрезков (формулировка, чертеж, символическая запись).

Определение равнобедренного, равностороннего треугольника. Доказать свойство углов равнобедренного, равностороннего треугольников.

Задача.

Билет № 6.

Определение полуплоскости. Аксиома разбиения плоскости и свойства разбиения (сформулировать, сделать чертеж и символическую запись).

Определение медианы. Доказать свойство медианы равнобедренного треугольника, проведенной к его основанию. Сформулировать обратные теоремы.

Задача.

Билет № 7.

Определение, изображение, обозначение луча (полупрямой). Какие полупрямые называются дополнительными? Аксиома откладывания отрезков (формулировка, чертеж, символическая запись).

Определение хорды, диаметра круга. Доказать теорему о диаметре, перпендикулярном хорде. Сформулировать обратную теорему.

Задача.

Билет № 8.

1. Определение и обозначение угла. Виды углов и их определение (сделать чертежи). Доказать свойство биссектрис вертикальных углов.

Определение вневписанной окружности. Доказать теорему о центре вневписанной окружности.

Задача.

Билет № 9.

Единицы измерения углов (градусы, минуты, секунды и перевод одних единиц в другие). Как измерять углы с помощью транспортира? Аксиома измерения углов (формулировка, чертеж, символическая запись).

Определение окружности, радиуса окружности, касательной к окружности. Доказать теорему об отрезках касательных, проведенных из одной точки к окружности.

Задача.

Билет № 10.

Определение равных углов, биссектрисы угла. Аксиома откладывания углов (формулировка, чертеж, символическая запись).

Определение окружности, описанной около треугольника. Доказать теорему о центре описанной окружности. Описать окружность около остроугольного, прямоугольного и тупоугольного треугольника.

Задача.

Билет № 11.

Определение треугольника и его элементов. Виды треугольников (по углам и по сторонам). Как называются стороны прямоугольного треугольника? Определение равных треугольников, соответственных сторон и углов.

Определение окружности, вписанной в треугольник. Доказать теорему о центре вписанной окружности. В данный треугольник вписать окружность.

Задача.

Билет № 12.

Аксиома существования треугольника, равного данному (формулировка, чертеж, символическая запись). Доказать теорему о прямой, пересекающей одну из сторон треугольника. Требования к доказательству теорем.

Алгоритм решения задач на построение. Построить треугольник по трем сторонам. Построить биссектрису угла.

Задача.

Билет № 13.

Виды треугольников по сторонам. Название сторон в равнобедренном треугольнике. Какие теоремы называются обратными? Доказать свойство биссектрисы равнобедренного треугольника, проведенной к его основанию. Сформулировать обратные теоремы.

Что значит решить задачу на построение? Построить угол, равный данному. Построить середину отрезка.

Задача.

Билет № 14.

Виды треугольников по углам. Как называются стороны в прямоугольном треугольнике? Схема доказательства от противного. Доказать теорему о пересечении прямой одной из параллельных прямых.

Какие прямые называются взаимно перпендикулярными? Что называется перпендикуляром к данной прямой? Построить прямую, перпендикулярную данной прямой и проходящую через точку, лежащую на этой прямой (не лежащую на данной прямой).

Задача.

Билет № 15.

Задача.

Билет № 16.

Задача.

Билет № 17.

Определение равнобедренного, равностороннего треугольников. Доказать свойства углов равнобедренного и равностороннего треугольников. Сформулировать и доказать признаки равнобедренного и равностороннего треугольников.

Задача.

Билет № 18.

Задача.

Билет № 19.

Задача.

Билет № 20.

Задача.

Билет № 21.

1. Определение окружности и ее элементов (центр, радиус, хорда, диаметр, дуга). Формула длины окружности; длины дуги. Определение центрального угла, его градусная мера.

2. Доказать свойство катета, лежащего против угла в 30°.

Задача.

Билет № 22.

Задача.

Билет № 23.

Задача.

Билет № 24.

Признаки параллелограмма.

Задача.

Билет № 25.

Задача.

Билет № 26.

Задача.

Билет № 27.

1. Что означают слова «фигура состоит из всех точек плоскости, обладающих определенным свойством? Определение геометрического места точек (ГМТ). Привести примеры. Алгоритм решения задач на построение методом ГМТ.

Задача.

Билет № 28.

Задача.

Билет № 29.

Задача.

Билет № 30.

Задача.

ВОПРОСЫ К УСТНОМУ ЭКЗАМЕНУ ПО ГЕОМЕТРИИ. 8 класс.

Признаки параллелограмма.

Доказательство: Возьмем любые две точки М и N выпуклого многоугольника Р. Многоугольник Р является пересечением нескольких полуплоскостей. Отрезок MN лежит в каждой из этих полуплоскостей. Поэтому он содержится и в многоугольнике Р.

Свойство 3. Сумма углов выпуклого многоугольника равна (n – 2)∙180°.

Доказательство: Возьмем внутри выпуклого многоугольника Р произвольную точку О и соединим ее со всеми вершинами многоугольника. Образуется n треугольников, сумма углов каждого из которых равна 180°. Углы при вершине О в сумме дают 360° = 2∙180°. Поэтому сумма углов многоугольника равна n∙180° - 2∙180° = (n – 2)∙180°.

Свойства параллелограмма.

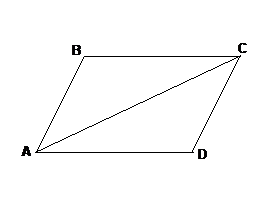Свойство 1. У параллелограмма противоположные стороны равны и противоположные углы попарно равны.

Доказательство: Проведем диагональ АС. АС – общая;

ÐВАС = ÐАСD (внутренние накрест лежащие при АВ II BC и секущей АС);

ÐВСА = ÐСАD (внутренние накрест лежащие при АD II BC и секущей АС);

Þ DАВС = DАDС (по 2 признаку).

АВ = CD; BC = AD; ÐВ = ÐD.

ÐА = ÐВАС + ÐСAD; ÐС = ÐАСB + ÐАСD; Þ ÐА = ÐС.

Свойство 2. У параллелограмма углы, прилежащие к одной стороне, в сумме дают 180°.

Доказательство:

ÐВ + ÐА =180° (внутренние односторонние при ВС II AD и секущей АB).

ÐB + ÐС =180° (внутренние односторонние при AВ II CD и секущей BC).

ÐD + ÐC =180° (внутренние односторонние при ВС II AD и секущей CD).

ÐA + ÐD =180° (внутренние односторонние при AВ II CD и секущей AD).

Свойство 3. Диагонали параллелограмма точкой пересечения делятся пополам.

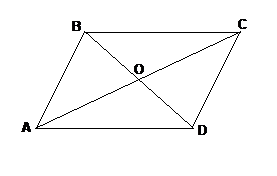Доказательство: Проведем диагонали АС и BD, пересекающиеся в точке О.

АВ = СD (по первому св-ву параллелограмма);

ÐAВO = ÐODC (внутренние накрест лежащие при АВ II CD и секущей BD);

ÐВАO = ÐOСD (внутренние накрест лежащие при АB II CD и секущей АС);

Þ DАВO = DODС (по 2 признаку).

ВO = OD; AO = OC.

Признаки параллелограмма.

Признак 1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм.

Дано: ABCD – четырехугольник; АD II BC,

АD = BC.

АВСD – параллелограмм.

Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник - параллелограмм.

Дано: ABCD – четырехугольник; АВ = СD,

АD = BC.

АВСD – параллелограмм.

Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.

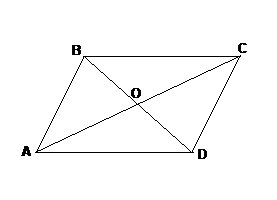Дано: ABCD – четырехугольник;

АС∩ВD = {О}; BO = OD; AO = OC.

АВСD – параллелограмм.

Рассмотрим DАВС.

АВ = ВС, АО = ОС.

Þ ВО – высота и биссектриса ÐАВC.

Þ ВС ^ AD; ÐАВO = ÐCВO.

Рассмотрим DАВD.

АВ = AD, BО = ОD.

Þ AО – высота и биссектриса ÐBАD.

Þ ÐВAO = ÐOAD.

Признаки ромба.

Признак 1. Если диагонали параллелограмма взаимно перпендикулярны, то параллелограмм является ромбом.

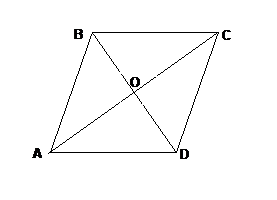Дано: ABCD – параллелограмм; АС ^ ВD.

Доказать: АВСD – ромб.

Доказательство:

АО = ОС (по свойству диагоналей параллелограмма);

ВО = ОD (по свойству диагоналей параллелограмма);

ÐАОВ = ÐВОС = ÐСОD = ÐАОD = 90°;

Þ DАОВ = DВОС = DСОD = DAOD (как прямоугольные по двум катетам);

Þ АВ = ВС = СD = AD;

Þ АВСD – ромб.

Признак 2. Если диагональ параллелограмма является биссектрисой его угла, то параллелограмм является ромбом.

Дано: ABCD – параллелограмм;

ÐВАО = ÐОАD.

Доказать: АВСD – ромб.

Доказательство:

АО – общая;

ВО = ОD (по свойству диагоналей параллелограмма);

ÐВАО = ÐDAО (по условию);

Þ DАОВ = DAOD (как прямоугольные по катету и прилежащему острому углу);

Þ АВ = AD Þ АВСD – ромб.

Рассмотрим DАВС и DВСD.

ВС – общая;

АВ = СD (по свойству параллелограмма);

АС = ВD (по условию);

ÐАВС = ÐВСD = 90° (по свойству прямоугольника).

Þ DАВС = DВCD (как прямоугольные по двум катетам).

Þ АС = ВD.

Признак прямоугольника. Параллелограмм, диагонали которого равны, является прямоугольником.

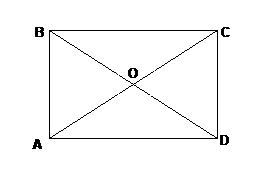Дано: ABCD – параллелограмм;

AC = BD.

Рассмотрим DАВС и DВСD.

ВС – общая;

АС = ВD (по условию);

АВ = СD (по свойству параллелограмма).

Þ DАВС = DВCD (по 3 признаку).

Þ ÐАВС = ÐВСD.

ÐАВС + ÐВСD = 180°

Þ ÐАВС = ÐВСD = 90°. ÐВ = ÐD и ÐА = ÐС (по свойству параллелограмма).

Þ ABCD – прямоугольник.

Рассмотрим DNВС и DNDE.

СN = ND (по условию); ÐВNС = ÐEND (вертикальные);

ÐBСN = ÐNDE (внутренние накрест лежащие при BC II AD и секущей CD);

Þ DNВС и DNDE (по 2 признаку) Þ BN = NE; BC = DE.

Рассмотрим DAВE. MN – средняя линия MN II AD; MN=0,5AE.

AE = AD + DE = AD + BC Þ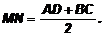

Билет № 1.

1. Что изучает геометрия? Разделы геометрии: планиметрия и стереометрия. Логическое строение геометрии. Что называется аксиомой, теоремой, определением? Привести примеры.

Определение треугольника. Какие треугольники называются равными? Сформулировать признаки равенства треугольников. Доказать первый признак равенства треугольников.

Задача.

Билет № 2.