ГЛАВА 1.Доказательство в геометрии.

СОДЕРЖАНИЕ.

ВВЕДЕНИЕ…………………………………………………………………….3-6

ГЛАВА 1.Доказательство в геометрии……………………………................7-14

1.1 Сущность доказательств в геометрии……………………………………….7

1.2 Значение доказательств геометрии………………………………………..7-8

1.3 Основные виды теорем и их структура……………………………….....8-11

1.4 Структура геометрического доказательства, его виды……………….11-14

ГЛАВА 2. Формирование умения выводить логические следствия из данных предпосылок на примере изучения темы«Треугольник» исследовательским методом……………………………………………………………………….15-68

2.1.Организация исследовательской деятельности при обучении геометрии в основной и старшей школе………………………………………………….15-21

2.2. Учебный модуль темы «Треугольник» в средней школе……………21-27

2.3Основные цели формирования у учащихся логических исследований…………………………………………………………………27-28

2.4 Организация деятельности учащихся при выработке умений выводить логические следствия.………………………………………………………28-44

2.5.Необходимые условия понимания и умения делать логические выводы………………………………………………………………………44-49

2.6.Диагностический модуль. ………………………………………………49-68

ЗАКЛЮЧЕНИЕ……………………………………………………………….69

БИБЛИОГРАФИЯ………………………………………………………….70-72

ВВЕДЕНИЕ.

Традиционно считалось, что геометрия – строго логическая наука, изучение которой в первую очередь (и главным образом) развивает логическое мышление. И.Ф.Шарынин утверждал, что геометрическое мышление, формирующееся при изучении геометрии, имеет две составляющие –наглядно-образную и логическую. Учителю необходимо создавать «мотивационный фон» особенно при объяснении нового материала в частности при доказательстве математических фактов, сколь бы очевидными они не казались, ибо по словам Д.Пойа роль доказательств в школьном математическом образовании является наиболее существенной частью вклада математики в общую культуру человека. По словам Д.Гильберта, существует поразительная гармония между наглядностью, интуицией и логическим мышлением, заключающаяся в том, что общее и абстрактное, с одной стороны и непосредственно наглядное, с другой, объединяются в единый мир идей. Поэтому доказательства математических факторов должны быть, по возможности, логически строгими и опираться при этом на имеющиеся наглядно-интуитивные представления учащегося. Знакомясь с окружающими предметами и явлениями, человек обнаруживает, что между ними существуют закономерные связи и отношения. Изучая окружающую действительность, люди узнают, например, что плавание тел зависит от их удельного веса, что сгорание приводит к возникновению тепла. Такое отражение действительности называют мышлением. Мышление есть обобщенное отражение в мозге человека предметов и явлений в их закономерных связях и отношениях. Познание в процессе мышления объективных закономерностей позволяет человеку судить на основании непосредственно наблюдаемых свойств действительности о её существенных особенностях, которые не обнаруживаются в восприятии.

Таким образом, человек не только непосредственно воспринимает внешнюю сторону предметов и явлений, но и начинает обнаруживать закономерные, существенные связи, отношения между ними, т.е. мыслит.

Например, в геометрическом понятии «треугольник» отражаются общие свойства самых различных треугольников, обладающих различной величиной, различными соотношениями сторон, различными углами и т. д.

Различают три основные формы мышления: понятие, суждение и умозаключение.

Понятие -это форма мышления, в которой отражается общее и притом существенные свойства предметов и явлений. Каждый предмет, каждое явление имеют много различных свойств, признаков. Их можно разделить на две категории- существенные и несущественные. Например, каждый отдельный треугольник имеет три угла, определенные размеры – длину сторон и площадь, определенную величину углов. Но только первый признак делает фигуру треугольником, позволяет отличить ее от других фигур: прямоугольника, круга.

Суждение – это форма мышления, содержащая утверждение или отрицание какого-либо положения относительно предметов и их свойств. В суждениях отражаются связи и отношения между предметами и их свойствами и признаками.

Умозаключение - такая форма мышления, в процессе которой человек, сопоставляя и анализируя различные предпосылки, выводит из них новое заключение. Типичный пример умозаключения – доказательство геометрических теорем. Человек пользуется в основном двумя видами умозаключений – индуктивными и дедуктивными.

Индукция– это способ рассуждения от частных суждений к общему суждению, установление общих законов и правил на основании изучения отдельных фактов и явлений.

Дедукция – это способ рассуждения от общего суждения к частному суждению, познание отдельных фактов и явлений на основании знания общих законов и правил.

В своей работе я хочу проследить как в процессе доказательства формируютсяумения выводить логические следствия из данных предпосылок на примере темы «Треугольник», каким образом это влияет на развитие логического мышления, так как развитие логического мышления является одним из важнейших элементов воспитания в школе. В геометрии наибольшее значение для развития логического мышления имеют задачи на доказательство (теоремы). Они способствуют развитию у учащихся определенности, последовательности, обоснованности мышления. На этих задачах учитель может научить учащихся таким методам познания, как анализ, синтез. Для того, чтобы ребенок начал мыслить, перед ним необходимо поставить новую задачу, в процессе решения которой он мог бы использовать приобретенные ранее знания. Мышление человека, и в частности школьника, наиболее ярко проявляется в доказательствах, выводах, при решении задач.

На уроках учитель заставляет ребенка планомерно производить анализ каких-либо предпосылок, синтезировать отдельные элементы в единое целое, сравнивать их, делать на основании известных данных обоснованные выводы и умозаключения. Ничто так, как математика, не способствует развитию мышления, особенно логического, так как предметом ее изучения являются отвлеченные понятия и закономерности.

Из всего сказанного вытекает цель:

Теоретически обосновать и продемонстрировать эффективность применения исследовательского метода для формирования умения у учащихся выводить логические следствия из данных предпосылок при изучении темы «треугольник».

Для реализации цели работы нами было организовано исследование, объектом которого является процесс формирования правильного мышления учащихся, а предметом - процесс формирования у учащихся умения выводить логические следствия из данных предпосылок при изучении темы «Треугольник».

В процессе исследования нами обосновывалось следующая гипотеза: формирование у учащихся умения выводить логические следствия из данных предпосылок наиболее эффективно проводить при изучении темы «Треугольник» исследовательским методом.

Задачи:

- определить роль логического мышления в процессе обучения школьников;

- изучить литературу, раскрывающую основные виды теорем, их структуру;

-раскрыть сущность формирования умений вывода следствий из имеющихся предпосылок;

- проследить и раскрыть структуру геометрического доказательства;

-рассмотреть методы формирования умений учащихся проводить логические исследования при доказательстве теорем и следствий из имеющихся предпосылок;

Пример 1.

Известная теорема о том, что сумма внутренних углов треугольника равна 180, доказывается на основании свойств параллельных прямых. Что указывает на непосредственную связь между теорией параллельных прямых и свойствами сумм внутренних углов многоугольников.

Точно так же на свойства параллельных прямых опирается вся теория подобия фигур.

Итак, подводя итоги всему изложенному о необходимости доказательства, мы можем сказать следующее:

а) в геометрии только небольшое число основных истин – аксиом – принимается без доказательства. Остальные же истины – теоремы – доказываются на основании этих аксиом путем построения ряда умозаключений.

б) в правильно построенном доказательстве опираться только на известные предпосылки или аксиомы.

в) доказательство необходимо также для обоснования сущности доказываемого предложения , т.е. применимости его ко всем частным случаям.

г) наконец, при помощи доказательств геометрические истины приводятся в стройную систему научных знаний, в которой раскрываются все внутренние связи между различными свойствами пространственных форм

Пример 2.

Пусть дана теорема: «В равнобедренном треугольнике углы при основании равны».

Обратная данной: «Если углы при основании треугольника равны ,то этот треугольник равнобедренный».

Противоположная теорема данной «Если треугольник не равнобедренный, то углы при основании не равны».

Обратная противоположной «Если в треугольнике углы при основании не равны, то этот треугольник не равнобедренный ».

В теореме различают условие и заключение. Во многих современных учебниках написано: «Условие теоремы – это то, что дано, а заключение – то, что требуется доказать». Также про заключение написано, что оно выражает факт, который в силу условия неизбежно имеет место. Ученый Адамар возвращался к этой мысли. Он считал необходимым подчеркнуть ее: «Чтобы провести это рассуждение надо, основываясь на условие теоремы и предполагая, что это условие выполнено, вывести из него факты, указанны в заключении».

В теореме о равенстве треугольников утверждается, что если треугольники имеют по три равные стороны, то они обязательно равны. Авторы учебников понимают, что условие теоремы является необходимой предпосылкой заключения. Но ученикам это остается неизвестным, многим в начале изучения геометрии, а некоторым и в дальнейшем.

Пример 3.[18]

Теорему «Равные треугольники» можно записать в другой форме «Если три стороны одного треугольника равны трем сторонам другого треугольника , то эти треугольники равны». Для чего теорему записывают таким образом? Чтобы сразу было видно, что дано (на что нужно опираться при доказательстве), и что надо доказать.

Яснее становится постановка задачи и, следовательно, легче найти доказательство.

Но, следует помнить, что утверждения бывают истинные и ложные. Что нужно сделать, чтобы опровергнуть неверное суждение? Чтобы опровергнуть неверное утверждение, достаточно привести один противоречащий пример (контрпример) – пример, удовлетворяющий условию этого утверждения, но не удовлетворяющий его заключению. Рассмотрение контрпримеров помогает ученику понять необходимость каждого условия теоремы, облегчает запоминание. Построение контрпримеров позволяет отсекать неверные гипотезы при решении задач, помогает, когда уточняется формулировка теоремы и при поиске ее доказательства. Чтобы класс освоил построение контрпримеров, нужно на одном из уроков рассмотреть несколько контрпримеров и дать подобные задачи на дом. Затем, время от времени, после доказательства теоремы, опустив какое-то условие, предложить классу доказать, что полученное утверждение неверно.

Пример 4. [18]

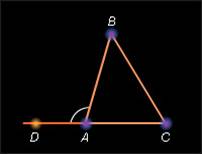
Если две стороны и угол одно треугольника равны двум сторонам и углу другого треугольника такие треугольники равны. (верно ли это утверждение?) Ответ: Нет.

Контрпример: Рассмотрим равнобедренный треугольник АВС с основанием АС и отметим точку Д на продолжении стороны АС . Тогда треугольники ДВС и ДВА обладают указанным свойством, но не являются равными.

Услышав сообщение учителя «Сегодня мы докажем теорему», ученик сразу спрашивает: «А зачем?» Очень трудно осваивать теорему, если считаешь, что она не нужна. Учитель не должен забывать об этом. Не только о первой, но о каждой теореме нужно сказать несколько слов о том, как возникла эта проблема, зачем нужно ее решать. Учителю – то известно ее значение, связь с другим материалом.

1.4. Структура геометрического доказательства, его виды.

Рассмотрим структуру геометрического доказательства. Логическое доказательство состоит из трех частей:

1. Тезис – доказываемое положение

2. Основания или аргументы – суждения, на которые опирается доказательство.

3. Демонстрация или способ доказательства – рассуждение, выводящее из истинности принятых оснований истинность доказываемого тезиса.

Короче их можно охарактеризовать так:

1. Тезис– что доказывается

2. Аргументы – чем доказывается

3. Демонстрация– как доказывается

Абсолютно необходимыми условиями возможности перехода к демонстрации являются:

1. Ясное и четкое понимание самого тезиса и всех предшествующих ему предложений, необходимых для доказательства.

2. Установление точного смысла тезисов, встречающихся в тезисе и аргументах.

Без предварительного выполнения этих условий переход к демонстрации

невозможен.

Сам термин «доказательство» употребляется в математике в смысле «рассуждение», устанавливающее истинность того или иного суждения, связь мыслей, приводящая к определенному выводу относительно тезиса. Иначе говоря, доказательство есть демонстрация – выведение тезиса из аргумента.

Обычно в процессе доказательства в качестве аргументов используются:

а) данные, содержащиеся в условии теоремы;

б) ранее доказанные теоремы;

в) аксиомы;

г) определения.

Аргументы используются в посылках и притом так, чтобы из каждой пары посылок необходимо следовал вывод. Выводное суждение каждого умозаключения (силлогизма) является уже аргументом по отношению к последующим силлогизмам. Выводное суждение последнего силлогизма должно содержать доказываемый тезис.

Следовательно, доказательство представляет собой систему умозаключений, логическую цепь силлогизмов, которая начинается с данных или ранее известных положений и заканчивается доказываемым тезисом. Простейшие доказательства могут состоять из одного силлогизма. В этом случае выводное суждение, являющееся доказываемым тезисом, предшествует посылкам и доказательство сводится к подбору посылок из которых следовал бы тезис.

Пример5.

Доказать, что сумма углов треугольника равна 180 градусов

Подбираем посылки:

1) развернутый угол составляет 180 градусов .

2) углы треугольника в сумме составляют развернутый угол.

Они и служат оправданием тезиса.

Выделяют следующие виды доказательств:

1. Прямое доказательство.

Прямым доказательством называется доказательство, в котором аргументы непосредственно доказывают тезис. Прямые доказательства могут быть синтетическими и аналитическими.

2. Косвенное доказательство.

Косвенным доказательством называется доказательство, в котором истинность тезиса обосновывается посредством опровержения истинности других положений.

Пусть требуется доказать, что «А» есть «В» (тезис).В случае прямого доказательства мы ищем основания , из которых вытекает данный тезис; в косвенном апагогичном доказательстве доказываем ложность суждения, противоречащего тезису, т.е. ложность суждения «А» не есть «В» (антитезис). Косвенное апагогическое доказательство называют «доказательством от косвенного» или от противного.

Пример 6.

При доказательстве теоремы «Против большего угла в треугольнике лежит большая сторона»

Большая посылка : угол С > угла В

а) либо АВ= АС;

в) либо АВ < АС ;

г) либо АВ > АС.

Приводим к нелепости две первые возможности:

Силлогизмы примут вид:

1. Если : угол С > угла В то возможны три случая:

или АВ= АС; либо АВ < АС ; либо АВ > АС

Опираясь на ранее изученную теорию, получаем:

2. суждение АВ= АС – ложно

суждение АВ < АС – ложно

Следовательно, суждение АВ > АС – истинно.

Посылками в решении этой задачи служат предложения:

1)У равностороннего треугольника стороны равны.

2)У равнобедренного треугольника две стороны равны.

Это и доказывает наше утверждение.

Силлогизмом – называется дедуктивное умозаключение, в котором из двух данных суждений (посылок) выводится третье суждение (заключение).

Пример 7.

Является ли равносторонний треугольник равнобедренным?

Решение: Треугольник АВС – равносторонний и поэтому ____=____=___.

Поскольку ,например, ____= _____, его можно считать равнобедренным с основанием ____. Если рассмотреть другие пары сторон, то его можно считать равнобедренным с основанием _______.

Посылками в решении этой задачи служат предложения:

1)У равностороннего треугольника стороны равны.

2)У равнобедренного треугольника две стороны равны.

Это и доказывает наше утверждение.

Правила:

1. Термин, не распределенный в посылках, не может быть распределен в заключении.

2. Из двух отрицательных посылок нельзя вывести никакого заключения.

3. Если одна из посылок есть отрицательное суждение, то и заключение может быть только отрицательным.

4. Из двух частных посылок не следует никакого заключения.

5. Если одна из посылок частная, то и заключение может быть только частным.

Следует отметить, что доказательство может проходить в нестандартной форме, например, путем возбуждения сомнений в справедливости теоремы. Только зная эти основные моменты, мы можем более детально понять сущность самого процесса доказательства.

Пример 8

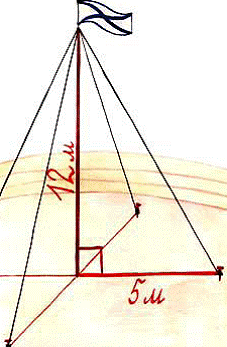
В качестве иллюстрации учебного исследования можно привести фрагмент урока геометрии по теме «Теорема Пифагора».Мотивирующей (исходной) задачей может служить следующая задача: «Для крепления мачты нужно установить 4 троса. Один конецкаждого троса должен крепитьсяна высоте 12 м, другой на земле нарасстоянии 5 м от мачты. Хватитли 50 м троса для крепления мачты?»

Анализируя математическую модель этой практической задачи, учащиеся формулируют проблему – нужно найти гипотенузу прямоугольного треугольника по двум известным катетам.

Для решения этой проблемы можно организовать практическую работу исследовательского характера, предложив учащимся задание по рядам: построить прямоугольные треугольники с катетами 12 и 5; 6 и 8; 8 и 15 см и измерить гипотенузу. Результаты заносятся в таблицу.

а12 6 8

b5 8 15

с13 10 17

Затем учащимся предлагается выразить формулой зависимость между длинами катетов и гипотенузой в прямоугольных треугольниках. Школьники выдвигают свои гипотезы, которые обсуждаются.

После установления зависимости между сторонами прямоугольного треугольника эмпирический вывод требует теоретического обоснования, т.е. доказывается теорема Пифагора.

В качестве домашнего задания по этой теме можно предложить

исследовательскую работу со следующей мотивирующей задачей:

«Кто же на самом деле открыл теорему Пифагор? Почему она долгое время называлась «теоремой невесты»? Существуют ли другие доказательства теоремы?»

Цель этой исследовательской работы – научить учеников использовать дополнительную литературу, применять Интернет в собственной

образовательной деятельности.

Несколько примеров мотивирующих задач.

Пример 9 [24]

При изучении темы «Сумма внутренних углов треугольника»в качестве исходного задания можно предложить такую задачу: «Построить треугольник по трем заданным углам:

1) . А = 90о, . В = 60о, . С = 45о;

2) . А = 70о, . В = 30о, . С = 50о;

3) . А = 50о, . В = 60о, . С = 70о».

Учащиеся, вооружившись линейкой и транспортиром, начинают строить треугольники. В первом случае, построив углы А и В и отложив угол в 45о от луча АС (или ВС, кому как нравится), ребята увидят, что вместо треугольника получается четырехугольник. Во втором случае независимо от того, какие первые два угла школьники выбирают для построения, всегда получается треугольник, третий угол которого больше, либо меньше заданного. И только в третьем случае выстраивается треугольник по трем заданным углам.

По окончании уже можно выдвинуть предположение о сумме углов треугольника. Здесь уместен провокационный вопрос:«В каком треугольнике, по вашему мнению, сумма внутренних углов больше, в остроугольном или тупоугольном?» Практика показывает, что почти в каждом классе найдутся несколько человек, которые, зная, что тупой угол всегда больше острого, по аналогии скажут, что сумма внутренних углов тупоугольного треугольника больше, чем остроугольного. Далее им предлагается на практике проверить свое утверждение.

Математика дает широкое поле для исследования. Изучая математику, учащиеся кратко повторяют путь человечества, который оно прошло, добывая математические знания.

Пример 10 [24]

Рассматриваем многогранники. Учащиеся могут самостоятельно прийти к соотношению между числом вершин, граней и ребер для любого выпуклого многогранника, которое выражается известной формулой Эйлера.

Для эксперимента учащимся предлагаются модели различных выпуклых многогранников, используя которые, они заполняют таблицу.

Тетраэдр

Октаэдр

Икосаэдр

Додекаэдр

Угольная пирамида

8-угольнаяпризма

…

Не следует предлагать учащимся вычислять значения готового выражения

В+ Г– Р.

Больше пользы будет в том случае, если они сами, выполняя действия над числовыми характеристиками, получат требуемое равенство. Лишь в случае значительных затруднений можно оказать им некоторую помощь.

Иногда за урок удается решить одну крупную проблему, или же

урок может содержать несколько мелких проблемных заданий.

Кроме уроков-исследований существуют также мини-исследования.В них присутствуют лишь некоторые исследовательские элементы. Выполнение задания занимает несколько минут.

Вот примеры совсем небольших проблем-вопросов: «Почему треугольник назван «треугольником»? Можно ли дать ему другое название, также связанное с его свойствами?»

Кроме исследовательской работы на уроках возможна самостоятельная исследовательская работа учащихся. Виды самостоятельных исследовательских работ разнообразны.

Самостоятельная исследовательская работа учащихся предполагает наличие основных этапов, характерных для научного исследования.

Основные этапы научного исследования

1 Постановка проблемы

2 Знакомство с литературой по проблеме исследования

3 Сбор собственного материала

4 Анализ, обобщение

5 Выводы

Результат исследования неизвестен заранее.

Конечный результат обладает практической ценностью.

Учащиеся 5–7-х классовприобретают простейшие знания, умения и навыки, необходимые для выполнения исследовательской работы. Детей обучают основам самостоятельной деятельности, развивают нестандартное мышление.

Учащиеся 8 – 9-х классоввыполняют исследовательские задания творческого характера. На этом этапе усложняются формы исследовательской работы, увеличивается их объем. Учащимся можно предложить следующие темы для рефератов и исследовательских работ:

Замечательные точки в треугольнике.

Различные способы доказательства теоремы Пифагора.

В 10 – 11 классахпроисходит углубление знаний по методике исследования и обработке результатов. Все это осуществляется в процессе длительной самостоятельной работы

Упражнения.

Этому курсу присущ систематизирующий и обобщающий характер изложений, направленность на закрепление и развитие умений и навыков, полученных в основной школе. Высокий уровень абстрактности изучаемого материала, логическая строгость систематического изложения соединяется с привлечением наглядности на всех этапах учебного процесса и постоянным обращением к опыту учащихся. Умение изображать важнейшие геометрические тела, вычислять их объёмы и площади поверхностей имеют большую практическую значимость. Для эффективной реализации курса необходимо использовать разнообразные формы, методы и приёмы обучения, делая особый упор на развитие самостоятельности, познавательного интереса и творческой активности учащихся. Для этой цели проводят уроки:

1. лекции;

2. уроки консультации;

3. самостоятельные работы;

4. зачеты;

5. итоговые контрольные работы.

Для тех учащихся, которые хотят продолжить образование, связанное с геометрией, практикум решения задач исследовательским методом будет способствовать успешной сдаче единого государственного экзамена по математике, вступительного экзамена в ВУЗ и успешного обучения в ВУЗ-е

Решение стереометрических задач на свойства геометрических тел, нахождение площадей поверхностей и объемов этих тел, позволяют получить углубленные знания по геометрии и дают ориентацию на инженерные профессии, связанные с математикой.

Пример:

Задача 1. В правильной четырехугольной пирамиде боковое ребро наклонено к плоскости основания под углом 45°. Найдите плоский угол при вершине.

Исследование при решении этой задачи можно провести без чертежа:

Первый способ:

Пусть боковое ребро равно a. Оно наклонено к основанию под углом 45°, поэтому проекция этого ребра равна половине диагонали основания, то есть 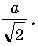Вторая половина диагонали образует с ней прямой угол и дает прямоугольный равнобедренный треугольник, гипотенуза которого равна a, следовательно, боковая грань – равносторонний треугольник с углом при вершине 60°

Второй способ:

Теорема. Если некоторая прямая образует с прямой на плоскости угол , с проекцией на эту плоскость ,
а проекция с прямой на плоскости угол , то

cos  = cos  cos .

Применительно к данной задаче это выглядит так.

Обозначим через  угол между боковым ребром и ребром основания, между боковым ребром и проекцией – через  ( = 45°), между проекцией и ребром основания – через  ( = 45°). Тогда по теореме трех косинусов имеем 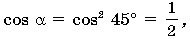следовательно,  = 60°.

Так как боковая грань – равнобедренный треугольник, то в данном случае он и равносторонний. Плоский угол при вершине равен 60°.

Иначе задачу можно сформулировать так: плоский угол при вершине равен 60°. Найдите угол наклона бокового ребра к основанию.

Задача2.

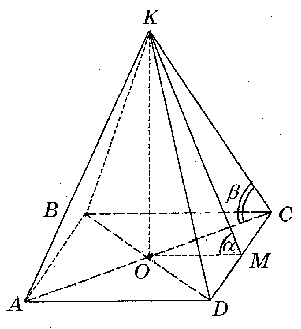В правильной четырехугольной пирамиде площадь боковой поверхности в n раз больше площади основания. Определите угол наклона бокового ребра к основанию.

Решение. Обозначим угол KCO через – , линейный угол двугранного угла CD – угол KMO – через .

Учащиеся знают, что если некая фигура образует с плоскостью угол , а проекция этой фигуры на плоскость имеет площадь S_о, то площадь фигуры 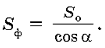Следствием из этой теоремы является зависимость между площадями основания правильной пирамиды и боковой поверхности. В рассматриваемом случае имеем

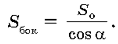
Так как площадь боковой поверхности в n раз больше площади основания, то имеем 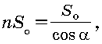откуда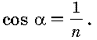

Решение задачи сводится к определению угла , если известен угол .

Углы  и  принадлежат двум прямоугольным треугольникам, «связанным» общим катетом KO. Вторые катеты OC и OM легко вычисляются один через другой (гипотенуза и катет прямоугольного равнобедренного треугольника). Поэтому используем функцию тангенс. Имеем

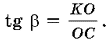
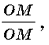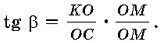Используем следующую «изюминку»: умножим эту дробь на дробь имеем Перепишем иначе это выражение: 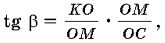имеем 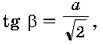где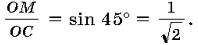

Задача свелась к определению tg , если известен его косинус. Как же это сделать?

Учащиеся знают формулу

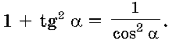
Но ученик может «случайно» забыть формулу или ошибиться в 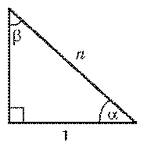преобразованиях. Я же в свое время заставлял учеников ни в коем случае не решать по формулам, а находить значение любой тригонометрической функции через известную формулу только устно.

Представим в уме прямоугольный треугольник. Обозначим один из острых углов через a, гипотенузу – через n, прилежащий к углу a катет положим равным 1. Второй катет по теореме Пифагора равен 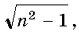тогда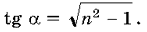

Задача решена. Имеем

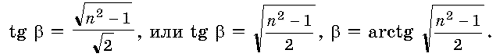
Без использования этих двух «изюминок» решение задачи было бы сложнее. Для самоконтроля можно решить следующую задачу.

В правильной шести- или n-угольной пирамиде высота образует с боковым ребром угол a. Определите, какой угол образует высота с боковой гранью.

Ход урока

(мотивация)На предыдущих уроках мы с вами изучали признаки и свойства параллельности прямых. И сегодня на уроке, полученные по этой теме знания, помогут сделать открытие. Фигура, с которой мы будем работать, вам уже знакома. А сегодня мы найдем сумму всех ее углов.

(сбор фактического материала)

1) Сформулируйте определение треугольника.

(Треугольник – это фигура, образованная тремя точками, не лежащими на одной прямой, и отрезками, попарно соединяющими эти точки.)

2) Назовите элементы треугольника. (Вершины, стороны, углы.)

3) Какие треугольники различают? (По сторонам: разносторонние, равносторонние, равнобедренные; карточки – треугольники)

4) Треугольники различают и по углам. Давайте с вами составим рассказ по теме « Угол».

Для помощи используем план, записанный на доске.

1. 1. Угол – это фигура, …

2. Если …, то угол называют …

3. Внутренний угол треугольника – это …

Ответы:

1. Угол – это фигура, образованная двумя лучами, выходящими из одной точки. Лучи называют сторонами угла, а точку – вершиной.

2. Если величина угла 90⁰, то угол называют прямым.

Если – 180⁰, то развернутым. Если больше 0⁰. но меньше 90⁰, то называют острым. Если больше 90⁰, но меньше 180⁰, называют тупым. Т.о. углы бывают тупые, острые, прямые и развернутые.

3. Внутренний угол треугольника – угол, образованный его сторонами, вершина треугольника является вершиной его угла.

Значит, в треугольнике углы могут быть различными: тупыми, острыми и прямыми.

5)Начертите угол: (1 ученик делает на доске)

1 – ряд – тупой; 2 – ряд – прямой; 3 – ряд острый.

Дополните рисунок до треугольника. Что для этого нужно сделать?

(Взять по точке на сторонах угла и соединить их отрезками.)

6) Полученные треугольники можно назвать: тупоугольными, прямоугольными и остроугольными. (карточки – треугольники)

Обратите внимание, что у остроугольного треугольника все углы острые.

7)Бывают ли треугольники с двумя прямыми углами? С двумя тупыми углами? С прямым и тупым углом? Как это обосновать? Сделать рисунок. К доске выходит ученик и выполняет следующие рисунки:

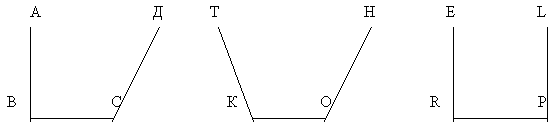
Далее идет коллективное обсуждение.

(исследование)

Лучи ВА и СО, КТ и ОН. КЕ и PL пересекаются, значит, треугольник не получится. Сумма односторонних углов в I случае больше, чем 180⁰ , во II случае также больше, чем 180⁰ , а в III случае — равна 180°. В III случае прямые параллельны, а в первых двух случаях прямые расходятся. Делают вывод, что треугольник не может иметь два тупых или два прямых угла. А также в треугольнике не может быть одновременно один тупой и один прямой углы.

(постановка проблемы)

8) Мы выполнили некоторую практическую работу, сделали обоснование того факта, что треугольник не всегда существует. Его существование зависит от величин углов. Как можно узнать, чему равна сумма углов треугольника? Практически — измерение, теоретически — рассуждением

9) На дом вам было дано задание: построить треугольники, измерить их углы и найти сумму углов каждого треугольника. Чему равна сумма углов каждого треугольника? (180°, 179°, 182°, 185°, 178°...)

Что заметили? Все суммы близки к 180°. Значит, сумма углов треугольника равна 180⁰.

(выдвижение гипотезы)

10) Итак, ребята, у вас появилась гипотеза, сумма углов треугольника равна 180 . Однако, у многих из вас получились результаты, близкие к 180°, но не 180°, Почему? Измеряя, мы получаем приближенные значения. Сумма углов треугольника была практическим путем установлена, вероятно, еще в Древнем Египте, Прокл утверждал, что доказательство этого факта было известно еще в V в. до н. э. Однако у нас с вами есть гипотеза: сумма углов треугольника равна 180 , которую можно проверить еще одной практической работой: где еще сегодня называли это число? Величина развернутого угла.

(систематизация и анализ полученного материала)

На столах лежат треугольники. Путем перегибания соберем углы треугольника в одну точку.

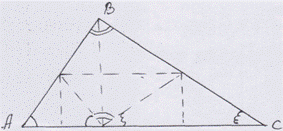
Что у нас получилось? Что сумма углов треугольника равна 180⁰.

11) Более точно это можно доказать, используя теорему о сумме внутренних углов треугольника - одну из самых важных теорем геометрии. Записать название темы.

( проверка гипотезы)

Сформулируйте теорему: Сумма углов треугольника равна 180⁰

Попробуем доказать теорему, “собрав” все углы треугольника в одну вершину (на доске выполняется чертеж).

А

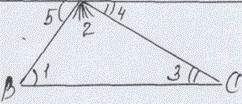
“ Собрать углы” - значит, “ взять углы”, равные данным.

Когда < 4=<3 (< 5=<1)? (При параллельности прямой а и стороны ВС)

Известно:

<5 + <2 + <4 =180°. (развернутый угол)

<1 + <2+ <3 = 180°.

(доказательство или опровержение гипотез)

12) Доказать теорему , делая кратную запись:

ДАНО: АВС,<1, <2, <3 - внутренние.

ДОКАЗАТЬ: <1 + <2 + <3 = 180°.

Доказательство:

1) Проведем прямую а // ВС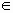, А а.

2) <5 = <1 (внутренние накрест лежащие при а // ВС и секущей АВ)

<4 = <3 ((внутренние накрест лежащие при а // ВС и секущей АС)

3) <5 + <2 + <4 = 180°. (развернутый угол)

4) <1 + <2 + <3 = 180°. Ч. Т. Д.

13) Повторить план доказательства:

- провести прямую через одну из вершин параллельно противолежащей стороне;
- составить пары равных углов;
- представить развернутый угол в виде суммы углов;
- заменить слагаемые равными им углами треугольника.

14) Записать теорему и доказательство