Коэффициенты местных гидравлических сопротивлений систем теплоснабжения и отопления.

Все гидравлические потер и энергии делятся на два типа: потери на трение по длине трубопроводов и местные потери, вызванные такими элементами трубопроводов, в которых вследствие изменения размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и возникновение вихреобразования.

Трубопроводы, по которым течет жидкость, часто имеют в своем составе всевозможные сужения, расширения, повороты и дросселирующие устройства, называемые простейшими местными гидравлическими сопротивлениями. В практических расчетах трубопроводов обычно руководствуются следующим правилом. Если длина трубопроводов значительна, а местных сопротивлений немного, то потери напора в местных сопротивлениях не учитывают, но для компенсации этих потерь длину трубопровода при расчете увеличивают на 5 - 10%.
Если трубопроводы короткие, а местных сопротивлений много, то потери напора в них учитывают самым тщательным образом.

Рассмотрим простейшие местные сопротивления при турбулентном режиме течения в трубе.

1. Внезапное расширение русла.

Потеря напора (энергии) при внезапном расширении русла расходуется на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание вращательного непрерывного движения жидких масс с постоянным их обновлением.

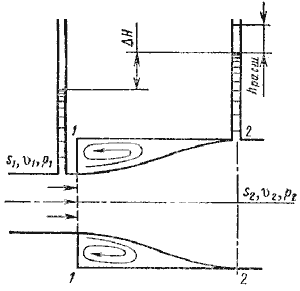
Рисунок 24 – Внезапное расширение трубы

При внезапном расширении русла (трубы) (рисунок 19) поток срывается с угла и расширяется не внезапно, как русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии. Рассмотрим два сечения потока: 1-1 - в плоскости расширения трубы и 2-2 - в том месте, где поток, расширившись, заполнил все сечение широкой трубы. Так как поток между рассматриваемыми сечениями расширяется, то скорость его уменьшается, а давление возрастает. Поэтому второй пьезометр показывает высоту на ΔH большую, чем первый; но если бы потерь напора в данном месте не было, то второй пьезометр показал бы высоту большую еще на h_расш. Эта высота и есть местная потеря напора на расширение, которая определяется по формуле:

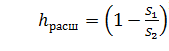(22)

где S1, S2 - площадь поперечных сечений 1-1 и 2-2.

Это выражение является следствием теоремыБорда, которая гласит, что потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей

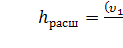(23)

Выражение (1 – S₁/S₂ )² обозначается греческой буквой ζ (дзета) и называется коэффициентом потерь, таким образом

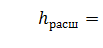(24)

2. Постепенное расширение русла.

Расширяющаяся труба называется диффузором. Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.

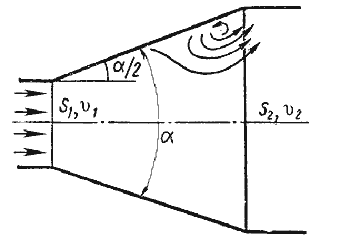
Рисунок 25 – Постепенное расширение трубы

Кроме того, в диффузоре имеются и обычные потери на терние, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:

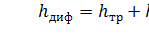(25)

где h_тр и h_расш - потери напора на трение и расширение (вихреобразование).

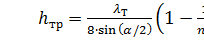(26)

где n = S₂/S₁ = ( r₂/r₁ ) ² - степень расширения диффузора. Потеря напора на расширение h_расш имеет ту же самую природу, что и при внезапном расширении русла

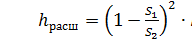(27)

где k - коэффициент смягчения, при α= 5…20°, k = sinα.

Учитывая это полную потерю напора можно переписать в виде:

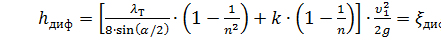(28)

откуда коэффициент сопротивления диффузора можно выразить формулой

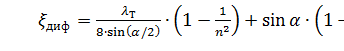(29)

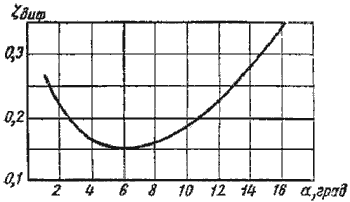
Рисунок 26 – Зависимость ζ_диф от угла

Функция ζ = f(α) имеет минимум при некотором наивыгоднейшем оптимальном значении угла α, оптимальное значение которого определится следующим выражением:

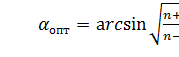(30)

При подстановке в эту формулу λ_Т =0,015…0,025 и n = 2…4 получим α_опт = 6 (рисунок 26).

3. Внезапное сужение русла.

В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока.

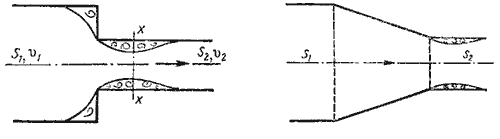
Рисунок 27 – Внезапное сужение трубы

Рисунок 28 – Конфузор

Полная потеря напора определится по формуле:

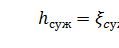(31)

где коэффициент сопротивления сужения определяется по полуэмпирической формуле И.Е. Идельчика:

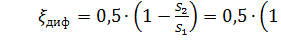(32)

в которой n = S₁/S₂ - степень сужения.

При выходе трубы из резервуара больших размеров, когда можно считать, что S₂/S₁ = 0, а также при отсутствии закругления входного угла, коэффициент сопротивления ζ_суж = 0,5.

4. Постепенное сужение русла.

Данное местное сопротивление представляет собой коническую сходящуюся трубу, которая называется конфузором (рисунок 27). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение

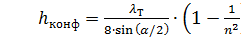(33)

где коэффициент сопротивления конфузора определяется по формуле

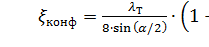(34)

в которой n = S₁/S₂ - степень сужения.

Небольшое вихреобразование и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической. Закруглением входного угла можно значительно уменьшить потерю напора при входе в трубу. Конфузор с плавно сопряженными цилиндрическими и коническими частями называется соплом (рисунок 29).

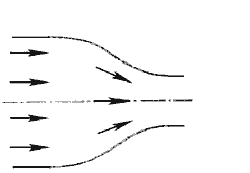
Рисунок 29 – Сопло

5. Внезапный поворот трубы (колено).

Данный вид местного сопротивления (рисунок 30) вызывает значительные потери энергии, т.к. в нем происходят отрыв потока и вихреобразования, причем потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле

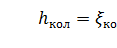(35)

где ζ_кол - коэффициент сопротивления колена круглого сечения, который определяется по графику в зависимости от угла колена δ (рисунок 31).

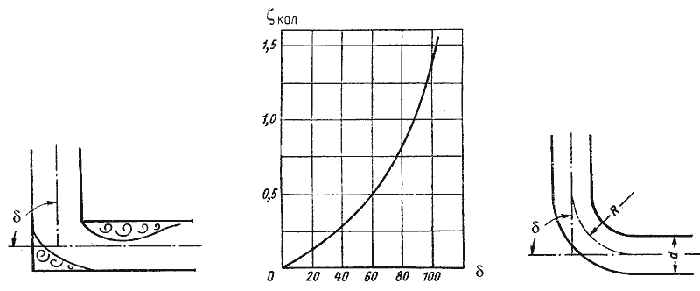
Рисунок 30 - Внезапный поворот трубы (колено).

Рисунок 31 - Зависимости ζкол от угла δ

Рисунок 32 – Отвод

6. Постепенный поворот трубы (закругленное колено или отвод). Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R/d рисунок 32). Коэффициент сопротивления отвода ζ_отв зависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.

Для отводов круглого сечения с углом δ= 90 и R/d 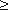1 при турбулентном течении можно воспользоваться эмпирической формулой:

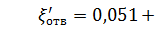(36)

Для углов δ 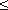70° коэффициент сопротивления

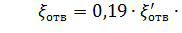(37)

а при δ 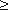100°

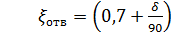(38)

Потеря напора в колене определится как

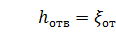(39)

Иногда при расчете систем трубопроводов с большим числом местных сопротивлений потери напора в них вычисляют по их эквивалентным длинам. Длиной, эквивалентной данному местному сопротивлению, считается такая длина прямой трубы (того же диаметра, как и номинальный диаметр рассчитываемого трубопровода), на протяжении которой гидравлические потери равны потерям в данном сопротивлении. В результате такой замены все местные сопротивления в системе устраняются, длины труб соответственно увеличиваются и далее рассчитывается только прямолинейный трубопровод.

Пусть, например, надо заменить местное сопротивление С коэффициентом ζ трубой эквивалентной длины lэ диаметром d.
Значение эквивалентных длин для каждого значения ζ берется из таблиц соответствующих справочников. Таблицы КМС приведены в приложениях.

Для расчета характеристики участка составляем таблицу коэффициентов местного сопротивления циркуляционного кольца (таблица 22)

Таблица 22 – Ведомость коэффициентов местных сопротивлений циркуляционного кольца

Номер участка	коэффициент местного сопротивления	Диаметр, мм	Значение ξ	∑ξ
0-1
1-2
…