Элементы трехпроекционного комплексного чертежа точки

Для определения положения геометрического тела в пространстве и получения дополнительных сведений на их изображениях может возникнуть необходимость в построении третьей проекции. Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П₁и фронтальной плоскости проекций П₂ (рисунок 62, а). В результате пересечения фронтальной П₂и профильной П₃плоскостей проекций получаем новую ось П₂/П₃, которая располагается на комплексном чертеже параллельно вертикальной линии связи A₁A₂ (рисунок 62, б). Третья проекция точки А — профильная — оказывается связанной с фронтальной проекцией А₂новой линией связи, которую называют горизонтальной. Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A₁A₂ _|_ А₂А₁и А₂А₃, _|_ П₂/П₃.

Положение точки в пространстве в этом случае характеризуется ее широтой— расстоянием от нее до профильной плоскости проекций П₃, которое обозначим буквой р.

Полученный комплексный чертеж точки называется трехпроекционным.

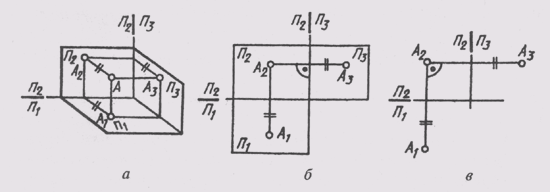
Рисунок 62 – Трехпроекционный чертеж точки А

В трехпроекционном чертеже глубина точки АА₂проецируется без искажений на плоскости П₁и П₂ (рисунок 62, а). Это обстоятельство позволяет построить третью — фронтальную проекцию точки А по ее горизонтальной А₁и фронтальной А₂проекциям (рисунок 62, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A₂A₃ _|_A₂A₁. Затем в любом месте на чертеже провести ось проекций П₂/П₃ _|_ А₂А₃, измерить глубину f точки на горизонтальномполе проекции и отложить ее по горизонтальной линии связи от оси проекций П₂/П₃. Получим профильную проекцию А₃точки А.

Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции.

Необходимо отметить, что на комплексных чертежах, как правило, не ограничивают плоскости проекций и положение их задают осями (рисунок 62, в). В тех случаях, когда условиями задачи этого не требуется, проекции точек могут быть даны без изображения осей (рисунок 63, а, б). Такая система называется безосновой. Линии связи могут также проводиться с разрывом (рисунок 63, б).

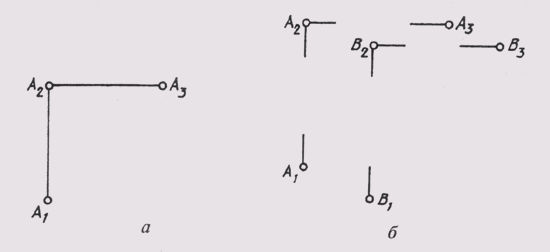
Рисунок 63 – Задание плоскостей проекций

Положение точки в пространстве трехмерного угла

Расположение проекций точек на комплексном чертеже зависит от положения точки в пространстве трехмерного угла. Рассмотрим некоторые случаи:

· точка расположена в пространстве (рисунок 62). В этом случае она имеет глубину, высоту и широту;

· точка расположена на плоскости проекций П₁— она не имеет высоты, П₂ — не имеет глубины, Пз — не имеет широты;

· точка расположена на оси проекций, П₂/П₁ не имеет глубины и высоты, П₂/П₃— не имеет глубины и широты и П₁/П₃не имеет высоты и широты.

Конкурирующие точки

Две точки в пространстве могут быть расположены по-разному. В отдельном случае они могут быть расположены так, что проекции их на какой-нибудь плоскости проекций совпадают. Такие точки называются конкурирующими.На рисунке 64, а приведен комплексный чертеж точек А и В. Они расположены так, что проекции их совпадают на плоскости П₁ [А₁ == В₁]. Такие точки называются горизонтально конкурирующими.Если проекции точек A и В совпадают на плоскости П₂ (рисунок 64, б), они называются фронтально конкурирующими.И если проекции точек А и В совпадают на плоскости П₃ [А₃ == B₃] (рисунок 64, в), они называются профильно конкурирующими.

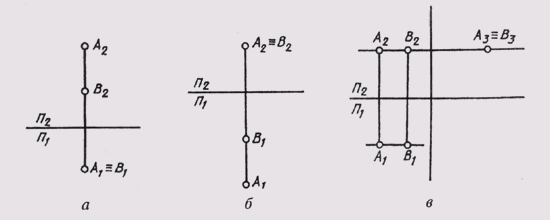
Рисунок 64 – Проекции конкурирующих точек

По конкурирующим точкам определяют видимость на чертеже. У горизонтально конкурирующих точек будет видима та, у которой больше высота, у фронтально конкурирующих — та, у которой больше глубина, и у профильно конкурирующих — та, у которой больше широта.

Замена плоскостей проекций

Свойства трехпроекционного чертежа точки позволяют по горизонтальной и фронтальной ее проекциям строить третью на другие плоскости проекций, введенные взамен заданных. На рисунке 65, а показаны точка А и ее проекции — горизонтальная А₁и фронтальная А₂. По условиям задачи необходимо произвести замену плоскостей П₂. Новую плоскость проекции обозначим П₄ и расположим перпендикулярно П₁. На пересечении плоскостей П₁и П₄ получим новую ось П₁/П₄. Новая проекция точки А₄будет расположена налинии связи, проходящей через точку А₁ и перпендикулярно оси П₁/П₄.

Поскольку новая плоскость П₄ заменяет фронтальную плоскость проекции П₂, высота точки А изображается одинаково в натуральную величину и на плоскости П₂, и на плоскости П₄.

Это обстоятельство позволяет определить положение проекции A₄, в системе плоскостей П₁_|_ П₄ (рисунок 65, б) на комплексном чертеже. Для этого достаточно измерить высоту точки на заменяемой плоскости проекции П₂, отложить ее на новой линии связи от новой оси проекций — и новая проекция точки А₄будет построена.

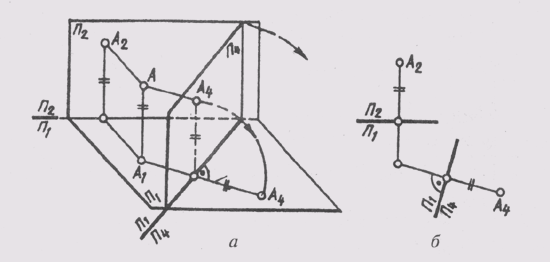
Рисунок 65 – Замена фронтальной плоскости проекций

Если новую плоскость проекций ввести взамен горизонтальной плоскости проекций, т. е. П₄ _|_ П₂ (рисунок 66, а), тогда в новой системе плоскостей новая проекция точки будет находиться на одной линии связи с фронтальной проекцией, причем А₂А₄ _|_. В этом случае глубина точки одинакова и на плоскости П₁, и на плоскости П₄. На этом основании строят А₄ (рисунок 66, б) на линии связи А₂А₄на таком расстоянии от новой оси П₁/П₄ на каком А₁находится от оси П₂/П₁.

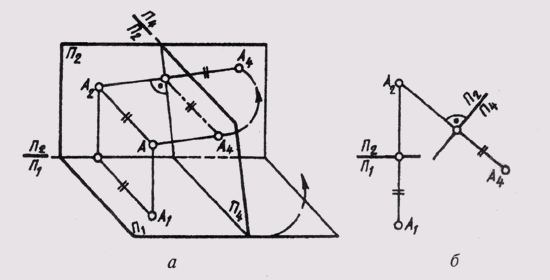
Рисунок 66 - Замена горизонтальной плоскости проекций

Как уже отмечалось, построение новых дополнительных проекций всегда связано с конкретными задачами. В дальнейшем будет рассмотрен ряд метрических и позиционных задач, решаемых с применением метода замены плоскостей проекций. В задачах, где введение одной дополнительной плоскости не даст желаемого результата, вводят еще одну дополнительную плоскость, которую обозначают П₅. Ее располагают перпендикулярно уже введенной плоскости П₄(рисунок 67, а), т. е. П₅П₄ и производят построение, аналогичное ранее рассмотренным. Теперь расстояния измеряют на заменяемой второй из основных плоскостей проекций (на рисунке 67, б на плоскости П₁) и откладывают их на новой линии связи А₄А₅, от новой оси проекций П₅/П₄. В новой системе плоскостей П₄П₅ получают новый двухпроекционный чертеж, состоящий из ортогональных проекций А₄и А₅, связанных линией связи A₄A₅_|_П₄/П₅

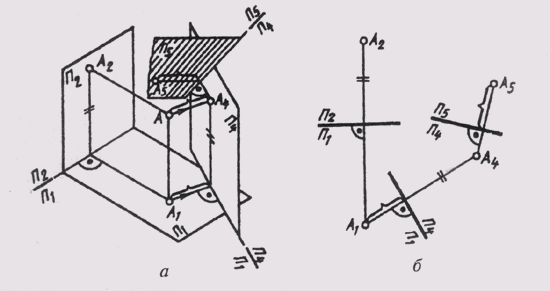
Рисунок 67 – Введение дополнительной плоскости