Олимпиадные задачи ( дистанционные олимпиады
конкурс "Кенгуру", "Математическая карусель")......
ГЛАВА 1: Разные задачи
Задача 1:
В пещере старый пират разложил свои сокровища в 3 цветных сундука, стоящих вдоль стены: в один - драгоценные камни, а в другой - золотые монеты, а в третий - оружие. Он помнит, что :
- красный сундук правее, чем драгоценные камни
- оружие правее, чем красный сундук.
В сундуке какого цвета лежит оружие, если зелёный сундук стоит левее, чем синий?
Решение :
ДК - зелёный
ЗC - красный
О - синий
Задача 2 :
Девять осликов за 3 дня съедают 27 мешков корма.
Сколько корма надо пяти осликам на 5 дней?
Решение :
1 шаг 9 осликов в 1 день - 27 : 3= 9м.
2 шаг 1 ослик в 1 день - 9 : 9 = 1 м.
3 шаг 5 осликов в 1 день - 5 * 1 = 5 м.
4 шаг 5 осликов за 5 дней - 5 * 5 = 25 м.
Задача 3 :
Кенгуру мама прыгает за 1 секунду на 3 метра, а её маленький сынишка прыгает на 1 метр за 0,5 секунды.
Они одновременно стартовали от бассейна к эвкалипту по прямой.
Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров
Решение :
1 шаг 240 : 3 = 80 (с) скакала мама Кенгуру
2 шаг сын за 0,5 с - 1 м, за 1 с - 2 м
3 шаг 80 * 2 = 160 (м) проскачет кенгурёнок за 80 с
4 шаг 240 - 160 = 80 (м) осталось проскакать кенгурёнку когда
мама уже под эвкалиптом
5 шаг 80 : 2 = 40 (с)
Ответ: 40 секунд.
Задача 4 :
На скотном дворе гуляли гуси и поросята.
Мальчик сосчитал количество голов, их оказалось 30, а затем он сосчитал количество ног, их оказалось 84.
сколько гусей и сколько поросят было на школьном дворе?
Решение :
1 шаг Представьте, что все поросята подняли по две ноги вверх
2 шаг на земле осталось стоять 30 * 2 = 60 ног
3 шаг подняли вверх 84 - 60 = 24 ноги
4 шаг подняли 24 : 2 = 12 поросят
5 шаг 30 - 12 = 18 гусей
Ответ: 12 поросят и 18 гусей.
Задача 5
Инженер ежедневно приезжал на станцию в одно и то же время, и в то же время за ним подъезжала машина, на которой он ехал на завод.
Однажды инженер приехал на станцию на 55 мин раньше обычного.
Сразу пошел навстречу машине и приехал на завод на 10 мин раньше, чем обычно.
Во сколько раз скорость инженера меньше скорости машины?
Решение:
За 10 мин машина проходит путь, равный двойному расстоянию от станции до места встречи инженера с машиной.
Значит, путь от станции до места встречи машина проходит за 5 мин.
На месте встречи машина была за 5 мин до времени обычного приезда инженера на станцию, значит, путь от станции до места встречи инженер шел 55 мин - 5 мин = 50 мин.
Следовательно, скорость инженера в 50 : 5 = 10 раз меньше скорости машины.
Задача 6
В триседьмом царстве живут драконы.
У каждого дракона одна, две или три головы,
а) Может ли у 40 % драконов быть 60 % голов?
б) Может ли у 40 % драконов быть 70 % голов?
Решение:
а) Покажем, что у 40% драконов может быть 60% голов.
Пусть в этом царстве живет 100 драконов: 40 драконов с одной головой, 20 – с двумя головами и 40 – с тремя.
Тогда число голов у всех драконов равно
40 • 1 + 20 • 2 + 40 • 3 = 200.
При этом все 40 трехглавых драконов, что составляет 40% от общего числа драконов, имеют 40 • 3 = 120 голов, что составляет
120/200 • 100% = 60% от общего числа голов.
б) Пусть число драконов равно х, а общее число голов у них равно у.
Предположим, что какие-то 40% драконов имеют 70% голов.
Тогда, поскольку каждый из этих драконов имеет не более трех голов, то 0,7у = 3 • 0,4х.
С другой стороны, поскольку остальные 60% драконов имеют 30% голов и у каждого из них не менее одной головы, то 0,6х = 0,3y.
Но эти неравенства не могут выполняться одновременно, так как они равносильны соответственно 7у = 12х и 12x = 6у.
Поэтому у 40% драконов не может быть 70% голов.
Задача 7
В пещере старый пират разложил свои сокровища в 3 цветных сундука, стоящих вдоль стены: в один - драгоценные камни, а в другой - золотые монеты, а в третий - оружие. Он помнит, что :
- красный сундук правее, чем драгоценные камни
- оружие правее, чем красный сундук.
В сундуке какого цвета лежит оружие, если зелёный сундук стоит левее, чем синий?
Решение :
ДК - зелёный
ЗC - красный
О - синий
Задача 8
Девять осликов за 3 дня съедают 27 мешков корма.
Сколько корма надо пяти осликам на 5 дней?
Решение :
1 шаг 9 осликов в 1 день - 27 : 3= 9м.
2 шаг 1 ослик в 1 день - 9 : 9 = 1 м.
3 шаг 5 осликов в 1 день - 5 * 1 = 5 м.
4 шаг 5 осликов за 5 дней - 5 * 5 = 25 м.
Задача 9
Кенгуру мама прыгает за 1 секунду на 3 метра, а её маленький сынишка прыгает на 1 метр за 0,5 секунды.
Они одновременно стартовали от бассейна к эвкалипту по прямой.
Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров
Решение :
1 шаг 240 : 3 = 80 (с) скакала мама Кенгуру
2 шаг сын за 0,5 с - 1 м, за 1 с - 2 м
3 шаг 80 * 2 = 160 (м) проскачет кенгурёнок за 80 с
4 шаг 240 - 160 = 80 (м) осталось проскакать кенгурёнку когда
мама уже под эвкалиптом
5 шаг 80 : 2 = 40 (с)
Ответ: 40 секунд.
Задача 10
На скотном дворе гуляли гуси и поросята.
Мальчик сосчитал количество голов, их оказалось 30, а затем он сосчитал количество ног, их оказалось 84.
сколько гусей и сколько поросят было на школьном дворе?
Решение :
1 шаг Представьте, что все поросята подняли по две ноги вверх
2 шаг на земле осталось стоять 30 * 2 = 60 ног
3 шаг подняли вверх 84 - 60 = 24 ноги
4 шаг подняли 24 : 2 = 12 поросят
5 шаг 30 - 12 = 18 гусей
Ответ: 12 поросят и 18 гусей.
ЗАДАЧА 11
Среди 100 одинаковых на вид монет есть несколько фальшивых. Все фальшивые монеты весят одинаково, все настоящие - тоже, фальшивая монета легче настоящей. Имеются также весы (с двумя чашами без стрелки), на каждой чашке умещается только по одной монете. При этом весы слегка испорчены: если монеты разного веса, перевешивает более тяжёлая монета, а если одинакового - перевесить может любая чашка. Как с помощью этих весов найти хотя бы одну фальшивую монету?
Ответ: Разделим монетки на 33 кучки по 3 монетки + 1 монетка.
Каждое трио взвешиваем между собой, получим 3 неравенства, в результате которых увидим, либо каждая монетка будет по одному разу весить меньше от других двух, либо два раза будет весить меньше других двух.
1>2 (возможны такие варианты: н=н, ф=ф, 2-фальшивка)
1<3 (н=н, ф=ф, 1- фальшивка)
2>3 (н=н, ф=ф, 3- фальшивка)
такое возможно, если все три монетки имеют одинаковый вес вежду собой, то есть из них откладываем в сторонку любую одну
1<2(н=н,ф=ф,1-ф)
1<3(н=н,ф=ф,1-ф)
2>3(н=н,ф=ф,3-ф)
У 1 больше вероятностьть оказаться фальшивой, так что ее и откладываем.
И так проделываем с каждой из 33-х кучек, в результате отложим 11 монет +1, которая не попала ни в одну из кучек.
Эти 12 монет опять разделям на 4 кучки по 3 монетки, проделываем те же манипуляции, в результате получим 4 монетки, разделяем на 1 кучку+1, та монетка из кучки, которая окажется легче, вновь откладываем и сравниваем с одинокой монеткой. Та, которая легче и будет фальшивой.
ГЛАВА П Метод графов
Один из способов решения задач типа «Кто есть кто?» - метод графов.
Граф– это несколько точек, часть которых соединены друг с другом отрезками или стрелками (в этом случае граф называется ориентированным).
Рассмотрим метод графов на примере решения задачи:
Жила-была одна дружная семья: мама, папа и сын. Они все любили делать вместе. Но вот мультфильмы любили разные: «Ну, погоди!», «Покемоны», «Том и Джерри». Определите, какой мультфильм любит каждый из них, если мама, папа и любитель мультфильма «Покемоны» никогда не унывают, а папа и любитель мультфильма «Том и Джерри» делают зарядку по утрам?
Решение:
Рассмотрим множество людей: мама, папа, сын и множество мультфильмов «Ну, погоди!», «Покемоны», «Том и Джерри». Обозначим элементы этих двух множеств точками:
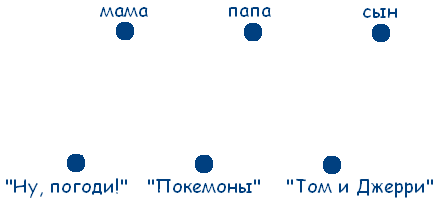
Если точке из одного множества соответствует точка другого множества, будем соединять эти точки сплошной линией, если не соответствует – то штриховой.
Заметим, что по условию задачи у человека только один любимый мультфильм.
Учитывая данные задачи, получаем следующую схему:
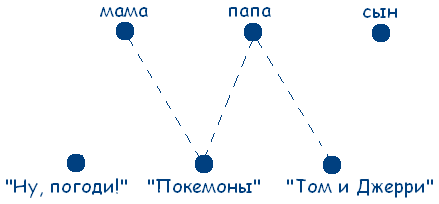
Из условия задачи следует, что нужно найти единственно возможное соответствие между элементами двух множеств.
Правило: если какая-то точка оказывается соединенной с двумя точками другого множества штриховыми линиями, то с третьей точкой она должна быть соединена сплошной.
Поэтому граф на рисунке будет выглядеть следующим образом:
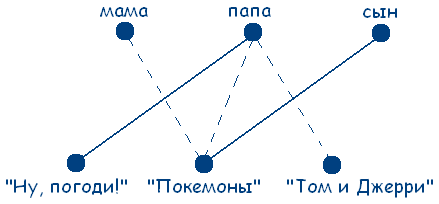
Теперь мы установили, что папа любит мультфильм «Ну, погоди!», сын – «Покемоны». В обеих множествах остается только по одной точке, следовательно мама любит мультфильм «Том и Джерри». Задача решена.
Таким же способом можно находить соответствие между тремя множествами. Тогда при решении мы можем получить треугольники трех видов:
а) все стороны являются сплошными отрезками (решение задачи);
б) одна сторона – сплошной отрезок, а две другие – штриховые;
в) все стороны – штриховые отрезки.
Таким образом, нельзя получить треугольник, у которого бы две стороны были сплошными отрезками, а третья – штриховой отрезок.
Примеры задач:
Задача №1: "Пепси", "Кока-Кола", квас и "Спрайт":
В бутылке, стакане, кувшине и банке находятся «Пепси», «Кока-кола», квас и «Спрайт». Известно, что «Спрайт» и «Пепси» не в бутылке, сосуд с «Кока-колой» находится между кувшином и сосудом с квасом, в банке – не «Кока-кола» и не «Спрайт». Стакан находится около банки и сосуда с «Пепси». Как распределены эти жидкости по сосудам?
Решение:
Из условий задачи получаем таблицу с запретами:
| Сосуд | Бутылка | Стакан | Кувшин | Банка |
| Жидкость | ||||
| «Пепси» | - | - | - | |
| «Кока-кола» | - | - | ||
| Квас | ||||
| «Спрайт» | - | - |
Так как каждая жидкость находится только в одном сосуде, то в в каждой строчке и каждом столбце может стоять только один «+». Вглянув на таблицу, можно сделать вывод, что «Пепси» в кувшине, а квас в банке. Получаем новую таблицу:
| Сосуд | Бутылка | Стакан | Кувшин | Банка |
| Жидкость | ||||
| «Пепси» | - | - | + | - |
| «Кока-кола» | - | - | ||
| Квас | - | - | - | + |
| «Спрайт» | - | - | - |
Теперь можно сказать, что «Спрайт» в стакане, а «Кока-кола» в бутылке.
Ответ:Квас в банке; «Пепси» в кувшине; «Кока-кола» в бутылке; «Спрайт» в стакане.
Задача №2: Любители музыки:
В клубе «Отдых» познакомились 3 любителя клубной музыки видов техно, хаус, рейв. Один говорит: «Вы какую музыку больше любите? Я техно люблю!». Другой ответил, что любит хаус, а третий сказал, что не любит ни техно, ни хаус, но зато обожает рейв. Интересно то, что все они были в банданах и рубашках черного, белого и желтого цветов, но цвет банданы и рубашки совпадал только у любителя техно. А у любителя хаус ни рубашка, ни бандана не были белыми. А любитель рейв был в желтой рубашке. Определите цвет рубашек и бандан каждого из любителей клубной музыки.
Решение:
Заметим, что по условию задачи цвет банданы и рубашки совпадал только у любителя техно. А так как у любителя хаус ни рубашка ни бандана не были белыми и любитель рейв был в желтой рубашке, то делаем вывод, что любитель техно может быть в рубашке и бандане только белого цвета.
Получаем граф:
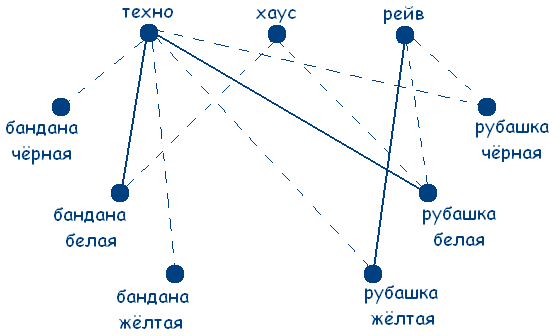
Решение сводится к нахождению трех сплошных треугольников с вершинами в разных множествах. Значит у любителя хаус желтая бандана и черная рубашка (т.к. цвет совпадал только у любителя техно по усл.), а у любителя рейв черная бандана.
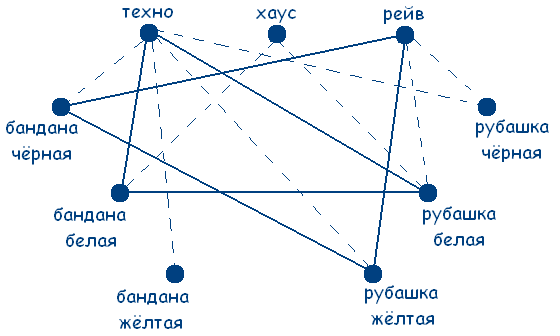
Ответ:У любителя техно рубашка и бандана белого цвета; у любителя хаус черная рубашка и желтая бандана; у любителя рейв желтая рубашка и черная бандана.
Задача №3: Три поросёнка:
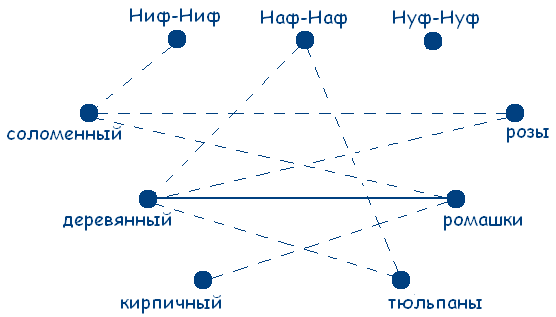
Жили-были на свете три поросёнка, три брата: Ниф-Ниф, Наф-Наф, Нуф-Нуф. Построили они три домика: соломенный, деревянный и кирпичный. Все три брата выращивали возле своих домиков цветы: розы, ромашки и тюльпаны. Известно, что Ниф-Ниф живет не в соломенном домике, а Наф-Наф – не в деревянном; возле соломенного домика растут не розы, а тот, у кого деревянный домик, выращивает ромашки. У Наф-Наф аллергия на тюльпаны, поэтому он не выращивает их. Узнайте, кто в каком домике живет и какие цветы выращивает.
Решение:
Из условий задачи получаем граф:
Можно сделать вывод, что возле кирпичного домика растут розы, а возле соломенного – тюльпаны. А так как Наф-Наф живет не в деревянном домике, то он и не выращивает ромашки. А так как на тюльпаны у него аллергия, то он может выращивать только розы. Внесем эти данные в чертеж и получим:
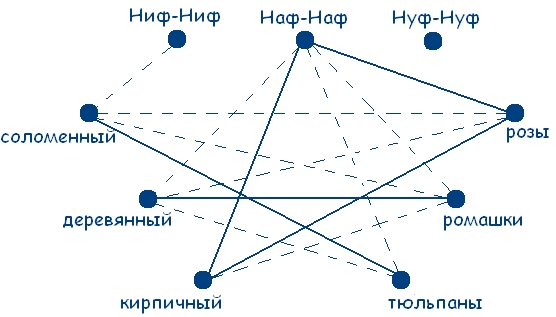
Теперь стало ясно и то, что Ниф-Ниф живет в деревянном домике и выращивает ромашки. Методом исключения получаем, что Нуф-Нуф живет в соломенном домике и выращивает тюльпаны.
Ответ:Наф-Наф живет в кирпичном домике и выращивает розы; Ниф-Ниф живет в деревянном домике и выращивает ромашки; Нуф-Нуф живет в соломенном домике и выращивает тюльпаны.
Задача №4: Компьютерные игры:
В компьютерном классе на уроке информатики, во время отсутствия учителя, пять ребят – Максим, Настя, Саша, Рома, Сережа – отвлеклись от нужной работы и стали играть в такие игры: пасьянс «Паук», гонки, сапер, «Марио», тетрис. Каждый из них играл только в одну игру.
• Саша думал, что в «Марио» играет Настя.
• Настя предполагала, что Рома играет в тетрис, а Максим – в гонки.
• Рома считал, что Сережа играет в гонки, а Саша – в сапера.
• Максим думал, что Настя раскладывает пасьянс «Паук», а в «Марио» играет Рома.
В результате оказалось, что все они ошиблись в своих предположениях. Кто и во что играл?
Решение:
Таблица с известными запретами (исходя из условия задачи):
| Имя | Максим | Настя | Саша | Рома | Сережа |
| Игра | |||||
| Пасьянс «Паук» | - | - | |||
| Гонки | - | - | - | - | |
| Сапер | - | - | |||
| «Марио» | - | - | - | - | |
| тетрис | - | - |
Известно, что каждый из игравших играл только в одну, значит, в каждой строке и каждом столбце таблицы может стоять только один «+».
Из условий задачи следует, что Саша не играл в «Марио»; Настя не играла ни в тетрис, ни в гонки; Рома – ни в гонки, ни в сапера; Максим – ни в пасьянс «Паук», ни в Марио.
Так как все предположения ошибочны, то Настя не играет в «Марио», Рома – в тетрис, Максим – в гонки, Сережа – в гонки, Саша – в сапера, Настя – в пасьянс «Паук», Рома – в «Марио».
Используем правило, что если в строке (или столбце) все места, кроме одного, заняты элементарным запретом (знак несоответствия, например «-»), то на свободное место нужно поставить знак «+». В строчке «гонки» можно поставить «+» напротив имени Саша, а в строчке «Марио» напротив имени Сережа. Получаем:
| Имя | Максим | Настя | Саша | Рома | Сережа |
| Игра | |||||
| Пасьянс «Паук» | - | - | - | - | |
| Гонки | - | - | + | - | - |
| Сапер | - | - | - | ||
| «Марио» | - | - | - | - | + |
| тетрис | - | - | - | - |
Теперь становится ясно, что в пасьянс «Паук» играл Рома, в сапера – Настя, а в тетрис – Максим. Задача решена.
Ответ: Сережа играл в «Марио»; Рома – в пасьянс «Паук»; Саша – в гонки; Настя – в сапера; Максим – в тетрис.
Задача №5: Мушкетёры:
Атос, Портос, Арамис и Д’Артаньян – четыре талантливых молодых мушкетёра. Один из них лучше всех сражается на шпагах, другой не имеет равных в рукопашном бою, третий лучше всех танцует на балах, четвертый без промаха стреляет с пистолетов. О них известно следующее:
• Атос и Арамис наблюдали на балу за их другом – прекрасным танцором.
• Портос и лучший стрелок вчера с восхищением следили за боем рукопашника.
• Стрелок хочет пригласить в гости Атоса.
• Портос был очень большой комплекции, поэтому танцы были не его стихией.
Кто чем занимается?
Решение:
Таблица с известными запретами:
| Занятие | шпажист | рукопашник | танцор | стрелок |
| Имя | ||||
| Атос | - | - | ||
| Портос | - | - | - | |
| Арамис | - | |||
| Д’Артаньян |
Известно, что каждый из четырех мушкетеров был лучшим только в одном деле. Следовательно, в каждой строчке и каждом столбце может стоять только один «+». Взглянув на таблицу, сразу можно сказать, что танцор – Д’Артаньян, шпажист – Портос. Вносим эти данные в таблицу. Получаем:
| Занятие | шпажист | рукопашник | танцор | стрелок |
| Имя | ||||
| Атос | - | - | - | |
| Портос | + | - | - | - |
| Арамис | - | - | ||
| Д’Артаньян | - | - | + | - |
Теперь можно сделать вывод, что стрелок – это Арамис, рукопашник – Атос.
Ответ: Арамис – стрелок; Д’Артаньян – танцор; Портос – шпажист; Атос – рукопашник.
ГЛАВА Ш Табличный способ
Табличный способ решения логических задач также прост и нагляден, но его можно использовать только в том случае, когда требуется установить соответствие между двумя множествами. Он более удобен, когда множества имеют по пять-шесть элементов. Рассмотрим табличный способ на примере решения задачи.
Рассмотрим табличный способ на примере решения задачи:
Четыре футбольных команды: итальянская команда «Милан», испанская – «Реал», российская – «Зенит», английская – «Челси» встретились в групповом этапе лиги чемпионов по футболу. Их тренировали тренеры из этих же четырех стран: итальянец Антонио, испанец Родриго, русский Николай, англичанин Джон. Известно, что национальность у всех четырех тренеров не совпадала с национальностью команд. Требуется определить тренера каждой команды, если известно:
а) Зенит не тренируется у Джона и Антонио.
б) Милан обещал никогда не брать Джона главным тренером.
Решение:
Решая задачу, мы заведомо знаем, что у каждой команды только один тренер.
Чтобы решить задачу табличным способом, нужно знать следующие правила:
1.В каждой строке и в каждом столбце таблицы может стоять только один знак соответствия (например «+»).
2.Если в строке (или столбце) все «места», кроме одного, заняты элементарным запретом (знак несоответствия, например «-»), то на свободное место нужно поставить знак «+»; если в строке (или столбце) уже есть знак «+», то все остальные места должны быть заняты знаком «-».
Таким образом, решение будет доведено до конца, когда мы сумеем разместить по одному плюсу в каждом ряду и колонке, обозначив таким образом, тренеров всех четырех команд.
А теперь приступаем к решению задачи.
Нам известно, что ни у одной из команд национальность тренера и команды не совпадали, а также, что «Зенит» не тренируется у Джона и Антонио, значит у этой команды тренер не Джон и не Антонио; а «Милан» обещал никогда не брать Джона тренером, значит у команды «Милан» тренер не Джон. Если проставить соответствующие минусы, то таблица будет выглядеть так:
| Команда | Италия – «Милан» | Испания – «Реал» | Россия – «Зенит» | Англия – «Челси» |
| Тренер | ||||
| Итальянец Антонио | - | - | ||
| Испанец Родриго | - | |||
| Русский Николай | - | |||
| Англичанин Джон | - | - | - |
Таким образом, становится ясно, что у «Зенита» тренер Родриго (методом исключения). Поставим «+» напротив Родриго в колонке «Зенит» и заполним свободные клетки в его ряду минусами:
| Команда | Италия – «Милан» | Испания – «Реал» | Россия – «Зенит» | Англия – «Челси» |
| Тренер | ||||
| Итальянец Антонио | - | - | ||
| Испанец Родриго | - | - | + | - |
| Русский Николай | - | |||
| Англичанин Джон | - | - | - |
Теперь можно сделать вывод, что тренер «Милана» – Николай. Поставим «+» напротив Николая и заполним свободные клетки в его ряду минусами. Теперь видно, что «Челси» тренирует Антонио, а «Реал» - Джон.
Ответ:
Российская команда «Зенит» тренируется у испанца Родриго; итальянская команда «Милан» тренируется у русского Николая; английская команда «Челси» тренируется у итальянца Антонио; испанская команда «Реал» тренируется у англичанина Марка.
ГЛАВА 1V Задачи на переливание
Рассмотрим еще один тип логических задач. Это задачи на переливания, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости.
Все задачи на переливание можно представить двумя типами:
1. «Водолей» - задачи, в которых необходимо получить некоторое количество жидкости с помощью нескольких пустых емкостей из бесконечного источника, из которого можно наливать жидкость, и в который ее можно выливать.
2. «Переливашка» - задачи, в которых необходимо разделить жидкость в большей емкости с помощью нескольких меньших по объему емкостей, жидкость можно только переливать из одной емкости в другую;
Более систематический подход к решению задач «на переливание» заключается в использовании определённой последовательности действий.
В задачах на переливание разрешены следующие операции:
- заполнение жидкостью одного сосуда до краев;
- переливание жидкости в другой сосуд или выливание жидкости;
При решении таких задач необходимо учитывать следующие замечания:
- разрешается наливать в сосуд ровно столько жидкости, сколько в нем помещается;
- разрешается переливать всю жидкость из одного сосуда в другой, если она в него вся помещается;
- разрешается отливать из одного сосуда в другой столько жидкости, сколько необходимо, чтобы второй сосуд стал полным.
Каждую задачу на переливание таким методом можно решать двумя способами:
I. начать переливания с большего сосуда;
II. начать переливания с меньшего сосуда.
Какой из способов более рационален (т.е. каким способом мы быстрее получим нужное количество жидкости) зависит от условий задачи. Изначально это определить нельзя.
- При решении задач первого типа («Водолей») можно использовать такой алгоритм. Запишите этот алгоритм в карточку для индивидуальной работы (Приложение 1).
Алгоритм I.
- Наполнить большую емкость жидкостью из бесконечного источника.
- Перелить из большей емкости в меньшую емкость.
- Вылить жидкость из меньшей емкости.
- Повторить действия 1-3 до тех пор, пока не будет получено обозначенное в условии задачи количество жидкости.
- При решении задач второго типа («Переливашка») можно использовать следующий алгоритм. Запишите этот алгоритм в карточку для индивидуальной работы (Приложение 1).
Алгоритм II.
- Из большей емкости наполнить емкость промежуточного объема.
- Перелить жидкость из промежуточной емкости в самую маленькую емкость.
- Перелить жидкость из самой маленькой емкости в большую емкость.
- Повторять действия 2-3 до тех пор, пока емкость промежуточного объема не станет пустой.
- Если емкость промежуточного объема опустела, то повторить действия 1-5 до тех пор, пока не будет получено обозначенное в условии задачи количество жидкости.
ЗАДАЧА Даны 2 кувшина вместимостью 8 и 5 литров. Имеется кран с водой и мойка для слива воды. Как с помощью этих двух кувшинов отмерить ровно 6 литров воды?

Задачу можно оформить в виде следующей таблицы:
| 8 л. (А) | 0 л. | 8 л. | 3 л. | 3 л. | 0 л. | 8 л. | 6 л. | 6 л. |
| 5 л. (B) | 0 л. | 0 л. | 5 л. | 0 л. | 3 л. | 3 л. | 5 л. | 0 л. |
