Признаки равенства прямоугольных треугольников. Доказательство одного из них.

Билет № 14

Признаки равенства прямоугольных треугольников. Доказательство одного из них.

Существует четыре признака равенства прямоугольных треугольников:

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны. (АС=А₁С₁, ВС=В₁С₁ )

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны. (например, АС=А₁С₁, ÐА=ÐА₁)

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны. (например, АВ= A₁B₁, ÐА=ÐА₁)

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны. (например, АВ= A₁B₁, АС=А₁С₁)

Докажем признак по гипотенузе и острому углу.

Многоугольник. Элементы многоугольника. Виды многоугольников. Сумма углов выпуклого многоугольника.

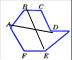Рассмотрим фигуру, составленную из отрезков АВ, ВС, CD, ..., EF, FA так, что смежные отрезки (т. е. отрезки АВ и ВС, ВС и CD, ..., FA и АВ) не лежат на одной прямой, а несмежные отрезки не имеют общих точек. Такая фигура называется многоугольником. Точки А, В, С, ..., Е, F называются вершинами, а отрезки АВ, ВС, CD, ..., EF, FA— сторонами многоугольника.

Сумма длин всех сторон называется периметром многоугольника.

Многоугольник с п вершинами называется п-угольником.

Две вершины многоугольника, принадлежащие одной стороне, называются соседними. Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.

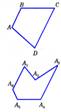Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая — внешней областью многоугольника.

Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. (Многоугольник ABCD – выпуклый, остальные не выпуклые)

Сумма углов выпуклого п-угольника равна (п—2) 180°.

Следствия: 1)Сумма углов любого треугольника равна 180⁰

2) Сумма углов любого четырехугольника равна 360⁰

Билет № 15

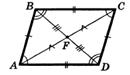
Доказать одно из свойств параллелограмма.

1°. В параллелограмме противоположные стороны равны и противоположные углы равны.

2°. Диагонали параллелограмма точкой пересечения делятся пополам.

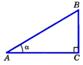
Теорема Пифагора.

Теорема:В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Справедлива теорема, обратная теореме Пифагора

Теорема: Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.

С помощью этой теоремы, зная стороны треугольника, можно определять, является ли он прямоугольным

2. Синус, косинус, тангенс острого угла прямоугольного треугольника. Значения синуса, косинуса, тангенса и котангенса 30⁰, 45⁰, 60⁰.

Определение: Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.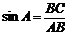

Определение: Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.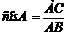

Определение: Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.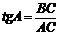

	300	450	600
Sin A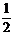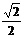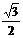
Cos A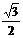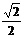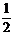
Tg A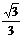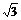

Билет № 17

Билет № 18

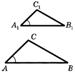1. Третий признак подобия треугольников.

теорема: Если 3 стороны одного треугольника пропорциональны 3 сторонам другого, то такие треугольники подобны.

Билет № 14

Признаки равенства прямоугольных треугольников. Доказательство одного из них.

Существует четыре признака равенства прямоугольных треугольников:

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны. (АС=А₁С₁, ВС=В₁С₁ )

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны. (например, АС=А₁С₁, ÐА=ÐА₁)

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны. (например, АВ= A₁B₁, ÐА=ÐА₁)

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны. (например, АВ= A₁B₁, АС=А₁С₁)

Докажем признак по гипотенузе и острому углу.