Плоскости частного положения.

ЛЕКЦИЯ №3

Плоскости частного положения.

5. плоскости общего положения. способы задания плоскости на чертеже.

Взаимопринадлежность точки, прямой и плоскости.

Плоскости частного положения

В зависимости от расположения относительно плоскостей проекций различают плоскости частного положения и плоскости общего вида. Под «частным» понимают такое расположение плоскостей, когда они параллельны или перпендикулярны плоскостям проекций.

Плоскости, параллельные плоскостям проекций называются плоскостями уровня.

Плоскости перпендикулярные плоскостям проекций, и поэтому проецирующиеся на них в виде прямой линии, называют проецирующими плоскостями.

Фронтальная плоскость Ф

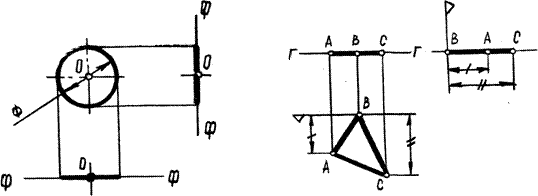Это плоскость параллельная фронтальной плоскости проекций(рисунок 3-1).

Всякая плоская фигура, лежащая в этой плоскости, на виде спереди проецируется в натуральную величину, а на виде сверху и слева - как отрезки прямой совпадающие с проекциями плоскости.

Рисунок 3-1 Рисунок 3-2

Горизонтальная плоскость Г

Это плоскость параллельная горизонтальной плоскости проекций.

Всякая плоская фигура, лежащая в этой плоскости, на виде сверху изображается в натуральную величину (рисунок 3-2), а на видах спереди и слева – как отрезки прямой совпадающие с проекциями самой горизонтальной плоскости.

Профильная плоскость П

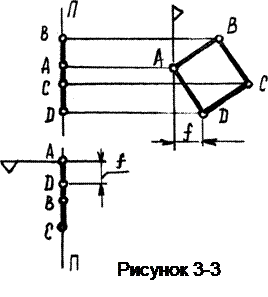Это плоскость параллельная профильной плоскости проекций. Всякая плоская фигура, лежащая в этой плоскости, на виде слева изображается в натуральную величину, а на видах спереди и сверху - как отрезки прямой, совпадающие с проекциями самой плоскости (рисунок 3-3).

Вертикальная плоскость

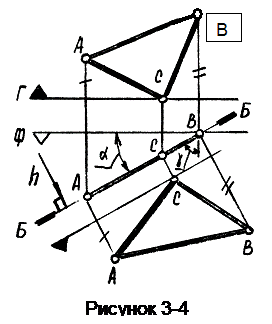Эта плоскость перпендикулярна горизонтальной плоскости уровня (рисунок 3-4).

На виде сверху такая плоскость изображается в виде прямой линии, т.е. имеет вырожденный вид. На виде спереди она занимает всю плоскость проекций, a - угол наклона плоскости Б к фронтальной, а b- к профильной плоскости проекций. Если в плоскости Б взять произвольную фигуру(D АВС), то на виде сверху ее изображение совпадет с изображением плоскости; на виде спереди изображение треугольника будет искажено.

Чтобы определить натуральную величину фигуры, необходимо построить дополнительный вид на плоскость параллельную заданной плоскости Б (или, что то же, по направлению горизонтали h , как прямой перпендикулярной плоскости Б). При таком преобразовании чертежа сохраняются высоты точек.

Наклонная плоскость

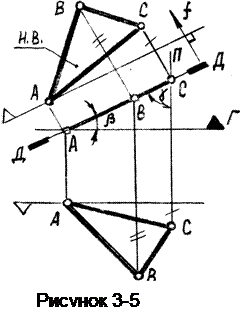Это плоскость перпендикулярная фронтальной плоскости. Д^Ф (рисунок 3-5).Название плоскости определяется ее положением относительно горизонтальной плоскости.

На виде спереди плоскость изображается как прямая, а на виде сверху занимает всю плоскость проекций.

Положение плоскости Д относительно других плоскостей уровня определяется углами b и g.

Изображение любой плоской фигуры лежащей в плоскости Д (например DАВС) на виде спереди совпадает с изображением плоскости, а на виде сверху размеры и форма фигуры изображаются с искажением.

Для определения натуральной величины DАВС следует построить дополнительный вид на плоскость, параллельную заданной плоскости Д (или по направлению прямой перпендикулярной заданной плоскости Д - фронтали f).

В этом случае сохраняются (при построении дополнительного вида) глубины точек фигуры. Базы отсчета глубин проводят; на виде сверху -через дальнюю точку фигуры, на дополнительном виде - в любом удобном месте перпендикулярно новым линиям связи. Новые линии связи проводятся параллельно новому направлению проецирования.

6.6 Плоскость перпендикулярная профильной плоскости проекций

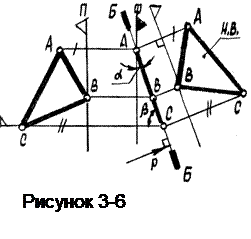
Эта плоскость на виде слева изображается в виде прямой, а на виде спереди занимает всю плоскость проекций. Б^П (рисунок 3-6).

Фигура, лежащая в плоскости Б на виде слева совпадает с изображением плоскости, а на виде спереди изображается с искажением размеров и формы.

Для определения натуральной величины фигуры строим дополнительный вид на плоскость параллельную заданной плоскости Б (или по направлению профильной прямой р перпендикулярной заданной плоскости Б ).

При построении дополнительного вида здесь сохраняются широты точек. Положение плоскости Б относительно других плоскостей уровня определяется углами a и b.

Плоскости общего положения

ЛЕКЦИЯ №4

Таким образом если, имея комплексный чертеж отрезка, мы сумеем построить прямоугольный треугольник катетами которого будут –1)одна из проекций отрезка и 2)разность измерений концов отрезка, отмеряемых от соответствующей первому катету плоскости проекций (от Г- высот, от Ф - глубин, от П – широт), то гипотенуза полученного треугольника будет равна натуральной величине отрезка.

При этом угол между гипотенузой треугольника и проекцией отрезка равен углу наклона отрезка к плоскости проекций (Г, Ф, или П соответственно), (рисунок 4-2б).

Строить такой прямоугольный треугольник по двум катетам можно в любом удобном месте чертежа.

Пример 1.Определить угол наклона отрезка АВ к фронтальной плоскости (рисунок 4-3).

Для определения указанного угла удобно построить прямоугольный треугольник, приняв фронтальную проекцию отрезка в качестве его первого катета. Вторым катетом треугольника в этом случае будет разность глубин концов отрезка измеренная на горизонтальной проекции (виде сверху).

Угол α между первым катетом и гипотенузой и будет искомым. Попутно определится и длина отрезка равная длине гипотенузы треугольника.

Пример 2. Отложить на проекциях прямой m от точки А отрезок АВ, натуральная величина которого равна 50 мм (рисунок 4-4).Можно предложить такой способ решения задачи. Возьмем на указанной прямой произвольную точку С и определим натуральную величину полученного отрезка АС способом прямоугольного треугольника.

Поскольку на гипотенузе треугольника имеем натуральные длины отрезков, отложим здесь от точки А заданную величину 50 мм. Затем проведем прямую параллельно второму катету треугольника до пересечения с проекцией отрезка АС.

Полученная точка будет являться искомой точкой В. Вторую проекцию точки В находим проецируя точку В на вторую проекцию отрезка.

ЛЕКЦИЯ №3

плоскости частного положения.

5. плоскости общего положения. способы задания плоскости на чертеже.