Пересечение двух плоскостей общего положения

Линия пересечения двух плоскостей – это прямая, принадлежащая как одной, так и другой плоскости. Но положение любой прямой в пространстве определяется положением двух ее точек. Поэтому для построения линии пересечения двух плоскостей надо найти две точки, каждая из которых принадлежит обеим плоскостям.

Итак, даны две плоскости, заданные треугольниками АВС и DEF. Метод сводится к тому, что бы поочередно найти две точки пересечения двух ребер одного треугольника с плоскостью другого.

Рассмотрим поэтапное построение линии пересечения треугольников АВС и DEF (рисунок 57):

– заключим прямую ac во фронтально-проецирующую плоскость и перенесем по линиям связи на горизонтальную проекцию точки пересечения этой плоскости с прямыми deи df – точки 1 и 2;

– на горизонтальной проекции соединим проекции точек 1 и 2 и найдем точку пересечения получившейся линии с горизонтальной проекцией той прямой, которую мы заключали во фронтально-проецирующую плоскость, в этом случае – с прямой AC.Мы получили точку M.

– заключим прямую BС во фронтально-проецирующую плоскость и перенесем по линиям связи на горизонтальную проекцию точки пересечения этой плоскости с прямыми EF и DF– точки 3 и 4.

Рисунок 57 – Пересечение двух плоскостей общего положения

Соединим их горизонтальные проекции и получим точку пересечения этой прямой с прямой ВС – точку N.

– соединив точки M и N мы получим линию пересечения плоскостей заданных треугольниками.

– осталось лишь определить видимость ребер треугольников. Это делается методом конкурирующих точек.

Тема 1.5 Преобразование чертежа заменой плоскостей проекций, вращением и плоскопараллельным перемещением

Решение многих пространственных задач (позиционных и метрических) на эпюре часто усложняется из-за того, что заданные геометрические объекты (оригиналы) расположены произвольно относительно плоскостей проекций и, следовательно, проецируются на эти плоскости в искажённом виде. Задание на эпюре прямых и плоскостей частного положения значительно упрощает решение задач и делает их выполнимым при помощи простейших графических построений.

1.5.1 Метод замены плоскостей проекций (замена одной и двух плоскостей проекций, четыре основные задачи преобразования чертежа)

При решении задач на определение истинной (натуральной) величины отрезка прямой линии, плоской фигуры или наклона их к плоскостям проекций, а также на определение расстояний между точкой и прямой или плоской фигурой значительно упрощается, когда геометрические фигуры занимают частное положение относительно плоскостей проекций.

Для этого существуют различные способы преобразования комплексного чертежа. Каждый из них основан на одном из следующих принципов:

1. На изменении положения плоскостей проекций относительно неподвижных геометрических фигур;

2. На изменении положения заданных геометрических фигур относительно неподвижных плоскостей проекций.

Рассмотрим некоторые из них.

Сущность способа состоит в том, что заданные геометрические фигуры неподвижны в заданной системе плоскостей проекций (П₁ , П₂). Последовательно вводятся новые плоскости проекций (П₄, П₅), относительно которых геометрические фигуры займут частное положение. Новая плоскость проекций выбирается с таким расчетом, чтобы она была перпендикулярной к незаменяемой плоскости проекций.

Большинство задач решается с применением одного или двух последовательных преобразований исходной системы плоскостей проекций. Одновременно можно заменять только одну плоскость проекций П₁ (или П₂), другая плоскость П₂ (или П₁) должна оставаться неизменной.

На рисунке 58 представлено наглядное изображение метода замены плоскостей проекций. Фронтальная плоскость П₂ заменяется на новую фронтальную плоскость П₄. Новые проекции точки А (А₁ А₄), при этом, как видно из рисунка 58, высота точки А осталась прежней.

Необходимо запомнить правило построения новых проекций точек при методе замены:

1. линии связи всегда перпендикулярны новым осям проекций;

2.
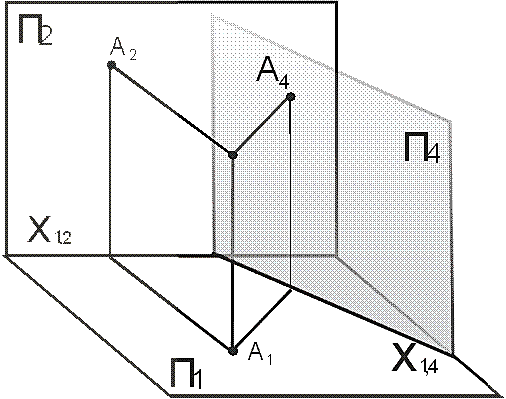
расстояние от новой оси проекций до новой проекции точки всегда берется с той плоскости, которую заменяют.

Рисунок 58 – Наглядное изображение методаРисунок 59 – Метод замены плоскостей

замены плоскостей проекций проекций на эпюре

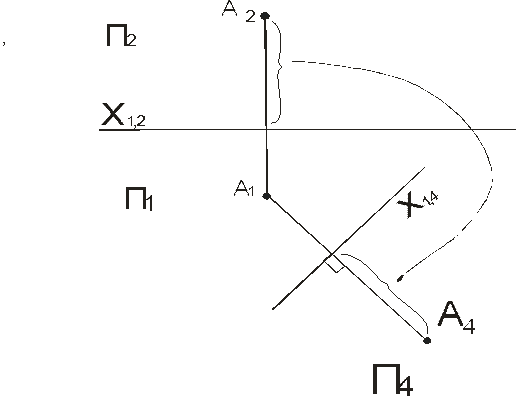
На рисунке 59 изображен метод замены плоскостей проекций на эпюре.

Большинство задач в начертательной геометрии решаются на базе четырех задач:

1. Преобразовать прямую общего положения в прямую уровня.

2. Преобразовать прямую общего положения в проецирующую прямую.

3. Преобразовать плоскость общего положения в проецирующую плоскость.

4. Преобразовать плоскость общего положения в плоскость уровня.

Задача №1.Преобразовать прямую общего положения в прямую уровня.

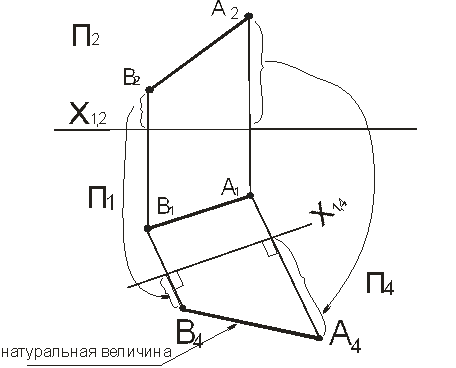
Дана прямая АВ – общего положения, преобразуем ее в прямую уровня (рисунок 60). Для этого вводим новую фронтальную плоскость проекций П₄, ось Х_1,4 проводим параллельно А₁В₁. Строим новую проекцию прямой АВ – А₄В_4. В новой системе плоскостей проекций прямая АВ – фронталь.

Рисунок 60 – Преобразование прямой общего положения в плоскость уровня

Задача №2.Преобразовать прямую общего положения в проецирующую прямую.

Дана прямая АВ – общего положения, преобразуем ее в проецирующую прямую (рисунок 61).

Для решения этой задачи необходимо выполнить последовательно два преобразования:

1. Преобразовать прямую общего положения в прямую уровня, то есть решить сначала задачу №1;

2. Преобразовать прямую уровня в проецирующую прямую.

Вычертить условие задачи №1, самостоятельно решить ее, затем приступить к выполнению второго преобразования. Вводим новую горизонтальную плоскость проекций П₅, для этого проводим новую ось проекций Х₄,₅ перпендикулярно проекции А₄В₄ и строим новую проекцию прямой А₅В_5. В системе плоскостей П₄,П₅, прямая АВ является горизонтально проецирующей прямой.

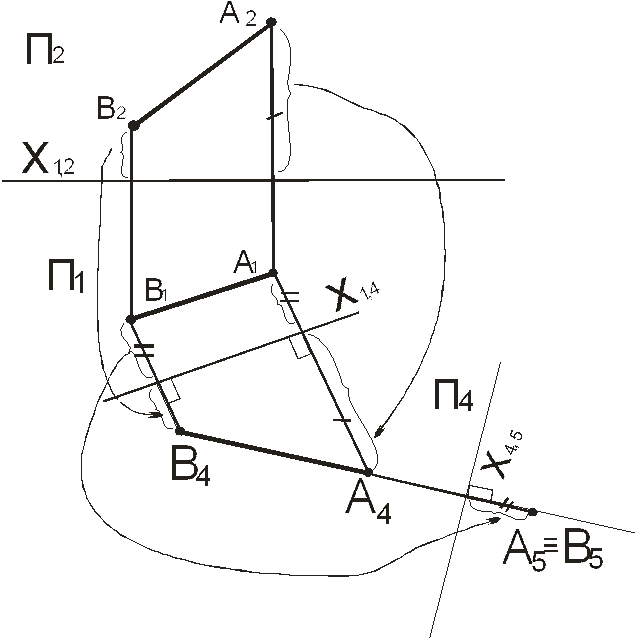
Рисунок 61 – Преобразование прямой общего положения
в проецирующую прямую

Задача №3.Преобразовать плоскость общего положения в проецирующую плоскость.

Дана плоскость АВС – общего положения, преобразуем ее в проецирующую плоскость (рисунок 62). Для решения этой задачи необходимо в плоскости провести линию уровня, если такая отсутствует. Новую ось проекций проводим перпендикулярно линии уровня. В треугольнике АВСпроводим горизонталь h. Ось проекций Х₁₄ проводим перпендикулярно h₁,новую проекцию плоскости А₄В₄С₄, строим по правилам, разобранным в предыдущих задачах.

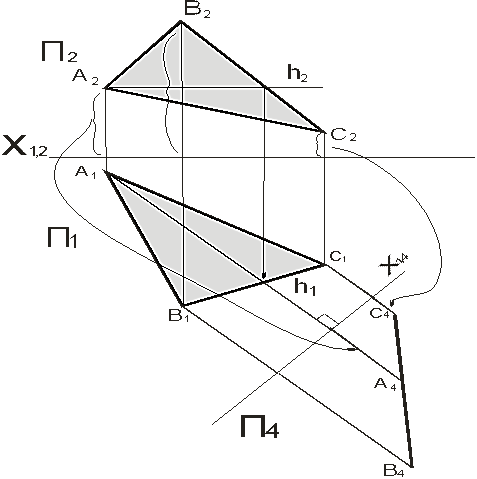
Рисунок 62 – Преобразование прямой общего положения
в проецирующую плоскость

В системе плоскостей проекций П₁,П_4, плоскость треугольника является фронтально-проецирующей плоскостью.

Задача №4.Преобразование плоскости общего положения в плоскость уровня.

Дана плоскость АВС – общего положения, преобразуем ее в плоскость уровня (рисунок 62). Для решения этой задачи необходимо выполнить последовательно два преобразования:

1. Преобразовать плоскость общего положения в проецирующую плоскость, то есть решить сначала задачу №3;

2.
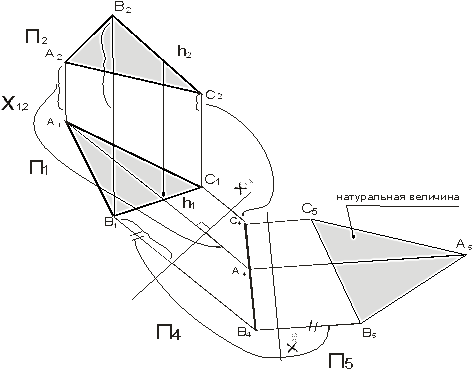
Преобразовать проецирующую плоскость в плоскость уровня.

Вычертить условие задачи №3, самостоятельно решить ее, затем приступить к выполнению второго преобразования. Вводим новую горизонтальную плоскость проекций П₅, для этого проводим новую ось проекций Х₄,₅ параллельно проекции А₄В₄С₄ и строим новую проекцию треугольника А₅В₅С_5. В системе плоскостей П₄,П₅, треугольник АВС является горизонтальной плоскостью уровня.

1.5.2Метод вращения (вращение вокруг проецирующих прямых
и прямых уровня – ось вращения, центр вращения,
радиус вращения, плоскость вращения)