Следует отметить, что выступающие углы треугольника всегда видимые.
Метрические задачи
Положение точки относительно плоскостей проекций.Точка принадлежит плоскости, если проекции точки лежат на соответствующих проекциях прямой, принадлежащих данной плоскости. Если точка лежит в плоскости проекций, то ее проекция на эту плоскость совпадает с самой точкой, а две другие проекции располагаются на осях проекций (рис. 21).
|
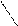
|
Рис. 21. Проекции точек, лежащих на плоскостях проекций
Нахождение натуральной величины треугольника способом перемены плоскостей.Введем две дополнительные плоскости проекций (рис. 22):
1. V1  H и V1
H и V1 
 ABC.
ABC.
2. H1 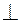 V1 и H1
V1 и H1 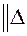 ABC.
ABC.
|
|
|
|
|

|
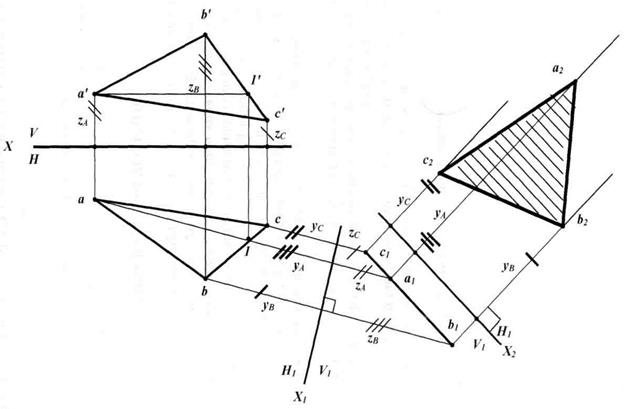
 Рис. 22. Определение натуральной величины треугольника способом перемены плоскостей
Рис. 22. Определение натуральной величины треугольника способом перемены плоскостей
1. Так как V1 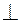 H и V1
H и V1 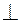
 ABC, то
ABC, то  ABC является проецирующим в плоскости V1. Для построения проекции
ABC является проецирующим в плоскости V1. Для построения проекции  ABC в плоскости V1 построим горизонталь (А1): ее фронтальная проекция (a’1’), горизонтальная проекция (a1).
ABC в плоскости V1 построим горизонталь (А1): ее фронтальная проекция (a’1’), горизонтальная проекция (a1).
2. Перпендикулярно горизонтальной проекции (a1) проведем ось X1 — горизонтальный след плоскости V1.
3. Проведем через точки a, b, c прямые l1, l2, l3 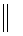 (a1).
(a1).
4. От оси X1 на l1, l2, l3 отложим отрезки zA, zB, zC, которые должны лежать на одной прямой. Отрезок (c1b1) — фронтальная проекция  ABC в плоскости V1.
ABC в плоскости V1.
5. Рассмотрим плоскости H1 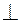 V1 и H1
V1 и H1  ABC, в ней
ABC, в ней  ABC является треугольником уровня и виден в натуральную величину. Проведем ось X2
ABC является треугольником уровня и виден в натуральную величину. Проведем ось X2  (c1b1) — след плоскости H1 в плоскости V1.
(c1b1) — след плоскости H1 в плоскости V1.
6. Проведем через точки a1, b1, c1 прямые n1, n2, n3  X2.
X2.
7. На прямых n1, n2, n3 отложим от оси X2 расстояния yA, yB, yC и получим точки a2, b2, c2.
8.  a2 b2 c2 является натуральной величиной
a2 b2 c2 является натуральной величиной  ABC.
ABC.
Нахождение натуральной величины треугольника способом вращения без указания на чертеже осей вращения, перпендикулярных плоскостям V и H. Порядок построения указан на рис. 23.
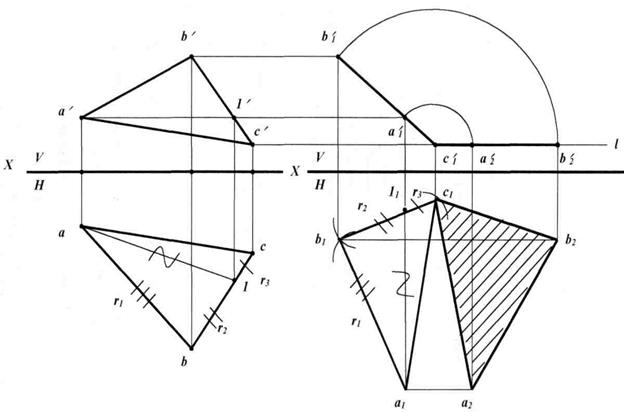
Рис. 23. Определение натуральной величины треугольника методом вращения
Поворот вокруг оси 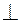 H, проходящей через точку a до положения
H, проходящей через точку a до положения  ABC
ABC 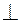 V.
V.
1. В  ABC проводим горизонталь (А1): в
ABC проводим горизонталь (А1): в  a’b’c’ проведем прямую (a’1’)
a’b’c’ проведем прямую (a’1’) 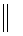 X.
X.
2. В  abc найдем проекцию горизонтали (a1).
abc найдем проекцию горизонтали (a1).
3. На свободном поле чертежа проведем прямую (a111) 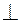 V, или, что то же самое (a111)
V, или, что то же самое (a111) 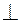 X.
X.
4. От точки a1 сделаем засечку радиусом r1, от точки 11 сделаем засечку радиусом r2 и на пересечении получим точку b1.
5. Проведем прямую через точки b1 и 11 и на ней от точки 11 радиусом r3 получим точку c1.
6. Из точек a’, b’, c’ проведем прямые параллельно оси X, из точек a1, b1, c1 проведем перпендикуляры к оси X, на их пересечении получаем точки a1’, b1’, c1’. Отрезок (b1’ c1’) — фронтальная проекция  ABC.
ABC.
Поворот вокруг оси 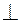 V, проходящей через точку c1 до положения
V, проходящей через точку c1 до положения  ABC
ABC 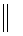 H.
H.
1. Через точку c1’ проведем прямую l 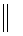 X.
X.
2. Радиусами (c1’a1’), (c1’b1’) сделаем засечки на прямой l и получим точки a2’, b2’.
3. Из точек a2’, b2’, c1’ проведем прямые перпендикулярно X, из точек a1, b1 проведем прямые параллельно X, на их пересечении получим точки a2, b2.
4.  a2 b2 c1 — натуральная величина
a2 b2 c1 — натуральная величина  ABC.
ABC.
Многогранники
Геометрическая поверхность образуется движением в пространстве прямой или кривой линии, называемой образующей, по другой линии (или двум линиям) называемой направляющей. Часть пространства, ограниченная со всех сторон геометрической поверхностью, называется геометрическим телом.
Эпюры многогранников.Многогранником называется геометрическое тело, ограниченное плоскими фигурами — многоугольниками.
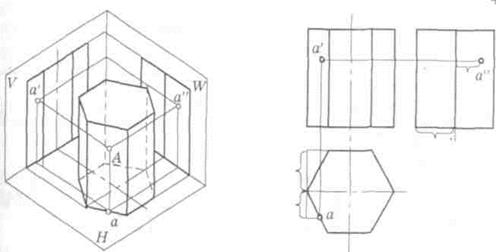 |
Призма — многогранник, две грани которого являются равными многоугольниками, расположенными в параллельных плоскостях (основания призмы), а остальные грани — параллелограммами (боковые грани призмы) — см. рис. 24.
Рис. 24. Эпюры шестигранной призмы
Призма, боковые грани которой перпендикулярны основаниям, называется прямой. Если боковые грани не перпендикулярны основаниям, призма называется наклонной. Боковые грани прямой призмы представляют собой прямоугольники. Если в основании прямой призмы лежит правильный многоугольник, то призма называется правильной. Линии пересечения боковых граней называются боковыми ребрами. Линии пересечения боковых граней с основаниями называются ребрами основания. Точки пересечения ребер называются вершинами призмы.
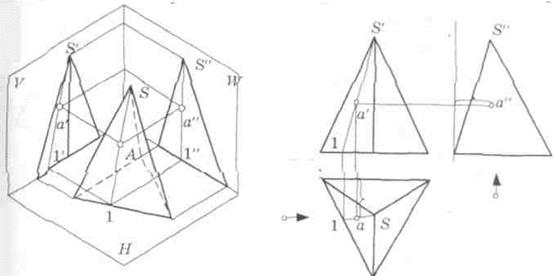 |
Пирамида — многогранник, одна грань которого (основание) является многоугольником, а остальные грани (боковые) — треугольники с общей вершиной (рис. 25).
Рис. 25. Эпюры трехгранной пирамиды
Если в основании пирамиды лежит правильный многоугольник, а высота пирамиды проходит через центр основания (центр описанной вокруг основания окружности), то пирамида называется правильной. Боковыми гранями правильной пирамиды будут равнобедренные треугольники. Боковые ребра пирамиды пересекаются в одной точке, называемой вершиной пирамиды.
Пересечение многогранников.Рассмотрим задачу определения линии пересечения призмы и пирамиды (рис. 26).
1. Найти точки пересечения ребер призмы с гранями пирамиды.
1.1. Так как грани призмы перпендикулярны к плоскости H, то горизонтальные проекции точек пересечения ребер пирамиды с гранями призмы: точки 1 = (as)  (ek), 3 = (bs)
(ek), 3 = (bs)  (ek), 3 = (bs)
(ek), 3 = (bs) 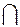 (ed), 4 = (bs)
(ed), 4 = (bs) 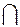 (dk), 5 = (cs)
(dk), 5 = (cs) 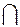 (ed), 6 = (cs)
(ed), 6 = (cs) 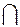 (ek).
(ek).
1.2. Найдем соответствующие фронтальные проекции полученных точек линиями проекционной связи: точки 1’ на (a’s’), 2’ на (a’s’), 3’ на (b’s’), 4’ на (b’s’), 5’ на (c’s’), 6’ на (c’s’).
2. Найти точки пересечения ребер призмы с гранями пирамиды.
2.1. Ребра EE1 и DD1, как видно из чертежа, в пересечении не участвуют.
2.2. Для построения точек пересечения ребра KK1 с гранями пирамиды проведем через ребро KK1 горизонтально-проецирующую плоскость, которая пересекает грань ABS по прямой (MS), грань BCS по прямой (NS): горизонтальный след этой плоскости — прямая (ms,ns), фронтальные проекции этого следа будут на соответствующих плоскостях -— это прямые (m’s’), (n’s’).
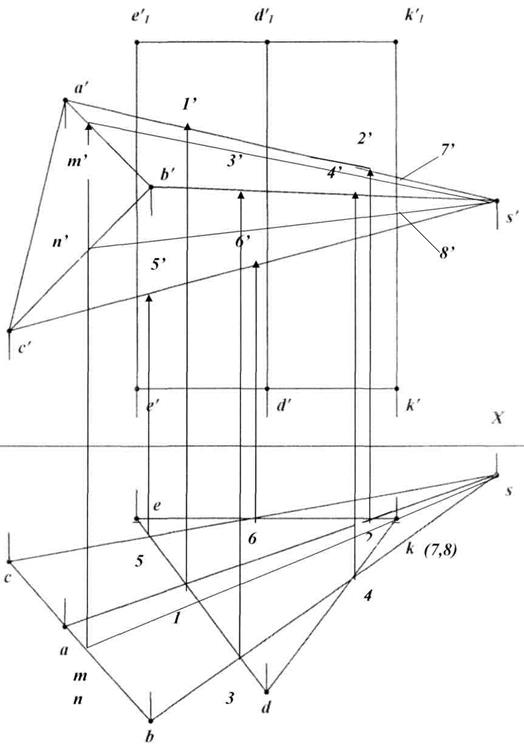 2.3. Фронтальные проекции точек пересечения ребер призмы с гранями пирамиды: точки 7’ = (m’s’)
2.3. Фронтальные проекции точек пересечения ребер призмы с гранями пирамиды: точки 7’ = (m’s’)  (k1’k’), 8’ = (n’s’)
(k1’k’), 8’ = (n’s’)  (k1’k’). Горизонтальные проекции точек пересечения ребер пирамиды с гранями призмы: точки 7 и 8.
(k1’k’). Горизонтальные проекции точек пересечения ребер пирамиды с гранями призмы: точки 7 и 8.
|
В данном случае горизонтальная проекция линии пересечения поверхностей многогранников совпадает с горизонтальной проекцией призмы, и найденные точки следует соединять только на фронтальной проекции. Для определения последовательности соединения фронтальных проекций точек, полученных в пересечении двух многогранников, используют метод Д.Г. Ананова. Он основан на построении схематических разверток поверхностей пересекающихся тел. Ребра призмы на схеме расположены вертикально, ребра пирамиды — наклонно (рис. 27). На развертки наносим точки, принадлежащие линии пересечения. Отметим на схеме знаком «+» те грани, которые на фронтальной плоскости будут видимы, а знаком «-» те грани, которые на этой плоскости будут невидимы. (Линии на гранях, где сочетаются два «минуса», будут невидимы).
Составляем схему соединения точек и видимости линий.
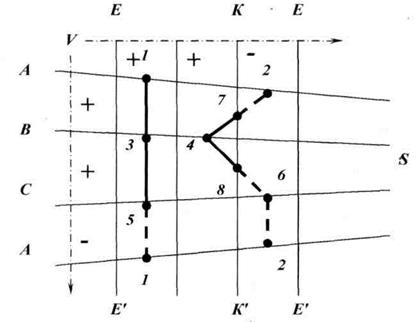 |
Рис. 27. Схема соединения точек и видимости линий
Соединим точки, лежащие на одной грани: точки 1 и 3, 3 и 5, 5 и 1 –— лежат на грани EDE1D1, точки 2 и 7, 7и 4 — лежат на грани ABS, точки 4и 8, 8 и 6 — лежат на грани CBS точки 6 и 2 — лежат на грани ACS.
Определим видимость, используя правило: отрезки, принадлежащие двум видимым граням, — видимы,; отрезки, принадлежащие двум невидимым граням, — невидимы;, отрезки, принадлежащие двум разным по видимости граням, — невидимы.
Отрезки 1-3, 3-5, 7-4, 4-8 — видимы,; отрезки 5-1, 2-7, 8-6, 6-2 — невидимы.
На фронтальной проекции соединим отрезки согласно схеме, видимые отрезки — сплошными основными линиями, невидимые — штриховыми линиями (рис. 28).
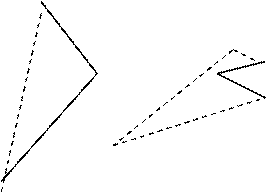 
    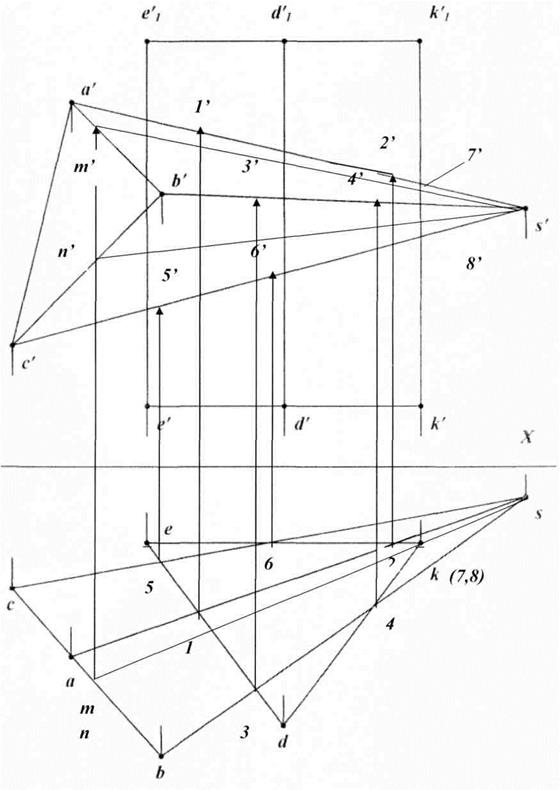 |
Рис. 28. Построение линий пересечения призмы и пирамиды
Тела вращения
Эпюры тел вращения. Поверхность вращения — поверхность, образованная вращением прямой или кривой линии вокруг неподвижной прямой (оси вращения). Если все точки образующей движутся вокруг оси по окружностям, то полученная поверхность называется круговой. Телами вращения называют геометрические тела, ограниченные поверхностями вращения и плоскостями (цилиндр, конус), или только поверхностями вращения (шар, сфера, тор).
Цилиндрической называется поверхность, образованная вращением прямой линии, параллельной оси вращения.
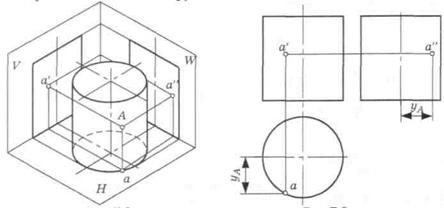 |
Цилиндром называют геометрическое тело, ограниченное круговой цилиндрической поверхностью с двумя параллельными друг другу кругами — основаниями (рис. 29). Если образующие цилиндра перпендикулярны основаниям, то цилиндр называется прямым, если образующие расположены под углом, отличным от 900, то цилиндр называется наклонным.
Рис. 29. Эпюры прямого цилиндра
Коническая поверхность образуется вращением прямой линии, пересекающей ось вращения. Точка пересечения образующей с осью вращения называется вершиной конуса.
Конусом называется геометрическое тело, ограниченное конической круговой поверхностью, расположенной по одну сторону от вершины, и кругом — основанием конуса (рис. 30). Если основание конуса перпендикулярно оси вращения, то конус называется прямым, если основание конуса расположено под углом к оси вращения, то конус называется наклонным.
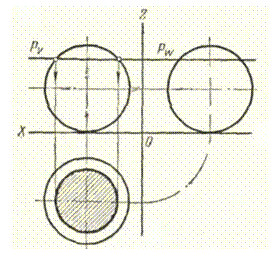
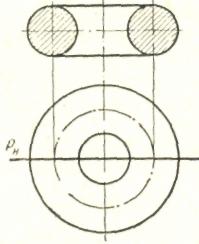
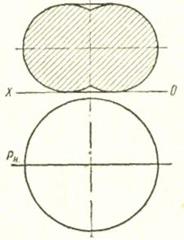
Сферической называется поверхность, образованная вращением окружности вокруг оси, расположенной в плоскости окружности и проходящей через центр окружности. Часть пространства, ограниченная сферической поверхностью, называется шаром (рис. 31). При пересечении сферической поверхности плоскостью всегда получается круг (рис. 32). Круговое кольцо является телом, поверхность которого образована вращением окружности вокруг оси, лежащей в плоскости окружности, но не проходящей через ее центр (рис. 33).
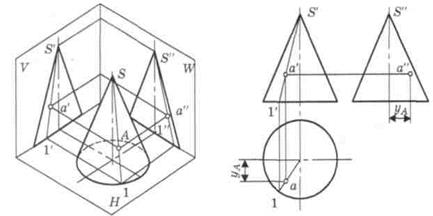 |
Рис. 30. Эпюры прямого конуса
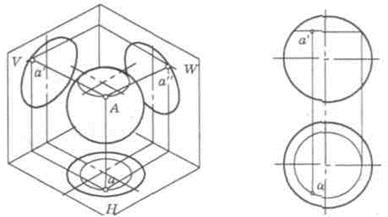 |
Рис. 31. Эпюры сферической поверхности (шара)
 |
| |||
| |||
Рис. 32. Эпюры сечения сферической поверхности плоскостью
 |
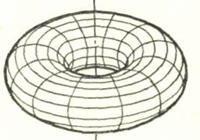 |
Рис. 33. Эпюры кругового кольца и его сечение фронтальной плоскостью
 |
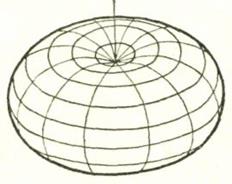 |
Тором называют поверхность вращения, полученную при вращении дуги окружности вокруг замыкающей ее хорды (рис. 34).
Рис. 34. Эпюры тора и его сечение фронтальной плоскостью
Пересечение тел вращения. Пересечение тел вращения рассмотрим на примере пересечения конуса и цилиндра (рис. 35).
1. На фронтальной проекции отметим характерные точки пересечения конуса и цилиндра: точки 1’, 2’, 3’, 4’, 5’, 6’.
2. Найдем горизонтальные проекции этих точек: точки 1, 2, 3, 4, 5, 6. Точка 1 лежит на горизонтальной проекции образующей конуса. Через точку 2’ проведем вспомогательную фронтально-проецирующую плоскость, на плоскости H диаметром (2’21’) проводим окружность и получаем точку 2 на пересечении этой окружности и линии проекционной связи. Аналогично строим точки 3, 4, 5, 6. Точки 3’ (на плоскости H ее проекции 3 и 31) лежат на диаметре (a’b’). Точки 4’ (4 и 41) — на радиусе (4’41’), точки 5’ (5 и 51) — на радиусе от оси конуса до точки 51’ или, что то же самое, на образующей цилиндра, точки 6’ (6 и 61) —-на радиусе (6’61’).


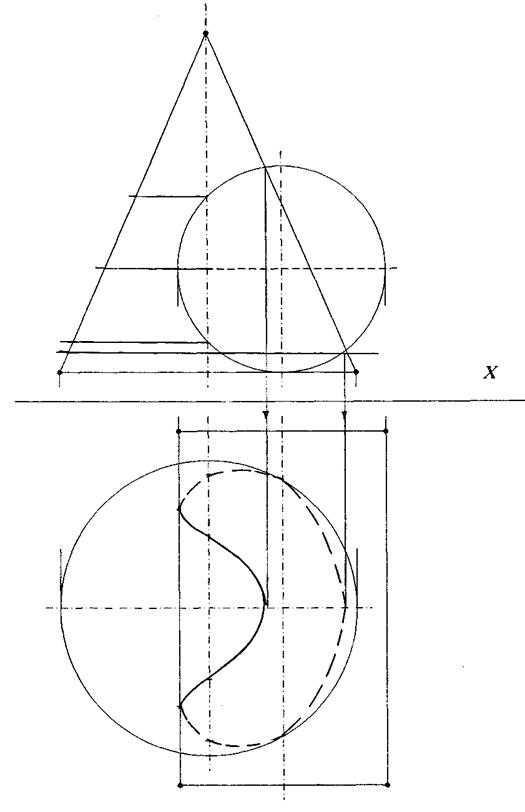 |
3.  Точки 1’, 6’, 5’, лежащие выше оси симметрии цилиндра, — видимые;, точки 2’, 3’, 4’, лежащие ниже оси, — невидимые.
Точки 1’, 6’, 5’, лежащие выше оси симметрии цилиндра, — видимые;, точки 2’, 3’, 4’, лежащие ниже оси, — невидимые.
Аксонометрические проекции
Виды аксонометрических проекций. Для изображения объекта на плоскости используют:
1. Рисунок, который изображает предмет так, как он представляется глазу наблюдателя. В общем случае рисунок искажает форму и размеры предмета.
2. Чертеж из ортогональных проекций. Чертеж дает представление о размерах и форме предмета, но зачастую недостаточно нагляден.
3. Перспективное изображение, основанное на методе центрального проецирования. Оно дает представление о форме объекта, а размеры искажает.
4. Аксонометрические проекции дают наглядное, но несколько искаженное изображение предмета. Чаще всего их строят в дополнение к ортогональным проекциям, чтобы представить пространственную форму сложных объектов.
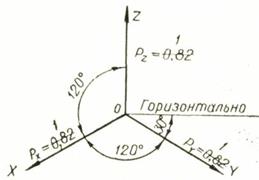
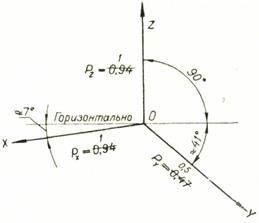
Стандартом установлены пять видов аксонометрических проекций. Прямоугольные аксонометрические проекции (проецирующие линии перпендикулярны аксонометрической плоскости проекций) подразделяются на изометрическую и диметрическую проекции (рис. 36).
Косоугольные аксонометрические проекции (проецирующие линии направлены под углом к аксонометрической плоскости проекций) делятся на фронтальную изометрическую, горизонтальную изометрическую и фронтальную диметрическую проекции (рис. 37).
 |
 |
|
|
Рис. 36. Расположение координатных осей и коэффициенты искажения в прямоугольной изометрии (а) и в прямоугольной диметрии (б)
  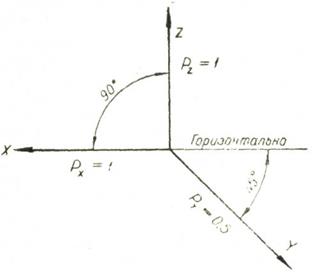 |
Рис. 37. Расположение координатных осей и коэффициенты искажения для косоугольной фронтальной диметрической проекции
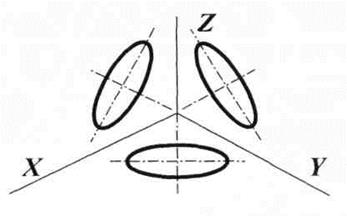
Построение окружности в изометрии. Прямоугольные изометрические проекции наиболее просты и наглядны и чаще всего применяются в начертательной геометрии и черчении. В прямоугольной изометрии окружность изображается в виде эллипса, большая ось эллипса всегда перпендикулярна малой оси эллипса, а малая ось располагается на третьей оси проекции. Эллипсы на плоскостях проекций расположены так, как показано на рис. 38. При построении окружности в изометрии рассчитывают длины большой и малой осей эллипса по формулам:
Dбо = 1,22d
 |
Dмо = 0,71d.
Рис. 38. Расположение эллипсов на плоскостях проекций
Например, для окружности диаметром d = 50 мм: Dбо = 1,22d = 61 мм, Dмо = 0,71d = 35 мм. Последовательность построения эллипса показана на рис. 39.
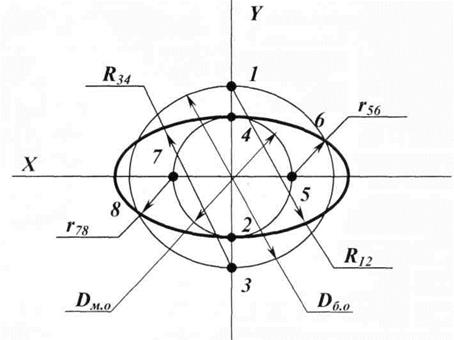 |
Рис. 39. Последовательность построения эллипса
для горизонтальной плоскости проекций
 |
Задачи для самостоятельного решения
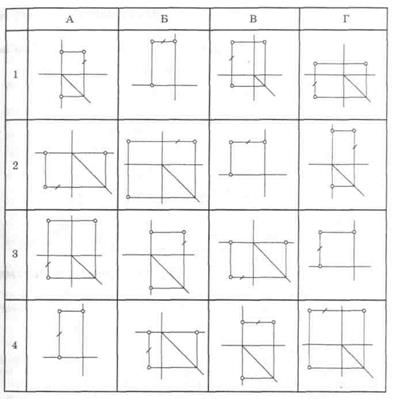
Рис. 40. Проецирование точки
- Какое положение занимает точка относительно плоскостей проекций?
- Расстояние от точки до какой плоскости проекций определяет отрезок, отмеченный засечкой?
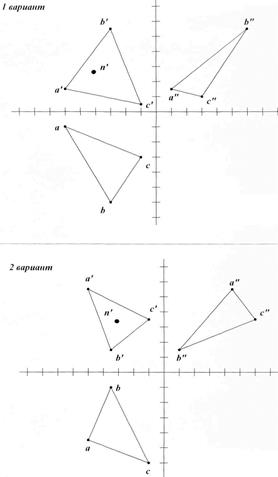 | 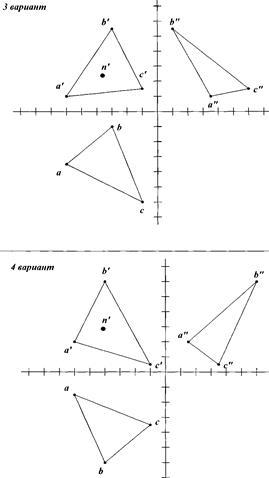 | ||
Рис. 41. Проецирование точки на плоскость
Найти горизонтальную и профильную проекции точки N.
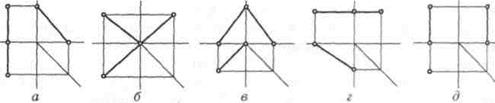 |
Рис. 42. Проецирование прямой линии
1. Какое положение относительно плоскостей проекций занимают отрезки?
2. Каких плоскостей касаются отрезки своими концами?
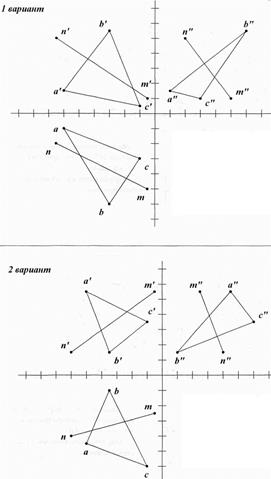 | 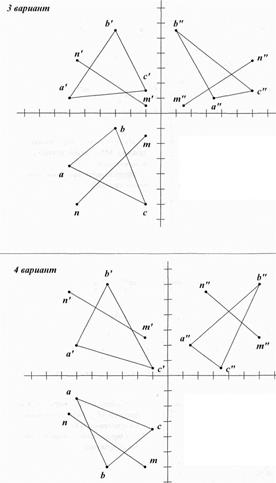 | ||
Рис. 43. Пересечение прямой и плоскости
- Найти точку пересечения прямой MN с непрозрачной плоскостью ABC.
- Определить видимость участков прямой.
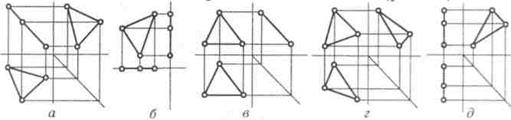 |
Рис. 44. Положение плоской фигуры относительно плоскостей проекций
1. Какое положение относительно плоскостей проекций занимают плоские фигуры?
2. На какие плоскости проекций фигуры проецируются в действительную величину?
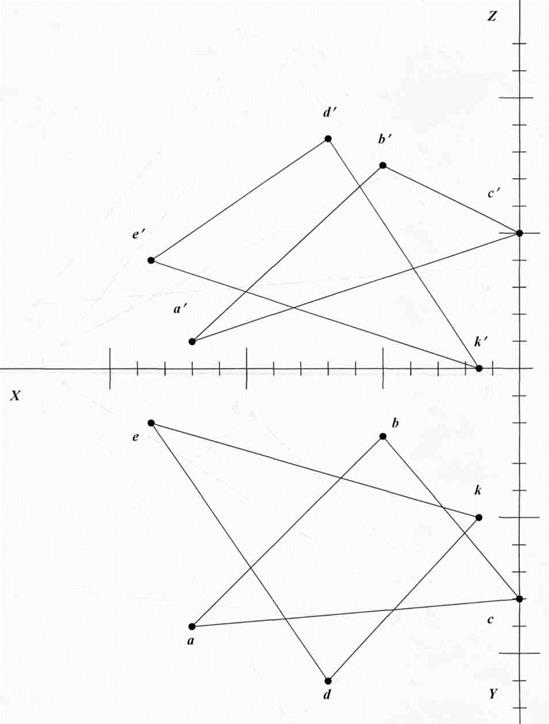 |
Рис. 45. Пересечение плоскостей
- Построить линию пересечения плоскостей, заданных треугольниками ABC и EDK.
- Определить видимость треугольников в проекциях.
- Использовать два варианта:
- провести вспомогательные фронтально-проецирующие плоскости через AB и AC;
- провести вспомогательные фронтально-проецирующие плоскости через DK и EK.
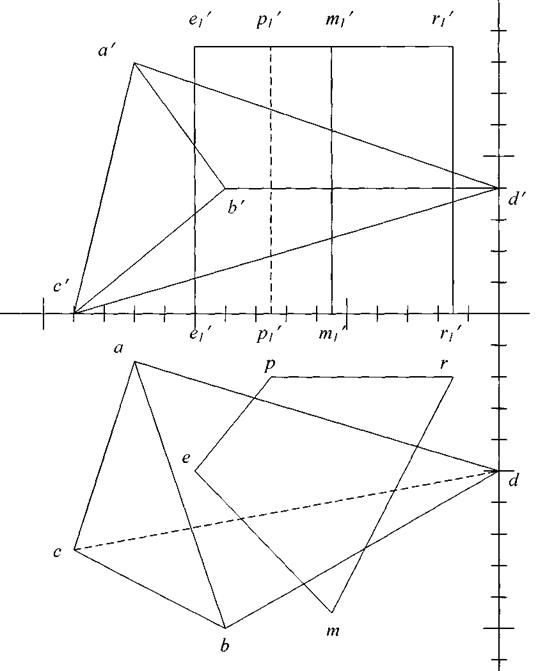 |
Рис. 46. Пересечение многогранников
- Построить линию пересечения пирамиды с прямой призмой.
- Определить видимость участков линии пересечения.
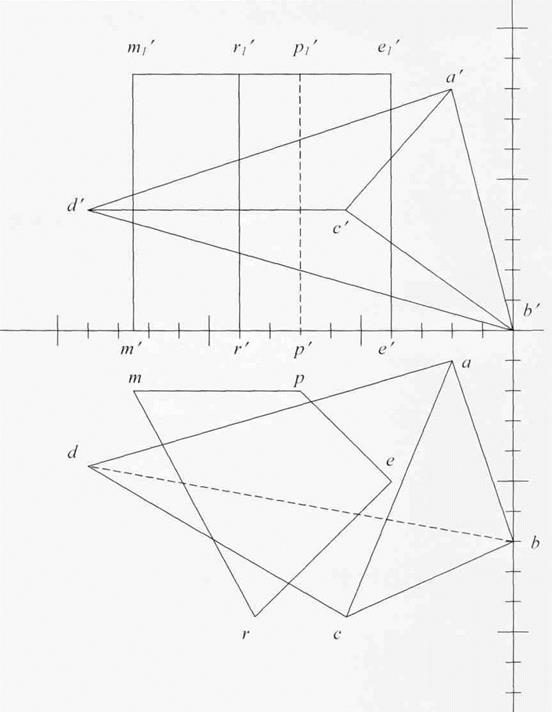 |
Рис. 47. Пересечение многогранников
- Построить линию пересечения пирамиды с прямой призмой.
- Определить видимость участков линии пересечения.
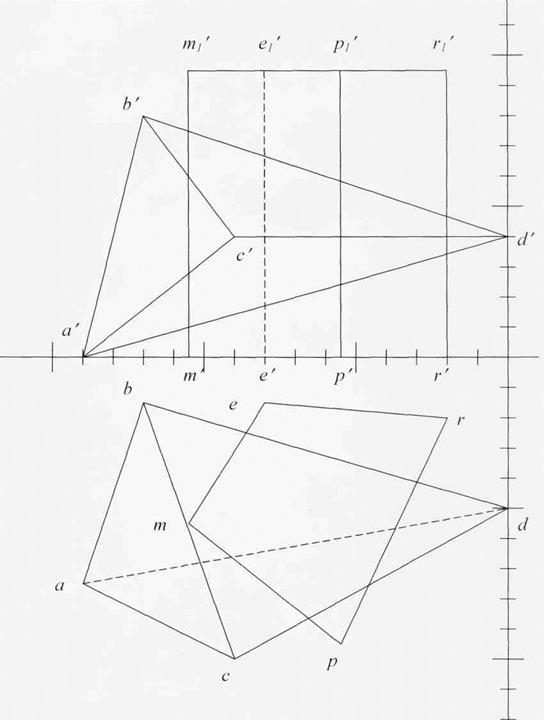 |
Рис. 48. Пересечение многогранников
- Построить линию пересечения пирамиды с прямой призмой.
- Определить видимость участков линии пересечения.
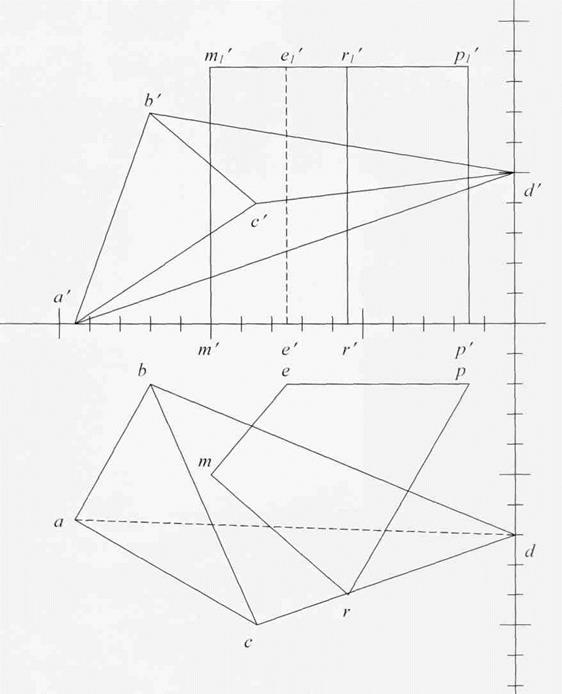 |
Рис. 49. Пересечение многогранников
- Построить линию пересечения пирамиды с прямой призмой.
- Определить видимость участков линии пересечения.
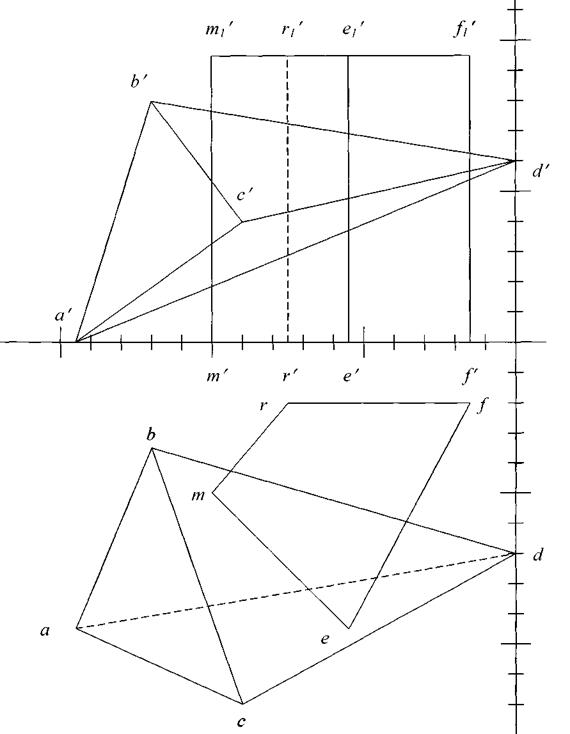 |
Рис. 50. Пересечение многогранников
- Построить линию пересечения пирамиды с прямой призмой.
- Определить видимость участков линии пересечения.
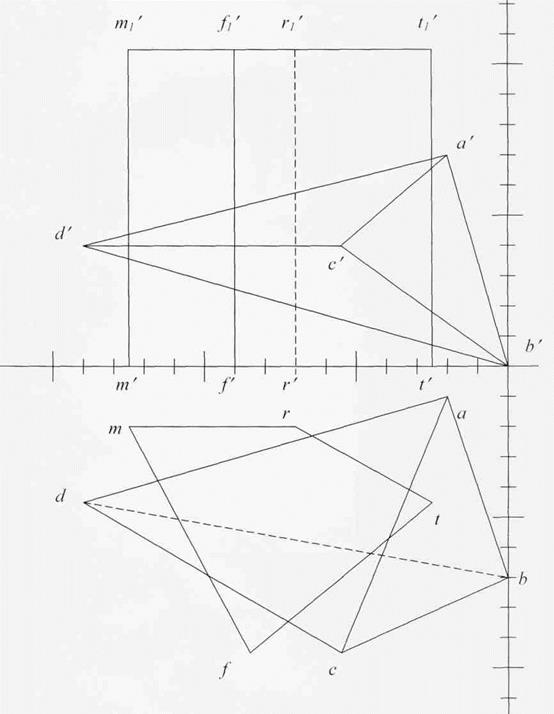 |
Рис. 51. Пересечение многогранников
- Построить линию пересечения пирамиды с прямой призмой.
- Определить видимость участков линии пересечения.
Раздел II. ЧЕРЧЕНИЕ

