Взаимное расположение прямых

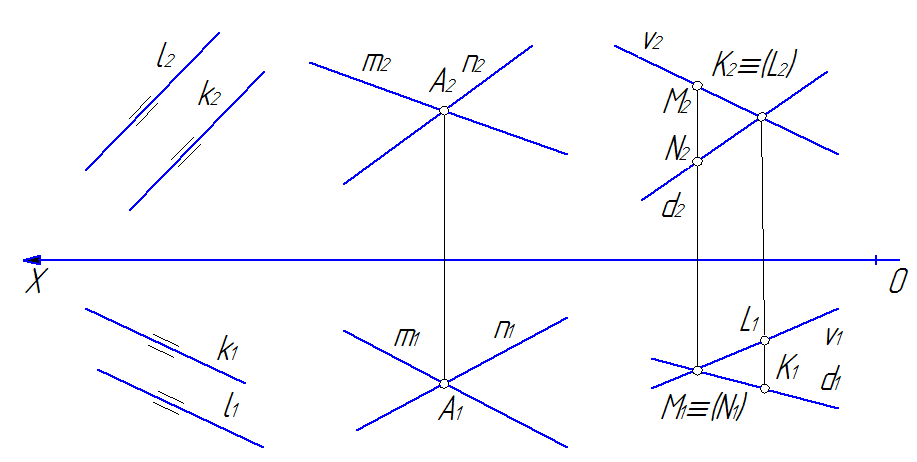
Прямые в пространстве относительно друг друга могут располагаться тремя способами (рис. 35): быть взаимно параллельными (l∥k); пересекаться (m∩n=A); скрещиваться (v∸d).

а) б) в)

Рис. 35

Если прямые общего положения взаимно параллельны, то на основании инварианта параллельности прямых следует признак параллельности прямых по эпюру (рис. 350а): одноимённые проекции прямых на всех плоскостях проекций будут взаимно параллельны.

Если прямые пересекаются, то на основании инварианта точки пересе­чения двух линий следует признак по эпюру (рис. 35б): точки пересечения одноимённых проекций прямых лежат на общих линиях связи.

Если прямые скрещиваются, то на эпюре (рис. 35в): точке пересечения одноимённых проекций прямых на одной плоскости проекций соответствуют проекции двух разных точек на другой плоскости проекций. Например, общей точке M₁≡N₁ пересечения горизонтальных проекций прямых соответствуют разные точки M₂Ìv₂ и N₂Ìd₂ на фронтальной плоскости проекций.

2.5. Способы задание плоскости на эпюре

Плоскость на эпюре может быть задана шестью способами: тремя точками, не лежащими на одной прямой; прямой и точкой, не лежащей на прямой; двумя пересекающимися прямыми; двумя параллельными прямыми; плоской фигурой; следами.

На рис. 36 плоскость задана: тремя точками А, В и С (рис. 36а); точкой А и прямой l (рис. 36б); двумя пересекающимися прямыми l и k (рис. 36в); двумя параллельными прямыми l и k (рис. 36г); плоской фигурой – ∆АВС (рис. 36г). Эти способы задания плоскости уже знакомы еще со школьной программы. Рассмотрим более подробней способ задания плоскости ее следами (рис. 37).

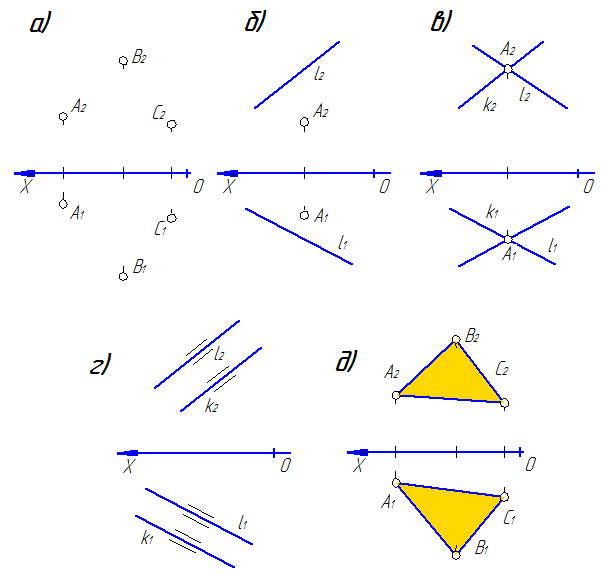
Рис. 36

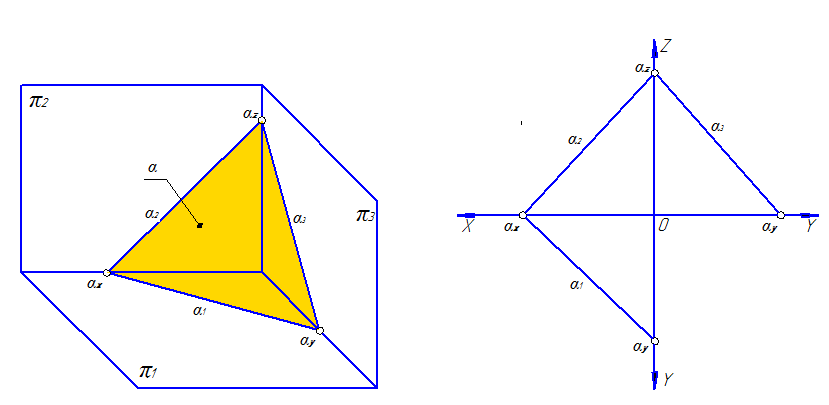
Рис. 37

Линия пересечения плоскости a с плоскостью проекций называется следом данной плоскости. На рис. 37 обозначено:

– a∩π₁ = a₁ – горизонтальный след плоскости a, a₁Ì π₁;

– a∩π₂= a₂ – фронтальный след плоскости a, a₂Ì π₂;

– aÌπ₃= a₃ – профильный след плоскости a, a₃Ì π₃.

Точки пересечения плоскости a с осями проекций называются точками схода следов: a∩0Х=a_х, a∩0Y=a_y, a∩0Z=a_z.

Следует помнить, что при решении задач по начертательной геометрии можно переходить от одного способа задания плоскости к другому т.к. они взаимозаменяемы.

Характеристика плоскостей

Все плоскости пространства подразделяются на плоскости общего и частного положений.

Плоскости общего положения. Плоскости не перпендикулярные ни к одной из плоскостей проекций называются плоскостями общего положения. Примеры изображения таких плоскостей приведены на рис. 36 и 37.

Плоскости частного положения. Плоскости перпендикулярные и параллельные плоскостям проекций относятся к плоскостям частного положения.

Проецирующие плоскости. Плоскости перпендикулярные к одной из плоскостей проекций называются проецирующими плоскостями. Характер­ным признаком таких плоскостей на эпюре является то что одна из ее проекций вырождается в прямую.

Плоскость перпендикулярная плоскости π₁ называются горизонтально-проецирующей плоскостью (рис. 38). Характерным признаком такой плоскости является то, что ее горизонтальная проекция вырождается в прямую. Кроме того, следует отметить, что угол между вырожденной проекцией плоскости и осью 0Х есть угол наклона проецирующей плоскости к фронтальной плоскости проекций (β).

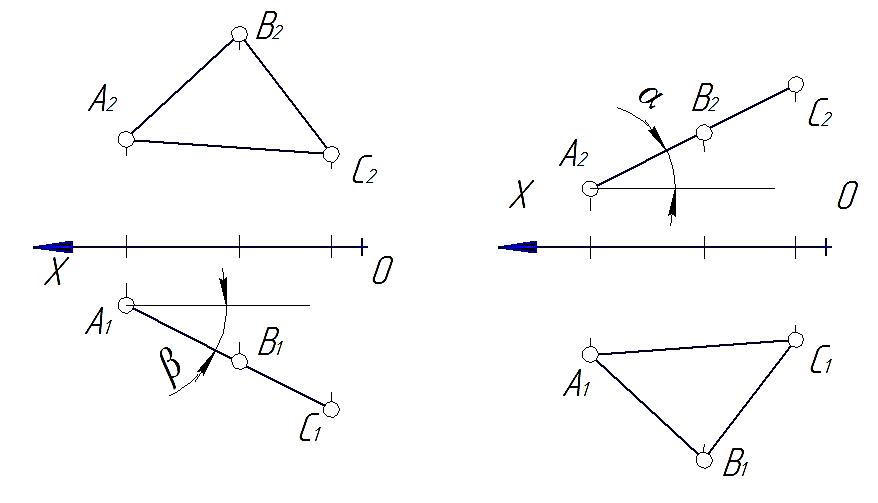
Рис. 38 Рис. 39

Плоскость перпендикулярная плоскости π₂ называются фронтально-проецирующей плоскостью (рис. 39). Характерным признаком такой плоскости является то, что ее фронтальная проекция вырождается в прямую. Кроме того, следует отметить, что угол между вырожденной проекцией плоскости и осью 0Х есть угол наклона проецирующей плоскости к горизонтальной плоскости проекций (α).

Плоскости уровней. Плоскости параллельные плоскостям проекций называются плоскостями уровней (рис. 40, 41).

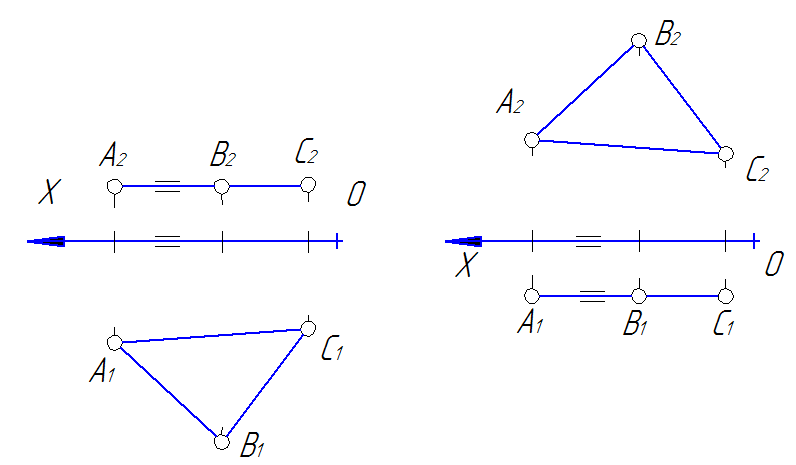
Рис. 40 Рис. 41

Плоскость параллельная плоскости π₁ называются горизонтальной плоскостью уровня (рис. 40). Характерным признаком такой плоскости является то, что ее фронтальная проекция вырождается в прямую параллельную оси 0Х. Кроме того, следует отметить, что геометрические фигуры, принадлежащие такой плоскостям на горизонтальную плоскость проекций, проецируются в натуральную величину.

Плоскость параллельная плоскости π₂ называются фронтальной плоскостью уровня (рис. 41). Характерным признаком такой плоскостей является то, что ее горизонтальная проекция вырождается в прямую параллельную оси 0Х. Кроме того, следует отметить, что геометрические фигуры, принадлежащие такой плоскости на фронтальную плоскость проекций, проецируются в натуральную величину.

2.7. Контрольные вопросы

1. Как получается эпюр прямой?

2. Какие прямые относятся к прямым частного положения?

3. Какие прямые называют линиями уровня?

4. Что такое горизонталь? Характерный признак и особенности изобра­жения горизонтали на эпюре Монжа?

5. Что такое фронталь? Характерный признак и особенности изображе­ния фронтали на эпюре Монжа?

6. Какая прямая называется профильной прямой? Характерный признак и особенности изображения профильной прямой на эпюре Монжа?

7. Какие прямые называются проецирующими?

8. Как называются прямые перпендикулярные плоскостям проекций π₁,π₂и π₃? Характерный признак и особенности изображения этих прямых эпюре Монжа?

9. Что такое следы прямой и как они определяются?

10. Как находится натуральная величина длинны отрезка и угол наклона этого отрезка к плоскости проекций?

11. Как производится деление отрезка в заданном соотношение?

12. Характерные признаки определения взаимного расположения пря­мых по эпюру Монжа (пересечение, параллельность, скрещиваемость)?

13. Сформулируйте теорему о проецировании прямого угла пересекающихся прямых.

14. Сформулируйте условия о проецировании прямого угла двух скре­щивающихся прямых.

15. Перечислите и покажите на примерах способы задания на эпюре плоскости общего положения.

16. Какие плоскости относятся к плоскостям частного положения?

17. Покажите на эпюре характерные признаки и особенности горизон­тально-проецирующей и фронтально-проецирующей плоскостей.

18. Какие плоскости относятся к плоскостям уровней?

19. Покажите на эпюре характерные признаки и особенности горизон­тальных и фронтальных плоскостей уровней.