Заполнение сводных таблиц: Метод проекций. Способы проецирования. Ортогональное проецирование.

Теоретические свойства построения чертежа в инженерной графике базируются на правилах построения изображений, основанных на методе проекций. Изображение объектов трехмерного пространства на плоскости получают методом проецирования.

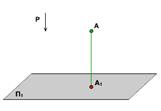
Проецирование – это процесс, в результате которого получают изображения, представляющие собой проекции на плоскости.

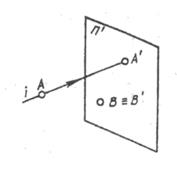Аппарат проецирования:

- точки А, В;

- проецирующие лучи i;

- плоскость проекции п'

Процесс проецирования заключается в проведении проецирующих лучей через заданные точки до встречи с плоскостью проекций. Точка пересечения проецирующего луча с плоскостью проекций и определяет проекцию этой точки. Так, проекцией точки А является точка А'.Проекцией точки В является точка В', хотя проекция точки В, лежащей в плоскости п', совпала с самой точкой. Чтобы получить проекцию какой-либо фигуры, необходимо построить проекции ее характерных точек и соединить их на чертеже соответствующими линиями.

В основу построения объекта на плоскости положен метод проекций. Проецирование – это построение объекта на плоскости при помощи проецирующих лучей, исходящих из точки. Плоскость, на которую падают лучи – проецирующая плоскость.

Способы проецирования
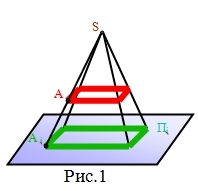
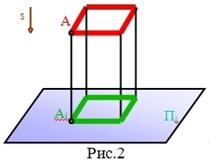
I.Центральное проецирование: проецирующие лучи выходят из одной точки (центра). Размеры предмета на плоскости проекций искажаются (рис.1).	II.Параллельное проецирование: проецирующие лучи параллельны и составляют с плоскостью угол 90 градусов (прямоугольное проецирование или ортогональное рис.2) и угол отличный от 90 градусов (косоугольное проецирование рис.3).

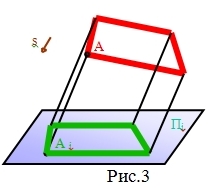Ортогональное проецирование – это частный случай параллельного проецирования. При ортогональном проецировании проецирующие лучи перпендикулярны к плоскости проекций.

Ортогональное проецирование обеспечивает простоту геометрических построений при определении ортогональных проекций точек, а также возможность сохранять на проекциях размеры проецируемой фигуры.

Практическое занятие № 14

Выполнение заданий в рабочей тетради: Метод Монжа.

Образование чертежа точки в системе двух и трех плоскостей проекций

Данный метод позволяет определить место каждой точки изображения относительно других точек.

Точку (предмет) помещают в систему двух взаимоперпендикулярных плоскостей, которые используются в качестве плоскостей проекций.

П1 - горизонтальная плоскость проекций;

П2 - фронтальная плоскость проекций;

х - ось проекций

А1 - горизонтальная проекция точки А,

А2 - фронтальная проекция точки А.

Если даны проекции А1 и А2 некоторой точки А, то проведя перпендикуляры: через т.А1 к плоскости П1, а через т. А2 к П2, получим в пересечении этих прямых определенную точку А (рис.5).

Вращением вокруг оси ОX плоскость П1 совместим с плоскостью П2. При этом проекции А2 и А1 точки А расположатся на одном перпендикуляре к оси проекций - на линии связи.

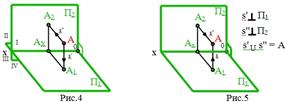В результате указанного совмещения плоскостей П2 и П1 получается чертеж, известный под названием эпюр Монжа или двухкартинный чертеж, включающий две взаимосвязанные проекции - “картины”.

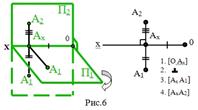
Известно, что чертежи сложных конструкций содержат не две, а большее число изображений - проекций. Рассмотрим введение в систему П1, П2 еще одной плоскости проекций, перпендикулярной П1 и П2 (рис.7).

П3 - профильная плоскость проекций.

Опустим перпендикуляр на плоскость П3 из точки А и получим.

А3 - профильную проекцию точки А (рис.8).

Для получения трехкартинного чертежа точки надо повернуть плоскость П1 вокруг оси x и плоскость П3 вокруг оси z до совмещения их с плоскостью П2 (рис.9).

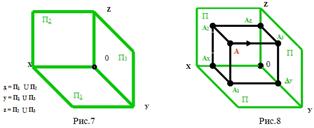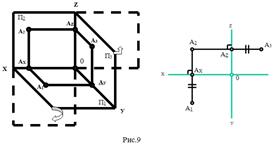Вывод: Каждая точка пространства характеризуется тремя координатами: А (х, у, z).

Задание: Построить в рабочей тетради комплексный чертеж точки А (17;13;25)

Практическое занятие № 15