Прогнозирование жилищного кредитования

§1.Прогнозирование жилищного кредитования в России.

Проведем прогноз по объему предоставленных кредитов и определим сколько триллионов рублей будет предоставлено кредитов в России в IV квартале 2016 года. Рассмотрим данные за три года (2014, 2015 и 2016) по кварталам. В табл. 5. приводятся данные об объемах предоставленных кредитов (в трил. руб.).

Таблица 5

Объем предоставленных кредитов (в трил. руб.).

Квартал/ год	I	II	III	IV
	1,67	1,50	2,84	4,25
	2,04	0,91	1,70	2,66
	1,44	1,33	2,36

Рассчитаем трендовую и сезонную компоненту и сделаем прогноз ожидаемого объема предоставленных кредитов на IV квартал 2016 г.

Разумно предположить, что объем кредитов в текущем квартале зависит от объема кредитов предыдущих кварталов.

Определим коэффициент корреляции между рядами y_t и y_t-k и измерим тесноту связи между объёмами текущего и предыдущих кварталов.

Коэффициент автокорреляции со смещением на k периодов находится по формуле:

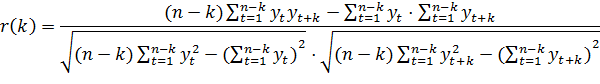
Рассчитаем коэффициент автокорреляции со смещением на 1 квартал.

Для расчетов используем данные табл. 6.

Таблица 6

t	yt	yt+1	yt2	yt+12	yt*yt+1
	1,67	1,5	2,79	2,25	2,51
	1,5	2,84	2,25	8,07	4,26
	2,84	4,25	8,07	18,06	12,07
	4,25	2,04	18,06	4,16	8,67
	2,04	0,91	4,16	0,82	1,86
	0,91	1,7	0,83	2,89	1,55
	1,7	2,66	2,89	7,08	4,52
	2,66	1,44	7,08	2,07	3,83
	1,44	1,33	2,07	1,77	1,92
	1,33	2,36	1,77	5,57	3,14
Итого	20,34	21,03	49,96	52,7455	44,31

Таким образом, коэффициент автокорреляции первого порядка равен:

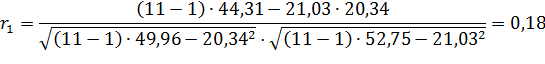
Рассчитаем коэффициент автокорреляции со смещением на 2 квартала. Для этого составим расчетную табл. 7.

Таблица 7

t	yt	yt+2	yt2	yt+22	yt*yt+2
	1,67	2,84	2,79	8,07	4,74
	1,5	4,25	2,25	18,06	6,38
	2,84	2,04	8,07	4,16	5,79
t	yt	yt+2	yt2	yt+22	yt*yt+2
	4,25	0,91	18,06	0,83	3,87
	2,04	1,7	4,16	2,89	3,47
	0,91	2,66	0,83	7,08	2,42
	1,7	1,44	2,89	2,07	2,45
	2,66	1,33	7,08	1,77	3,54
	1,44	2,36	2,07	5,57	3,40
Итого:	19,01	19,53	48,20	50,50	36,05

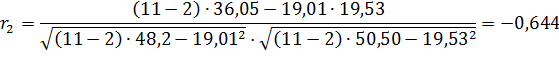
Рассчитаем коэффициент автокорреляции со смещением на 3 квартала. Для этого составим расчетную табл. 8.

Таблица 8

t	yt	yt+3	yt2	yt+32	yt*yt+3
	1,67	4,25	2,79	18,06	7,10
	1,5	2,04	2,25	4,16	3,06
	2,84	0,91	8,07	0,83	2,58
	4,25	1,7	18,06	2,89	7,23
	2,04	2,66	4,16	7,08	5,43
	0,91	1,44	0,83	2,07	1,31
	1,7	1,33	2,89	1,77	2,26
	2,66	2,36	7,08	5,57	6,28
Итого:	17,57	16,69	46,12	42,43	35,24

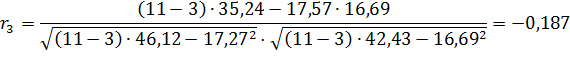
Рассчитаем коэффициент автокорреляции со смещением на 4 квартала. Для этого составим расчетную табл. 9.

Таблица 9

t	yt	yt+4	yt2	yt+42	yt*yt+4
	1,67	2,04	2,79	4,16	3,41
	1,5	0,91	2,25	0,83	1,37
	2,84	1,7	8,07	2,89	4,83
	4,25	2,66	18,06	7,08	11,31
	2,04	1,44	4,16	2,07	2,94
	0,91	1,33	0,83	1,77	1,21
	1,7	2,36	2,89	5,57	4,01
Итого:	14,91	12,44	39,05	24,37	29,06

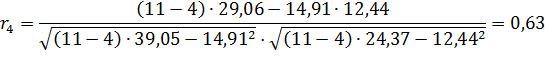
Таким образом, коэффициенты автокорреляции временного ряда:

Порядок
Коэффициент автокорреляции	0,180	–0,644	–0,187	0,63

Построим коррелограмму для исходного временного ряда (рис. 3).

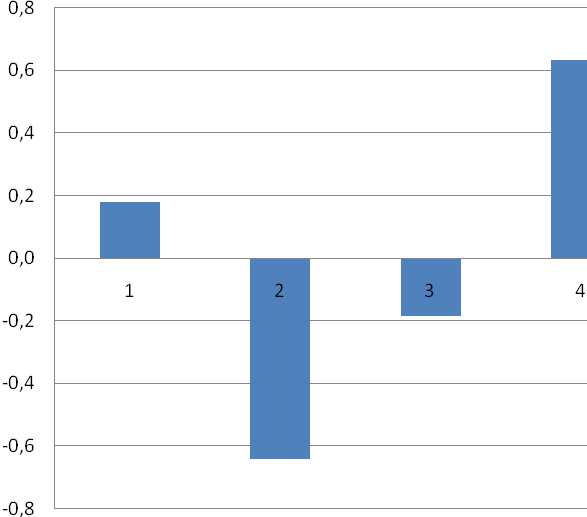
Рис. 3. Коррелограмма временного ряда

Проверим значимость всей группы коэффициентов автокорреляции с помощью Q-критерия Бокса-Пирса.

Наблюдаемое значение Q-статистики равно

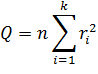
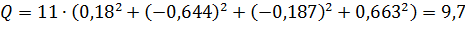
Критическое значение для уровня значимости α=0,05 и числа степеней свободы k=4 находим по таблице критических точек распределения

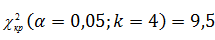
Так как Q ≥ 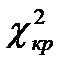, то в группа коэффициентов считается значимой.

Построим график наблюдаемых значений временного ряда (рис. 4).

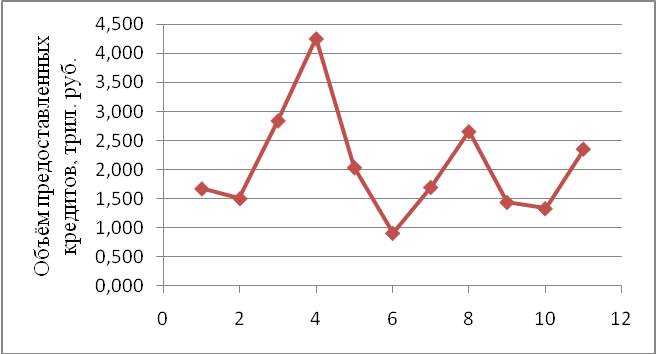
Рис. 4. График наблюдаемых значений временного ряда

По графику наглядно видно наличие убывающей тенденции.

Наиболее высоким оказался коэффициент автокорреляции 4-го порядка, тогда ряд содержит циклические колебания с периодом в 4 квартала (τ=4). Поскольку амплитуда колебания непостоянна, то построим мультипликативную модель временного ряда.

Проведем выравнивание исходных уровней ряда методом двойной скользящей средней. Для этого:

а) просуммируем уровни ряда последовательно за каждые 4 квартала со сдвигом на один момент времени и определим условные годовые объемы предоставленных кредитов (гр. 3 табл. 10);

б) разделив полученные суммы на 4, найдем скользящие средние за 4 квартала - тренд скользящих средних (гр. 4 табл. 10). Отметим, что полученные таким образом выровненные значения уже не содержат сезонной компоненты;

в) приведем эти значения в соответствии с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние. Центрированная средняя и есть значение рассчитанного тренда (гр. 4 табл. 10).

г) найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 10).

Таблица 10

Выравнивание исходных уровней ряда

Время, кварталы	Временной ряд	Условные годовые объёмы	Скользящая средняя за 4 квартала Т(4)	Центрированная скользящая средняя Т	Оценка сезонной компоненты
	1,670
	1,502	10,267	2,567
	2,842	10,632	2,658	9,956	2,489
	4,253	10,036	2,509	9,212	2,303
	2,035	8,889	2,222	8,227	2,057
	0,906	7,291	1,823	7,497	1,874
	1,695	6,693	1,673	7,219	1,805
	2,655	7,116	1,779	5,396	1,349
	1,437	7,776	1,944	3,723	0,931
	1,329
	2,355

Используем эти оценки для расчета значений сезонной компоненты S (табл. 11). Для этого найдем средние за каждый показатель оценки сезонной компоненты S_i.

Таблица 11

Поиск сезонной компоненты

Показатели	Кварталы
Год				1,088	1,646
	0,860	0,448	0,970	1,538
	0,772
Итого за i-ый квартал (за все годы)	1,632	1,777	4,413	3,185
Средняя оценка сезонной компоненты для i-го квартала,	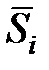0,816	0,448	1,029	1,592
Скорректированная сезонная компонента, Si	0,840	0,461	1,059	1,639

В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем годам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4. Для данной модели имеем:

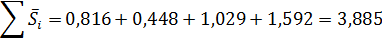
Определим корректирующий коэффициент:

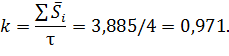
Определим скорректированные значения сезонной компоненты, умножив ее средние оценки на корректирующий коэффициент k.

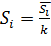, где i=1,2,3,4.

Проверим условие равенства суммы значений сезонной компоненты:

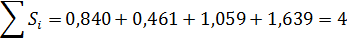
Получим следующие значения сезонной компоненты:

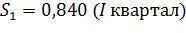
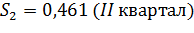
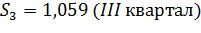
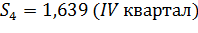
Занесем полученные значения в табл. 12 для соответствующих месяцев каждого показателя (гр. 3).

Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. Тем самым мы получим величины T×E=Y:S (гр. 4 табл. 12), которые содержат только тенденцию и случайную компоненту.

Таблица 12

Расчет выровненных значений Т и ошибок Е в мультипликативной модели

t	yt	Si	T∙E=yt/Si		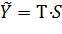E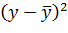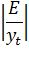
1	2	3	4	5	6	7	8
	1,67	0,840	1,988			0,153
	1,5	0,461	3,257			0,314
	2,84	1,059	2,683	2,612	0,074	0,608	0,026
	4,25	1,639	2,594	2,583	0,018	4,803	0,004
	2,04	0,840	2,422	2,366	0,047	0,001	0,023
	0,91	0,461	1,964	2,023	-0,027	1,336	0,030
	1,7	1,059	1,600	1,748	-0,156	0,134	0,092
	2,66	1,639	1,620	1,726	-0,175	0,352	0,066
	1,44	0,840	1,710	1,862	-0,127	0,390	0,089
	1,33	0,461	2,883			0,537
	2,36	1,059	2,223			0,086
Сумма:	-0,345	0,080	0,330

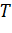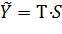Найдем значения уровней ряда, полученные по мультипликативной модели. Для этого прибавим к уровням Т значения сезонной компоненты для соответствующих кварталов. Графически значения и представлены на рис. 5.

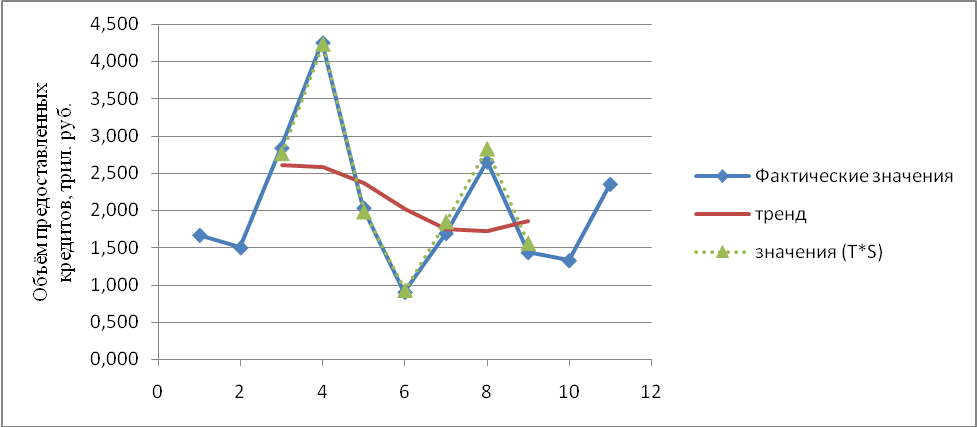
Рис. 5. Объем предоставляемых кредитов в России (фактические и выравненные по мультипликативной модели значений уровней ряда)

Абсолютные ошибки в мультипликативной модели определяются как

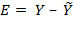
Численные значения ошибки приведены в гр. 6 табл. 12.

В данной модели сумма квадратов абсолютных ошибок составляет 0,080 (см. гр. 6 табл. 12). Общая сумма квадратов отклонений фактических уровней этого ряда от среднего значения равна 8,715 (см. гр. 7 табл. 12). Таким образом, коэффициент детерминации:

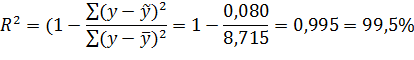
то есть 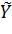на 99,5% близок к фактическим данным.

Сумма модуля отношения абсолютных ошибок к фактическим уровням этого ряда равна 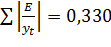(см. гр. 8 табл. 11). Средняя ошибка аппроксимации равна:

,

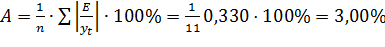Модель качественна, так как 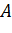не превышает 10%.

.

Проведем прогноз ожидаемого объема предоставленных кредитов на IV квартал 2016 г., то есть 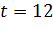. Для этого умножим значение объема предоставленных кредитов IV квартала 2015 г.( 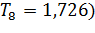на сезонную компоненту IV квартала :

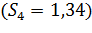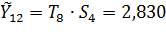
Таким образом, объем предоставленных кредитов в IV квартале 2016 г. составит 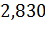триллионов рублей.

§2.Прогнозирование жилищного кредитования в Чувашской республике.

Проведем прогноз по объему предоставленных кредитов и определим, сколько триллионов рублей будет предоставлено кредитов в Чувашской республике в IV квартале 2016 года. Рассмотрим данные за три года (2014, 2015 и 2016) по кварталам. В табл. 13 приводятся данные об объемах предоставленных кредитов (в трил. руб.).

Таблица 13

Объем предоставленных кредитов (в трил. руб.)

Квартал/ год	I	II	III	IV
	0,016	0,015	0,023	0,033
	0,021	0,008	0,016	0,027
	0,015	0,014	0,024

Рассчитаем трендовую и сезонную компоненту и сделаем прогноз ожидаемого объема предоставленных кредитов на IV квартал 2016 г.

Разумно предположить, что объем кредитов в текущем квартале зависит от объема кредитов предыдущих кварталов.

Определим коэффициент корреляции между рядами y_t и y_t-k и измерим тесноту связи между объёмами текущего и предыдущих кварталов.

Коэффициент автокорреляции со смещением на k периодов находится по формуле:

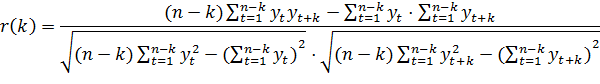
Рассчитаем коэффициент автокорреляции со смещением на 1 квартал.

Для расчетов используем данные табл. 14.

Таблица 14

t	yt	yt+1	yt2	yt+12	yt*yt+1
	0,0164	0,0152	0,0003	0,0002	0,0003
	0,0152	0,0230	0,0002	0,0005	0,0004
	0,0230	0,0330	0,0005	0,0011	0,0008
	0,0330	0,0212	0,0011	0,0004	0,0007
	0,0212	0,0083	0,0004	0,0001	0,0002
t	yt	yt+1	yt2	yt+12	yt*yt+1
	0,0083	0,0160	0,0001	0,0003	0,0001
	0,0160	0,0267	0,0003	0,0007	0,0004
	0,0267	0,0148	0,0007	0,0002	0,0004
	0,0148	0,0138	0,0002	0,0002	0,0002
	0,0138	0,0238	0,0002	0,0006	0,0003
Итого	0,1885	0,1959	0,0040	0,0043	0,0037

Таким образом, коэффициент автокорреляции первого порядка равен:

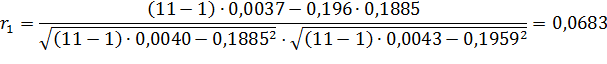
Рассчитаем коэффициент автокорреляции со смещением на 2 квартала. Для этого составим расчетную табл. 15.

Таблица 15

t	yt	yt+2	yt2	yt+22	yt*yt+2
	0,0164	0,0230	0,0003	0,0005	0,0004
	0,0152	0,0330	0,0002	0,0011	0,0005
	0,0230	0,0212	0,0005	0,0004	0,0005
	0,0330	0,0083	0,0011	0,0001	0,0003
	0,0212	0,0160	0,0004	0,0003	0,0003
	0,0083	0,0267	0,0001	0,0007	0,0002
	0,0160	0,0148	0,0003	0,0002	0,0002
	0,0267	0,0138	0,0007	0,0002	0,0004
	0,0148	0,0238	0,0002	0,0006	0,0004
Итого:	0,1747	0,1807	0,0038	0,0041	0,0032

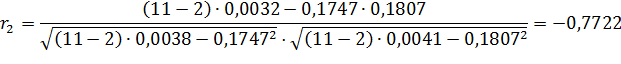
Рассчитаем коэффициент автокорреляции со смещением на 3 квартала. Для этого составим расчетную табл. 16.

Таблица 16

t	yt	yt+3	yt2	yt+32	yt*yt+3
	0,0164	0,0330	0,0003	0,0011	0,0005
	0,0152	0,0212	0,0002	0,0004	0,0003
	0,0230	0,0083	0,0005	0,0001	0,0002
t	yt	yt+3	yt2	yt+32	yt*yt+3
	0,0330	0,0160	0,0011	0,0003	0,0005
	0,0212	0,0267	0,0004	0,0007	0,0006
	0,0083	0,0148	0,0001	0,0002	0,0001
	0,0160	0,0138	0,0003	0,0002	0,0002
	0,0267	0,0238	0,0007	0,0006	0,0006
Итого:	0,1599	0,1577	0,0036	0,0036	0,0031

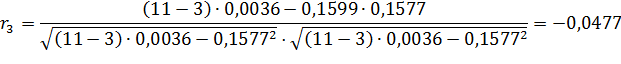
Рассчитаем коэффициент автокорреляции со смещением на 4 квартала. Для этого составим расчетную табл. 17.

Таблица 17

t	yt	yt+4	yt2	yt+42	yt*yt+4
	0,0164	0,0212	0,0003	0,0004	0,0003
	0,0152	0,0083	0,0002	0,0001	0,0001
	0,0230	0,0160	0,0005	0,0003	0,0004
	0,0330	0,0267	0,0011	0,0007	0,0009
	0,0212	0,0148	0,0004	0,0002	0,0003
	0,0083	0,0138	0,0001	0,0002	0,0001
	0,0160	0,0238	0,0003	0,0006	0,0004
Итого:	0,1331	0,1247	0,0029	0,0025	0,0025

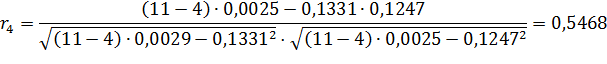
Таким образом, коэффициенты автокорреляции временного ряда:

Порядок
Коэффициент автокорреляции	0,0683	–0,7722	–0,0477	0,5468

Построим коррелограмму для исходного временного ряда (рис. 6).

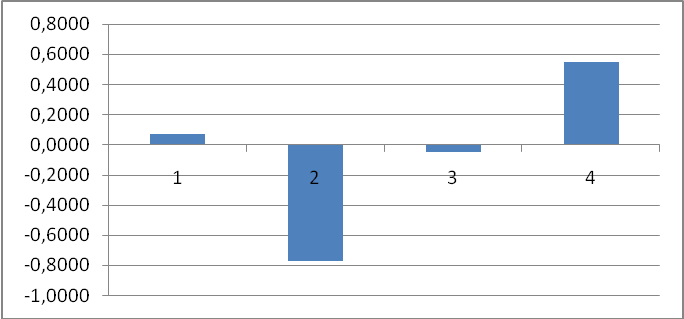
Рис. 6. Коррелограмма временного ряда

Проверим значимость всей группы коэффициентов автокорреляции с помощью Q-критерия Бокса-Пирса.

Наблюдаемое значение Q-статистики равно

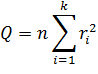
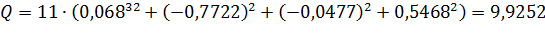
Критическое значение для уровня значимости α=0,05 и числа степеней свободы k=4 находим по таблице критических точек распределения

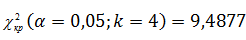
Так как Q ≥ 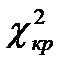, то в группа коэффициентов считается значимой.

Построим график наблюдаемых значений временного ряда (рис. 7).

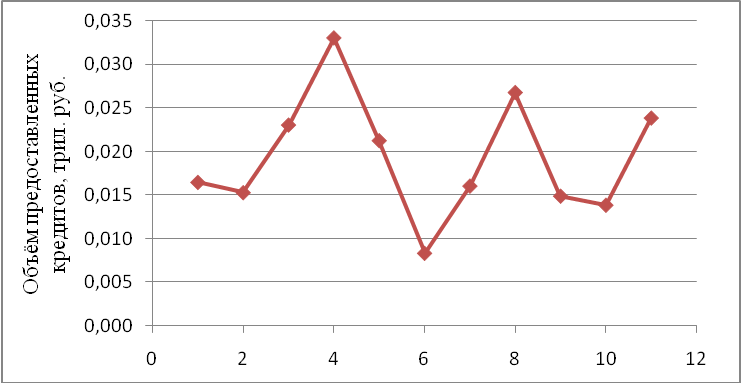
Рис. 7. График наблюдаемых значений временного ряда

По графику наглядно видно наличие убывающей тенденции.

Наиболее высоким оказался коэффициент автокорреляции 4-го порядка, тогда ряд содержит циклические колебания с периодом в 4 квартала (τ=4). Поскольку амплитуда колебания непостоянна, то построим мультипликативную модель временного ряда.

Проведем выравнивание исходных уровней ряда методом двойной скользящей средней. Для этого:

а) просуммируем уровни ряда последовательно за каждые 4 квартала со сдвигом на один момент времени и определим условные годовые объемы предоставленных кредитов (гр. 3 табл. 18);

б) разделив полученные суммы на 4, найдем скользящие средние за 4 квартала - тренд скользящих средних (гр. 4 табл. 18). Отметим, что полученные таким образом выровненные значения уже не содержат сезонной компоненты;

в) приведем эти значения в соответствии с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние. Центрированная средняя и есть значение рассчитанного тренда (гр. 4 табл. 18).

г) найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 18).

Таблица 18

Выравнивание исходных уровней ряда

методом двойной скользящей средней

Время, кварталы	Временной ряд	Условные годовые объёмы	Скользящая средняя за 4 квартала Т(4)	Центрированная скользящая средняя Т	Оценка сезонной компоненты
	0,016
	0,015
	0,023	0,088	0,022
	0,033	0,092	0,023	0,023	1,022
Время, кварталы	Временной ряд	Условные годовые объёмы	Скользящая средняя за 4 квартала Т(4)	Центрированная скользящая средняя Т	Оценка сезонной компоненты
	0,021	0,085	0,021	0,022	1,484
	0,008	0,078	0,020	0,020	1,035
	0,016	0,072	0,018	0,019	0,440
	0,027	0,066	0,016	0,017	0,927
	0,015	0,071	0,018	0,017	1,559
	0,014
	0,024

Используем эти оценки для расчета значений сезонной компоненты S (табл. 19). Для этого найдем средние за каждый показатель оценки сезонной компоненты S_i.

Таблица 19

Расчета значений сезонной компоненты S

Показатели	Кварталы
Год				1,022	1,484
	1,035	0,440	0,927	1,559
	0,788
Итого за i-ый квартал (за все годы)	1,823	0,440	1,949	6,043
Средняя оценка сезонной компоненты для i-го квартала,	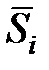0,912	0,440	0,974	1,521
Скорректированная сезонная компонента, Si	0,948	0,457	1,013	1,582

В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем годам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4. Для данной модели имеем:

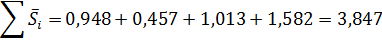
Определим корректирующий коэффициент:

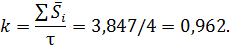
Определим скорректированные значения сезонной компоненты, умножив ее средние оценки на корректирующий коэффициент k.

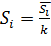, где i=1,2,3,4.

Получим следующие значения сезонной компоненты:

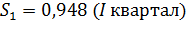
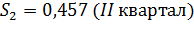
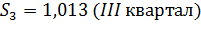
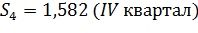
Проверим условие равенства 4 суммы значений сезонной компоненты:

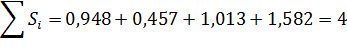
Занесем полученные значения в табл. 20 для соответствующих месяцев каждого показателя (гр. 3).

Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. Тем самым мы получим величины T×E=Y:S (гр. 4 табл. 20), которые содержат только тенденцию и случайную компоненту.

Таблица 20

Расчет выровненных значений Т и ошибок Е в мультипликативной модели

t	yt	Si	T∙E=yt/Si		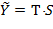E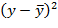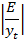
1	2	3	4	5	6	7	8
	0,016	0,948	0,017			0,00001
	0,015	0,457	0,033			0,00002
	0,023	1,013	0,023	0,023	0,0002	0,00001	0,008
	0,033	1,582	0,021	0,035	-0,002	0,00019	0,066
	0,021	0,948	0,022	0,019	0,002	0,00000	0,084
	0,008	0,457	0,018	0,009	0,000	0,00012	0,040
	0,016	1,013	0,016	0,017	-0,001	0,00001	0,093
	0,027	1,582	0,017	0,027	0,000	0,00006	0,015
	0,015	0,948	0,016	0,018	-0,003	0,00002	0,202
	0,014	0,457	0,030			0,00003
	0,024	1,013	0,023			0,00002
Сумма:	-0,005	0,00005	0,508

Найдем значения уровней ряда, полученные по мультипликативной модели. Для этого прибавим к уровням Т значения сезонной компоненты для соответствующих кварталов. Графически значения 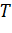и 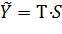представлены на рис. 8.

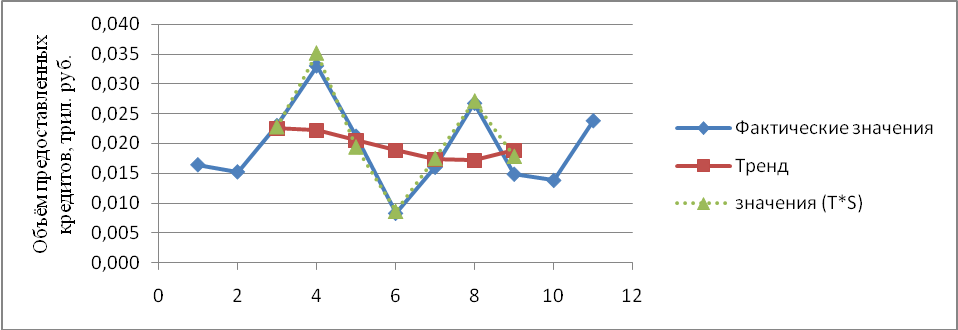
Рис. 8. Объем предоставляемых кредитов в Чувашской республике (фактические и выравненные по мультипликативной модели значений уровней ряда)

Абсолютные ошибки в мультипликативной модели определяются как

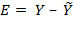
Численные значения ошибки приведены в гр. 6 табл. 20.

В данной модели сумма квадратов абсолютных ошибок составляет -0,005 . Общая сумма квадратов отклонений фактических уровней этого ряда от среднего значения равна 0,00005 (см. гр. 7 табл. 21). Таким образом, индекс корреляции:

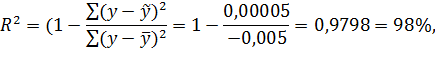
то есть 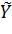на 98% близок к фактическим данным.

Сумма модуля отношения абсолютных ошибок к фактическим уровням этого ряда равна 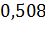(см. гр. 8 табл. 21). Средняя ошибка аппроксимации равна:

,

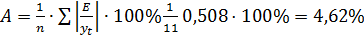Модель качественна, так как A не превышает 10%.

Проведем прогноз ожидаемого объема предоставленных кредитов на IV квартал 2016 г., то есть 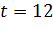. Для этого умножим значение объема предоставленных кредитов IV квартала 2015 г.( 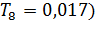на сезонную компоненту IV квартала :

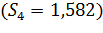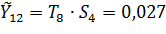
Таким образом, объем предоставленных кредитов в IV квартале 2016 г. составит 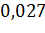триллион рублей, то есть около 27 миллиард рублей.

Заключение

В результате проведенного мною анализа необходимо отметить, что жилищное кредитование стремительно набирает свои обороты в развитии и внедрении в жизнь. Оно активно развивается и дает возможность семьям реализовать себя в своем будущем. Увеличение кредитных организаций во всех субъектах Российской Федерации свидетельствует о масштабе развития ипотеки. Но главной проблемой данного вида кредитования остается процентная ставка по кредитам. Еще в 2012 году в мае по указу президента была поставлена задача по снижению ставок по жилищным кредитам.[10]

В первой главе курсовой работы проведен анализ жилищного кредитования, предоставленных физическим лицам в течение пяти лет, помогают сделать определенного рода выводы.

Количество предоставленных кредитов с каждым годом увеличивается приблизительно на 80%. Следует также отметить, что средневзвешенная процентная ставка с каждым годом становится все меньше. Этот фактор положительно влияет на заинтересованность населения в жилищном кредитовании, так как низкая процентная ставка способствует снижению переплаты кредита.

Количество кредитных организаций возрастает с каждым годом. Они, безусловно, необходимы для предоставления своих услуг населению. Темпы открытия данных организаций имеют тенденцию к увеличению. Это способствует повышению спроса на предоставление ипотечных кредитов.

Увеличение кредитных организаций ведет к динамике возрастания выданных жилищных кредитов.

Данные о количестве предоставляемых жилищных кредитов на одного человека по каждому из восьми федеральных округов говорят о том, что потенциал выдачи кредитов возрастает ежегодно. Следует выделить, что количество жилищных кредитов возрастает в каждом федеральном округе, независимо от его расположения.

Количество выданных жилищных кредитов возрастает, однако и задолженность по ним также возрастает.

Выявленный темп роста нельзя рассматривать с положительной стороны, так как рассчитанные показатели отражают тенденцию роста задолженности.

Необходимо разработать проекты, в которых усовершенствуется программа ипотечного кредитования и любая семья сможет приобрести жилье без лишних сложностей. Ипотека должна быть простой и доступной.

Составил прогноз объема предоставленных кредитов на конец 2016 года (IV квартал) с помощью временного ряда, рассмотрев мультипликативную модель. Объем предоставленных кредитов на конец 2016 года составил в России 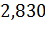трилллионов рублей, а в Чувашии 20 миллиард рублей, что показывает также увеличение по сравнению с другими кварталами предыдущих годов.

В работе построенная мультипликативная модель временного ряда с помощью двойной скользящей средней. В результате получил модели с аппроксимациям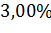и и 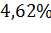, и коэффициентами корреляции равными 0.995 и 0.98 для России и Чувашской республики соответственно . Данные показатели дают сделать вывод о качестве построенных моделей.