Математические основы прогнозирования

§1.Временной ряд

Прогнозирование – это научное, основанное на системе установленных причинно-следственных связей и закономерностей, выявление состояния и вероятностных путей развития явлений и процессов.[7]

Статистические методы прогнозирования опираются на анализ временных рядов.

Временным рядом (рядом динамики) называется последовательность значений статистического показателя-признака, упорядоченная в хронологическом порядке, т.е. в порядке возрастания временного параметра. Отдельные наблюдения временного ряда называются уровнями этого ряда.⁶

Каждый временной ряд содержит два элемента:

1. значения времени;

2. соответствующие им значения уровней ряда.

В качестве показателей времени во временных рядах могут указываться либо определенные моменты времени, либо отдельные периоды (сутки, месяцы, кварталы, полугодия, годы и т.д.) в зависимости от характера временного параметра ряды делятся на моментные и интервальные.

В моментных рядах уровни характеризуют значения показателей по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значения показателя за определенные интервалы времени.

Уровни рядов динамики могут представлять собой абсолютные, относительные и средние величины. Если уровни ряда представляют собой непосредственно не наблюдаемые значения, а произвольные величины: средние или относительные, то такие ряды называются производными. Уровни этих рядов получаются с помощью некоторых вычислений на основе абсолютных показателей.

В самом общем виде временной ряд может быть представлен как комбинация тенденции, сезонных (периодических) колебаний, непериодических колебаний и случайной составляющей. Непериодические колебания, если они имеются, обычно имеют сложную природу, представляют собой комбинацию нескольких колебаний различной или даже переменной периодичности и переменного размаха. Для установления самого факта наличия непериодических колебаний, а тем более надежного определения их параметров требуются временные ряды большой длительности, редко встречающиеся на практике. Элементы непериодических колебаний, если они имеются, можно рассматривать как один из возможных компонентов случайной составляющей. В такой постановке задача прогнозирования по временному ряду сводится к определению параметров сезонных колебаний и тенденции и их последующему использованию для целей предсказания будущих значений временного ряда.

§2. Компоненты временного ряда

Тенденция или тренд - это долговременная закономерность изменения исследуемой величины во времени[8]. Сезонная компонентапредставляет собой периодические колебания, имеющие относительно стабильный период колебаний на протяжении достаточно длительного периода времени. Более точные результаты определения тенденции достигаются в случае если из исходного временного ряда уже удалены сезонные колебания.

В зависимости от характера сезонных колебаний различают два вида моделей – аддитивная и мультипликативная.

По аддитивной модели временной ряд с сезонными колебаниями представляется в виде:

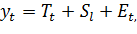
где 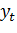– значение прогнозируемой переменной для 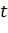-го момента времени;

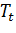-трендовая составляющая 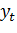; 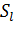- сезонная составляющая ;

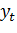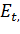- случайная ошибка.

По мультипликативной модели временной ряд с сезонными колебаниями имеет в вид:

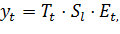
Для решения вопроса о том какая из рассматриваемых моделей должна быть выбрана для конкретного временного ряда, необходимо построить график изменения прогнозируемой величины во времени и проанализировать изменение амплитуды сезонных колебаний (Рис.1.). В случае если амплитуда сезонных колебаний не имеет ярко выраженной тенденции к изменению во времени, то тогда может быть выбрана аддитивная модель (a), в противном случае предпочтительна мультипликативная (б)

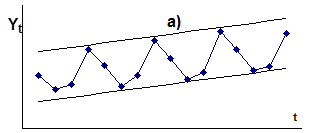
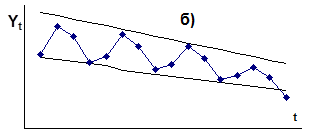
Рис 1. Временные ряды, характерные для аддитивной (а) и мультипликативной(б)моделей.

При обработке временных рядов необходимо учитывать наличие автокорреляции, при котором значения последующего уровня ряда зависят от предыдущих значений.

Автокорреляция – явление взаимосвязи между рядами: первоначальным и этим же рядом сдвинутым относительно первоначального положения на 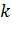моментов времени.

Формула для расчета коэффициента автокорреляции имеет вид:

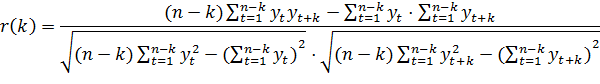
1. Если наибольшим по модулю значением автокорреляции является автокорреляция первого порядка, то временной ряд состоит из тренда и случайной компоненты.

2. Если наибольшим является 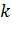-ый коэффициент автокорреляции, то временной ряд содержит длину периода сезонных колебаний, равную .

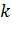§3. Сглаживание временного ряда

Аналитическое выравнивание временного ряда (сглаживание) – способ моделирования тенденции временного ряда: построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда.[9]

Длина периода сезонных колебаний – это число временных интервалов, через которые характер изменения временного ряда повторяется.

Экстраполяция – это метод научного исследования, который основан на распространении прошлых и настоящих тенденций, закономерностей, связей на будущее развитие объекта прогнозирования. К методам экстраполяции относятся метод скользящей средней, метод экспоненциального сглаживания, метод наименьших квадратов.

Сущность метода наименьших квадратов состоит в минимизации суммы квадратических отклонений между наблюдаемыми и расчетными величинами. Расчетные величины находятся по подобранному уравнению – уравнению регрессии. Чем меньше расстояние между фактическими значениями и расчетными, тем более точен прогноз, построенный на основе уравнения регрессии.

Теоретический анализ сущности изучаемого явления, изменение которого отображается временным рядом, служит основой для выбора кривой. Иногда принимаются во внимание соображения о характере роста уровней ряда. Так, если рост выпуска продукции ожидается в арифметической прогрессии, то сглаживание производится по прямой. Если же оказывается, что рост идет в геометрической прогрессии, то сглаживание надо производить по показательной функции.

Рабочая формула метода наименьших квадратов:

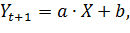
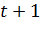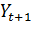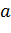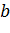где - прогнозный период; - прогнозируемый показатель; и - коэффициенты; 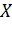- условное обозначение времени;

Расчет коэффициентов 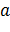и 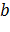осуществляется по следующим формулам:

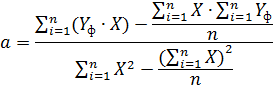
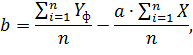
где 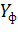- фактическое значение ряда динамики; n – число уровней временного ряда;

Сглаживание временных рядов методом наименьших квадратов служит для отражения закономерности развития изучаемого явления. В аналитическом выражении тренда время рассматривается как независимая переменная, а уровни ряда выступают как функция этой независимой переменной.

Развитие явления зависит не от того, сколько лет прошло с отправного момента, а от того, какие факторы влияли на его развитие, в каком направлении и с какой интенсивностью. Отсюда ясно, что развитие явления во времени выступает как результат действия этих факторов.

Правильно установить тип кривой, тип аналитической зависимости от времени – одна из самых сложных задач предпрогнозного анализа.

Подбор вида функции, описывающей тренд, параметры которой определяются методом наименьших квадратов, производится в большинстве случаев эмпирически, путем построения ряда функций и сравнения их между собой по величине среднеквадратической ошибки, вычисляемой по формуле:

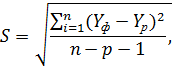
где 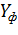– фактические значения ряда динамики; 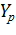– расчетные (сглаженные) значения ряда динамики; 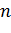– число уровней временного ряда; 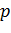– число параметров, определяемых в формулах, описывающих тренд (тенденцию развития).

Недостатки метода наименьших квадратов:

· при попытке описать изучаемое экономическое явление с помощью математического уравнения, прогноз будет точен для небольшого периода времени и уравнение регрессии следует пересчитывать по мере поступления новой информации;

• сложность подбора уравнения регрессии, которая разрешима при использовании типовых компьютерных программ.

Другим методом выравнивания (сглаживания) временного ряда, т. е. вьделения неслучайной составляюпцей, является метод скользящих средних.

Скользящая средняя – это переменная, значения которой равны среднему арифметическому значения исследуемой величины в точке для которой она вычисляется и значений всех точек, отстоящих от нее на 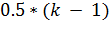слева и справа в случае если 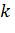нечетное и 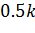– если 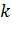четное. При вычислении значения скользящей средней для следующей точки временного ряда номера точек, участвующих в вычислении смещаются на единицу. Длина периода сезонных колебаний – это число временных интервалов, через которые характер изменения временного ряда повторяется.

Таким образом для их вычисления скользящей средней вначале необходимо определить длину периода сезонных колебаний 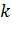. В простейшем случае найти ее можно на основании визуального анализа данных. Затем для каждой точки исходного временного ряда необходимо вычислить средние значения переменной 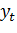. В случае если 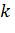четное, полученный ряд скользящих средних 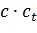оказывается смещенным относительно 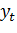на величину равную половине временного интервала. Значения скользящей средней при этом соответствуют уже не конкретным интервалам, например первому или второму интервалу, а второй половине интервала 1 и первой половине интервала 2 (рис. 2). Следующее значение скользящей средней соответствует половинам интервалов 2 и 3 и т.д. Смещенная на пол интервала скользящая средняя называется межинтервальной скользящей средней. Для устранения возникшего смещения полученные скользящие средние с любым четным периодом осреднения необходимо еще раз усреднить с периодом усреднения, равным двум. Полученная в результате повторного осреднения скользящая средняя называется центрированной скользящей средней.

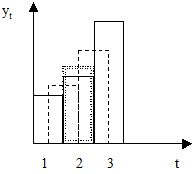
Рис. 2. Получение центрированных скользящих средних с периодом осреднения равным двум.

Где:

- значения yt;

- межинтервальные скользящие средние для точек 1-2 и 2-3 соответственно;

- интервальная скользящая средняя для точки 2.

Как видно из схемы расчетов в результате усреднения число значений скользящей средней оказывается меньше числа точек исходного временного ряда на величину равную периоду осреднения 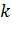так как на краях временного ряда отсутствуют точки необходимые для нахождения скользящей средней. Потеря 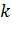точек приводит к тому, что минимальная длительность временного ряда должна быть равной хотя бы трем периодам колебаний.

Следующий методом сглаживания является метод экспоненциального сглаживания. Метод экспоненциального сглаживания наиболее эффективен при разработке среднесрочных прогнозов. Он приемлем при прогнозировании только на один период вперед. Его основные достоинства простота процедуры вычислений и возможность учета весов исходной информации. Рабочая формула метода экспоненциального сглаживания:

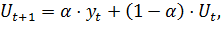
где 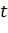– период, предшествующий прогнозному; 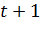– прогнозный период; 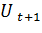- прогнозируемый показатель; α - параметр сглаживания; 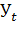- фактическое значение исследуемого показателя за период, предшествующий прогнозному; 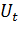- экспоненциально взвешенная средняя для периода, предшествующего прогнозному.

При прогнозировании данным методом возникает два затруднения:

• выбор значения параметра сглаживания ;
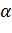• определение начального значения .

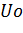От величины 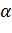зависит, как быстро снижается вес влияния предшествующих наблюдений. Чем больше 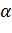, тем меньше сказывается влияние предшествующих лет. Если значение α близко к единице, то это приводит к учету при прогнозе в основном влияния лишь последних наблюдений. Если значение α близко к нулю, то веса, по которым взвешиваются уровни временного ряда, убывают медленно, т.е. при прогнозе учитываются все (или почти все) прошлые наблюдения.

Таким образом, если есть уверенность, что начальные условия, на основании которых разрабатывается прогноз, достоверны, следует использовать небольшую величину параметра сглаживания (α→0). Когда параметр сглаживания мал, то исследуемая функция ведет себя как средняя из большого числа прошлых уровней. Если нет достаточной уверенности в начальных условиях прогнозирования, то следует использовать большую величину α, что приведет к учету при прогнозе в основном влияния последних наблюдений.

Точного метода для выбора оптимальной величины параметра сглаживания α нет. В отдельных случаях автор данного метода профессор Браун предлагал определять величину α, исходя из длины интервала сглаживания. При этом α вычисляется по формуле:

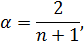
где 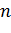– число наблюдений, входящих в интервал сглаживания.

Задача выбора Uo (экспоненциально взвешенного среднего начального) решается следующими способами:

· если есть данные о развитии явления в прошлом, то можно воспользоваться средней арифметической и приравнять к ней ;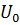

· если таких сведений нет, то в качестве 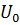используют исходное первое значение базы прогноза .

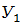Также можно воспользоваться экспертными оценками.

Отметим, что при изучении экономических временных рядов и прогнозировании экономических процессов метод экспоненциального сглаживания не всегда «срабатывает». Это обусловлено тем, что экономические временные ряды бывают слишком короткими (15-20 наблюдений), и в случае, когда темпы роста и прироста велики, данный метод не «успевает» отразить все изменения.