Задания для самостоятельной работы. 1. Допустим, что в двух кровеносных сосудах градиент давления одинаков
1. Допустим, что в двух кровеносных сосудах градиент давления одинаков, а поток крови (объемный расход) во втором сосуде на 80 % меньше, чем в первом. Найти отношение их диаметров.
Ответ:  .
.
2. Оценить минимально допустимое АД у жирафа, ниже которого кровоснабжение мозга становится невозможным. Мозг жирафа расположен на 3 м выше сердца.
Ответ: Р > 30 кПа.
3. Нормальное систолическое артериальное давление равно 120 мм рт. ст. Перевести это значение в единицы: а) атм; б) Па.
Ответ: Р = 0,16 атм.
4. Определить минимальное значение направленного вверх ускорения, которое вызывает у человека, с нормальной АД, нарушение кровоснабжение мозга.
Ответ: а=10 м/  .
.
5. Средняя скорость крови в аорте радиусом 1 см равна 30 см/с.
Выяснить, является ли данное течение ламинарным?
Ответ: число Рейнольдса меньше критического значения, поэтому течение будет ламинарным.
6. Определить максимальную массу крови, которая может пройти за 1 с через аорту при сохранении ламинарного характера течения. Диаметр аорты D = 2 см, а вязкость η = 4  .
.
Ответ: m=0,18 кг.
Физические основы гемодинамики. Основные понятия и формулы.
1. Условие неразрывности струи: 
2. При ламинарном течении жидкости произведение площади S сечения участка, через который она протекает, на ее скорость ʋ является постоянной величиной для данной трубки тока.
3. Уравнение Бернулли: 
где ρ - плотность идеальной жидкости; ʋ - скорость ее течения; Р- статическое давление; h - высота расположения центра выделенного сечения потока жидкости.
4. Формула Ньютона, определяющая силу  внутреннего трения в движущейся жидкости:
внутреннего трения в движущейся жидкости: 
где η - вязкость жидкости; S - площадь соприкосновения слоев движущейся жидкости;  - градиент скорости (скорость сдвига).
- градиент скорости (скорость сдвига).
5. Ньютоновская жидкость - жидкость, вязкость которой не зависит от градиента скорости. Неньютоновская жидкость - жидкость, вязкость которой зависит от градиента скорости и давления.
6. Формула Пуазейля: 
где V - объем вязкой жидкости, ламинарно протекающей по участку гладкой трубы длиной L и радиусом r за время t;  - давление соответственно в начале и конце выделенного участка.
- давление соответственно в начале и конце выделенного участка.
7. Формула Гагена - Пуазейля: 
где Q - объемная скорость жидкости; Х - гидравлическое сопротивление,

8. Число Рейнольдса: 
где d - диаметр трубы, по которой со скоростью ʋ течет жидкость плотностью  и вязкостью η.
и вязкостью η.
9. Формула Моенса - Кортевега: 
где ʋ - скорость распространения пульсовой волны; Е - модуль упругости стенок сосуда; h - толщина стенок сосуда; ρ - плотность жидкости в сосуде; d - диаметр сосуда.
Задачи.
1. При быстром подъеме в самолете человек ощущает щелчки в ушах. Это происходит в тот момент, когда давление за барабанной перепонкой уравнивается с наружным давлением. Если бы этого не происходило, то какая сила действовала бы на барабанную перепонку площадью 0,5  при подъеме на 1000 м?
при подъеме на 1000 м?
Решение
В первом приближении давление воздуха при подъеме убывает по закону
Р=  ,
,
ρ=1,29 кг/  - плотность воздуха у поверхности Земли.
- плотность воздуха у поверхности Земли.
 Па - давление атмосферы.
Па - давление атмосферы.
| 
 /
/  )
)  Па,
Па,
F=  =12 500
=12 500  = 0,63 Н.
= 0,63 Н.
Ответ: F= 0,63 Н.
2. Нормальное систолическое артериальное давление равно 120 мм рт. ст. Перевести это значение в единицы: а) атм; б) Па.
Решение
1 мм рт. ст. = ρgh = 132,6 
1 атм = 760 мм рт. ст. = 101 кПа;
120 мм рт. ст. = 120 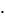 133=16 000 Па = 0,16 атм.
133=16 000 Па = 0,16 атм.
Ответ: Р = 16 000 Па = 0,16 атм.
3. Какова должна быть высота столба жидкости в капельнице, чтобы лекарство поступало в вену под избыточным давлением 60 мм рт. ст.? Давление в вене на 18 мм рт. ст. выше атмосферного. При какой высоте остаточного столба в трубке поступление препарата плотностью ρ=1 г/  прекратится?
прекратится?
Решение
При вливаниях через капельницу лекарство поступает в вену за счет гидростатического давления жидкости.
 .
.
 мм рт. ст. = 10 400 Па.
мм рт. ст. = 10 400 Па.
 .
.
Лекарство перестает поступать в вену, когда его давление уравняется с давлением в ней:  мм рт. ст. = 2400 Па.
мм рт. ст. = 2400 Па.
 = 0,25 м.
= 0,25 м.
Ответ: а)  . б)
. б)  = 0,25 м.
= 0,25 м.
4. При каждом сокращении сердце прокачивает примерно 70  крови под средним давлением 105 мм рт. ст. Рассчитать мощность сердца при частоте сокращений n=70 ударов в минуту.
крови под средним давлением 105 мм рт. ст. Рассчитать мощность сердца при частоте сокращений n=70 ударов в минуту.
Решение
Работа, совершаемая при одном сокращении, находится по формуле: 
Р=105  133 = 14 000 Па;
133 = 14 000 Па;  = 70
= 70  ;
;  Дж.
Дж.
Работа за 1 мин: А=n  Дж.
Дж.
Это средняя мощность.
Мощность в течение систолы (  ) больше, так как длительность систолы
) больше, так как длительность систолы  времени сердечного цикла.
времени сердечного цикла.  Вт.
Вт.
Ответ: N=1,17 Вт;  =3,9 Вт.
=3,9 Вт.
5. Вода течет по горизонтальной трубе переменного сечения. Скорость течения воды в широкой части, в горизонтально расположенной трубе переменного сечения, переменного  разность статических давлений в широкой и узкой части трубы ∆Р = Р1 – Р2 =1,82 кПа, Определите скорость
разность статических давлений в широкой и узкой части трубы ∆Р = Р1 – Р2 =1,82 кПа, Определите скорость  течения воды в узкой части трубы.
течения воды в узкой части трубы.
Решение. Обозначим ρ - плотность воды, запишем уравнение Бернулли для данного случая:  /2 + Р2 =
/2 + Р2 =  / 2 + Р1 ,
/ 2 + Р1 ,
Выразим из него искомую величину  :
: 
Подставив в полученную формулу численные значения входящих в нее величин, получим  .
.
Ответ:  .
.
6. По артерии диаметром d=4 мм течет кровь со скоростью ʋ=0,4 м/с. Определите кинетическую энергию минутного объема крови.
Решение.
Искомая кинетическая энергия (Е) определяется по формул: 
где m- масса крови в минутном объеме V, m = ρV = ρQt = ρSʋt, здесь ρ = 1,05  - плотность крови; Q = Sʋ - объемная скорость крови;
- плотность крови; Q = Sʋ - объемная скорость крови;  - площадь сечения сосуда; t = 60 с - время
- площадь сечения сосуда; t = 60 с - время
Таким образом, искомая величина рассчитывается по формуле

Ответ: 0,025 Дж.
7. Скорость пульсовой волны в некоторой артерии ʋ=10 м/с. Чему равен модуль упругости Е этого сосуда, если диаметр d просвета сосуда в 9 раз больше толщины его стенки? Плотность ρ жидкости в сосуде считайте равной плотности воды.
Решение. Из формулы Моенса - Кортевега выразим искомую величину и подставим численные значения: 

Ответ: 0.81 МПа.
8. На участке артерии длиной L=1 см и диаметром d=4 мм гидравлическое сопротивление кровотоку Х = 8  Па
Па 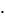 (с/
(с/  ). Каково значение вязкости крови η на этом участке сосуда?
). Каково значение вязкости крови η на этом участке сосуда?
Решение. Преобразование формулы для гидравлического сопротивления позволяет сразу получить необходимое выражение для расчета вязкости крови:

Ответ: 5 мПа 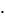 с.
с.
